理想気液混合物（理想気体-ファンデルワールス流体混合物）の相図を概観したわけですが、 露点、泡点という視点から進んで、 相分離の結果生じた露や泡がどのように成長していくのかに注目してみると、 また興味深い現象が見えてきます。 １成分の流体では、 温度を上げて液体から泡が生じた（沸騰が始まった）時、 さらに加熱すると泡は大きくなり（蒸発が進み）、 最終、すべてが泡、蒸気になります。 けれども２成分系では、 泡が温度を上げるとともに消失してしまうことがあります （逆行蒸発 retrograde vaporization）。 ここでは理想気液混合物における逆行蒸発・凝縮現象について見てみます。
逆行蒸発 retrograde vaporization は、 温度を下げる方向で考えると逆行凝縮 retrograde condensation ということになります。 逆行凝縮現象は塩化メチル CH3Cl と二酸化炭素 CO2 の混合物の臨界温度付近の圧縮挙動に関わって、 100 年以上前Kuenen によって見出されました。 通常、逆行凝縮・逆行蒸発という言葉は、圧力変化にかかわって語られますが、 ここでは温度変化の場合も含めて使っています。
|
|
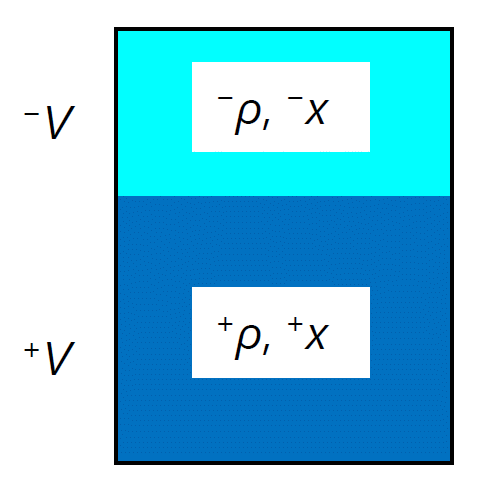
| 図 X-1. 流体混合物の気液相分離。 |
２相分離が起きた時の両相への成分の分配について、 「てこの法則」はよく知られています。 通常、てこの法則は組成比を一定に保った状態で、 圧力一定の条件で温度を上げていったときに、 両相にどれだけの物質量 \(n\) が分配されるかを問題にします。 理想気体-ファンデルワールス流体混合物の場合には、 相間の物質量比より、体積比に注目した方が見通しがよくなります。
理想気体 X -ファンデルワールス流体 A 混合物で相分離が生じているとき、 全体の体積 \(V\) の内、 蒸気相の占める体積を \({}^- V\)、 液相の占める体積を \({}^+ V\) とすると（\(V = {}^- V + {}^+ V\)）、 総体として見た時の密度 \(\rho\) と理想気体成分 X のモル分率 \(x\) について次の関係が成り立ちます：
\begin{equation} n_\mrm{X} = x V \rho = {}^- V {}^-\rho_\mrm{X} + {}^+ V {}^+\rho_\mrm{X} = V \rho_\mrm{X} \label{eq:total_mfrax} \end{equation}
\begin{equation} n_\mrm{A} = (1 - x) V \rho = {}^- V {}^-\rho_\mrm{A} + {}^+ V {}^+\rho_\mrm{A} \label{eq:total_mfraa} \end{equation}
気液両相で X の密度は等しく、理想気体成分 X の量的関係 \eqref{eq:total_mfrax} からは 気液の量比についての制約はありません。 一方ファンデルワールス流体成分 A の量的関係 \eqref{eq:total_mfraa} からは、 気液共存状態での A の密度が、理想気体成分の密度に依存せず、 純粋な A の気液共存状態での密度（\({}^\pm \rho^\star\)）に等しいので、 総体として見た時の密度 \(\rho\) と モル分率 \(x\) について次の関係が得られます：
\begin{equation} (1-x) \rho = (1 - {}^+ r) {}^-\rho^\star + {}^+ r {}^+\rho^\star \label{eq:total_mfra1} \end{equation}
ここで \({}^+ r\) は液相の体積比 \({}^+ V/V\)（\(= 1 - {}^- V/V\)）です。 液相の体積比 \({}^+ r\) に注目すると、式 \eqref{eq:total_mfra1} から次式を得ます：
\begin{equation} {}^+ r = \frac{(1-x) \rho - {}^-\rho^\star}{{}^+\rho^\star - {}^-\rho^\star} = \frac{\rho_\mrm{A} - {}^-\rho^\star}{{}^+\rho^\star - {}^-\rho^\star} \left(= \frac{\rho - {}^-\rho}{{}^+\rho - {}^-\rho} \right) \label{eq:vlratio} \end{equation}
つまり理想気液混合物では体積比について「てこの法則」が成り立ち、 気液の体積比は、蒸気相・液相の飽和密度との密度差の逆比になっているわけです。
混合流体の気液両相への分配比は、 化学的な操作においても大事なポイントになります。 たとえば実験室的なバッチ式の蒸留では、 温度を上げながら、液相の比率が 100 % の状態で蒸気相を取り除きつつ（留出させて）、 成分の分離・精製を行う操作を考えます（「単蒸留」simple distillation）。 こうした物質の出入り、全組成の変化をともなうような、 気液両相への分配の様相の変化も興味のあるところですが、 ここでは圧力・組成を一定に保った時の気液両相の量比に注目します。
|
| 図 X-2. 理想気体成分 X のモル分率 \(x\) = 0.5 の場合の 理想気体 X -ファンデルワールス流体 A 混合物の圧力 \(P\) - 温度 \(T\) 面の露点・泡点曲線。 露点曲線は水色で、泡点曲線は青で示しています。 図中、赤線は臨界線 critical line で \(x\) = 0.5 の場合の臨界圧力は 11/81 = 0.1350... です。 圧力 \(P\) = 0.15 で温度を変化させた場合（図中の緑の線）、泡点曲線と２度交わります。 |
先に理想気液混合物の \((P, T) \)図の議論の中でも指摘したように、 理想気液混合物では１成分のファンデルワールス流体では見られない、 少し変わった挙動が現れます。 図 X-2 には理想気体成分 X のモル分率 \(x\) = 0.5 における泡点・露点曲線の挙動を示しました。 理想気体成分のモル分率 \(x\) = 0.5 の場合、圧力 \(P\) = 0.15 で温度を上げていくと（図の緑の線）、 温度 \(T\) = 0.1961... と 0.2944... で泡点（沸点）を通過します。 つまり \(T\) = 0.196 で液体が沸騰して気液共存状態になった後、 さらに温度を上げると今度は蒸気の凝縮が起きるようになり \(T\) = 0.294 で液体にもどるわけです。 この温度を上げて蒸気が凝縮するという現象を（広い意味で）逆行蒸発 retrograde evaporation と呼びます。
モル分率・圧力を一定に保ったまま温度を上げた時の、 気液共存状態での液相の体積比 \({}^+ r\) の変化を求めることを考えてみましょう。 これには式 \eqref{eq:vlratio} でファンデルワールス流体成分 A の全密度 \(\rho_\mrm{A}\) を求めればよいわけですが、 気液共存状態で先にも見た次式が成り立つことに注意します：
\begin{equation} P = {}^{\pm}P^{\star}(T) + \rho_\mrm{X} T \label{eq:mix_coex0} \end{equation}
ここから気液共存状態でのファンデルワールス流体成分 A の全密度が、 次式で求められることになります：
\begin{equation} \rho_\mrm{A} = \frac{1-x}{x} \rho_\mrm{X} = \frac{1-x}{x} \frac{P - {}^{\pm}P^\star(T)}{T} \label{eq:dens_mix} \end{equation}
この式 \eqref{eq:dens_mix} を用いて、 気液共存状態をも含めた理想気液混合物の \((T, \rho_\mrm{A})\) 面の等圧線を描くことができます。 図 X-3 に示すのは、理想気体成分のモル分率 x = 0.5 の場合の等圧線図です。 等圧線の実線部分は１相の状態で状態方程式から得られ、 点線の部分は気液共存状態です （\(\rho_\mrm{A}\) を \(T\) の関数として得るわけです）。 圧力 \(P\) が純ファンデルワールス流体の蒸気圧 \({}^{\pm}P^\star(T)\) より十分高ければ（\({}^{\pm}P^\star(T) \lt P^\star_\mrm{C} = 1/27\)）、 ファンデルワールス流体成分の全密度 \(\rho_\mrm{A}\) は \(1/T\) に比例するようになります：
\begin{equation} \rho_\mrm{A} \approx \frac{1-x}{x} \frac{P}{T} ~~~~~~~~ (P \gg {}^{\pm}P^\star(T)) \label{eq:dens_mix1} \end{equation}
純ファンデルワールス流体の \((T, \rho_\mrm{A})\) 面の等圧線図では、 露点と泡点は同じ等圧線上にあり、 温度・圧力を決めただけでは密度 \(\rho_\mrm{A}\)（あるいは気液の量比）は決まりません。 また臨界圧力の等圧線は臨界点で相線と接し、 臨界圧力以上では気液の相分離は起きません。 けれどもモル分率を定めた理想気液混合物では、 温度・圧力を決めると密度 \(\rho_\mrm{A}\) が定まり、 その温度における純ファンデルワールス流体の飽和密度から気液の量比が決まります（式 \eqref{eq:vlratio}）。 また臨界圧力（\(x\) = 0.5 では 11/81）の等圧線は臨界点で相線と交わり、 気液の相分離が起きます。 そして臨界圧力より圧力の高い等圧線では泡点曲線と２度交わる、逆行蒸発・凝縮挙動が現れます。 そしてさらに圧力を上げ \(P\) = 0.171... で等圧線は泡点曲線と接し、 それ以上では気液の相分離は起きなくなります。
図 X-4 にはモル分率 \(x\) = 0.5 の気液共存状態の理想気液混合物の液相の体積比 \({}^+ r\) が、 種々の圧力で温度とともにどのように変化するかを示しました。 圧力が臨界圧力 \(P_\mrm{C}\)（\(x\) = 0.5 では 11/81 = 0.1358...）では、 臨界温度 \(T_\mrm{C}\)（= 8/27 = 0.296...）で液相の体積比 \({}^+ r\) は 1/2 になって気液共存状態が解消します （臨界点近傍では \(\rho_\mrm{A} \approx ({}^+\rho_\mrm{A} + {}^-\rho_\mrm{A})/2\) です）。 臨界圧力以下では通常みられるように、温度を上げるにつれて蒸発が進み液相が減っていき、 最終すべてが蒸気相になります。 しかし臨界圧力以上では温度を上げるにつれて最初は蒸発が進み液相が減っていくのですが、 途中で凝縮が起きるようになって液相の体積比は増加に転じ（逆行蒸発）、 最終すべてが液相になります。
|
|
| 図 X-3. ２相分離状態の理想気体-ファンデルワールス流体混合物を 等圧的に加熱した時の密度変化と気液分離。 理想気体成分のモル分率 \(x = 0.5\) で臨界全密度 \(\rho_\mrm{C}\) は 2/3 です。 等圧線は圧力 \(P\) = 0.171... で泡点曲線と接し、 それ以上の圧力では気液分離は生じません。 | 図 X-4. ２相分離状態の理想気体-ファンデルワールス流体混合物（理想気体のモル分率 \(x\) = 0.5）を 等圧的に加熱した時の、液相の体積比 \({}^+ r\) の温度変化。 臨界圧力 \(P_\mrm{C}\)（= 11/81 = 0.1358...）以上で、逆行蒸発現象が現れます。 |
実際の実験操作に照らすと、全物質量（\(n_\mrm{A} + n_\mrm{X}\)）と圧力が一定で、 体積が可変の状態を想定した方が、逆行蒸発・凝縮挙動をイメージしやすいかもしれません。 図 X-5 には圧力 \(P\) = 0.15 で理想気体成分 X のモル分率 \(x\) = 0.5 の場合の 理想気液混合物のモル体積 \(v\)（\(= \rho^{-1} = V/(n_\mrm{A} + n_\mrm{X})\)） の温度変化を示しました。 温度を上げていくと \(T\) = 0.196... で蒸気の生成が始まり、 \(T\) = 0.28 で蒸気相の比率が減少に転じ、 0.294... で蒸気相が消失します。
もし温度上昇にともなう蒸気の生成がなければ（１相のままならば）、 モル体積は図中の点線のように推移したはずです。 それが気液分離が起き泡（蒸気相）が大きくなっていく中で体積増加が加速します。 この時、蒸発して液相の体積が減りそうなものですが、 蒸発が起きる中、液相の体積も増加を続けます。 そして温度の上昇にともない液相の体積の増加が加速し、 最終、蒸気相は液相に呑み込まれて消失することになります。
気液両相の成分組成の観点から見てみると、 図 X-6 のような変化が見られます。 温度を上げるとともに蒸気相中の理想気体成分 X のモル分率 \(x\) は単調に減少していきます。 一方液相中の理想気体成分は最初減少しますが、 途中で減少が止まり増加に転じ、 最終、仕込みのモル分率 \(x\) = 0.5 になって気液分離が解消します。 この液相中の理想気体成分のモル分率の挙動も、 実験室の大気圧下の混合液体の蒸発では、 ちょっと想像できないものになっています。
|
|
| 図 X-5. 逆行蒸発・凝縮の起きる状況での下での、 圧力一定条件での理想気液混合物のモル体積（\(v = \rho^{-1}\)）の温度変化（黒い実線）。 青い実線は液相の体積（\({}^+ v = {}^+ r v\)）。 圧力 \(P\) = 0.15、理想気体成分 X のモル分率 \(x\) = 0.5 。 0.196 < \(T\) < 0.294 の温度域で気液分離が生じます。 | 図 X-6. ２相分離状態の理想気体-ファンデルワールス流体混合物（理想気体のモル分率 \(x\) = 0.5）を 圧力 \(P\) = 0.15 で加熱した時の、 理想気体成分 X の蒸気相のモル分率 \({}^-x\) と液相のモル分率 \({}^+x\)の温度変化。 |