
|
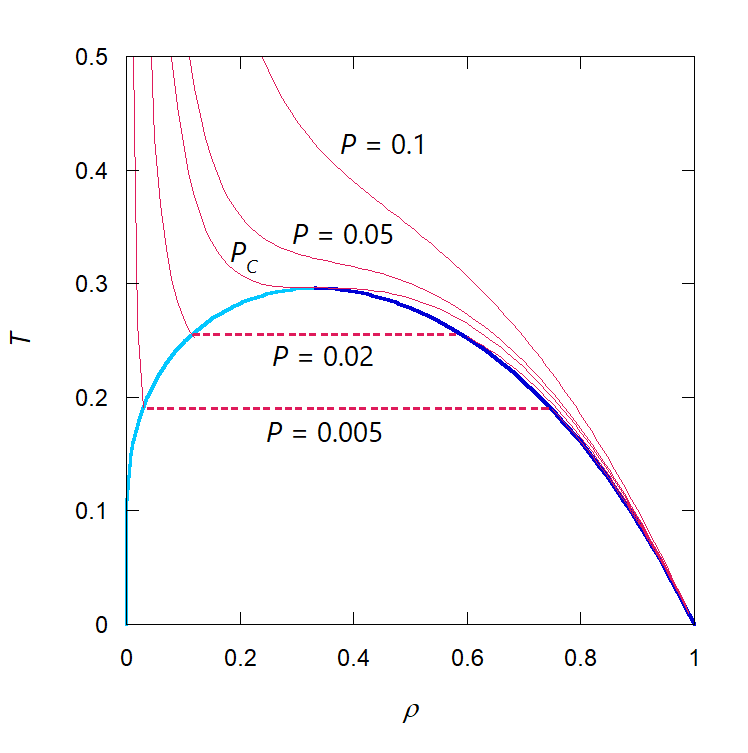
| 図 2-1. 純粋なファンデルワールス流体(\(x = 0\))の温度 \(T\) - 密度 \(\rho\)の飽和密度線図。 蒸気相の密度は水色で、液相の密度は青で示しています。 図中、赤線は等圧線で、 赤い点線は気液の共存状態を示します。 臨界圧力以上では蒸発・凝縮現象は生じません。 |
混合物の話の前に、まず純粋なファンデルワールス流体(\(x = 0\))の相挙動について見ておきましょう。 詳細はファンデルワールス流体のページを見ていただければよいのですが、 ここでは温度 \(T\) - 密度 \(\rho\) 面でのファンデルワールス流体の等圧線の挙動を、 図 2-1 に示しておきます。
圧力 \(P\) = 0.005 で、液体の温度を上げていくと、 流体は膨張して温度 \(T\) 0.19、密度 \(\rho\) 0.74 で泡点(沸点)に達し、 気化して密度 0.03 の蒸気になります。 圧力を高くして \(P\) = 0.02 では (液相の圧縮率が小さく等圧線は \(P\) = 0.005 の場合とほとんど重なっていますが) 温度 \(T\) 0.26、密度 \(\rho\) 0.59 で泡点(沸点)に達し、 気化して密度 0.12 の蒸気になります。 このように、圧力が高くになるにつれ気液の密度差は小さくなり、 最終、臨界圧力 \(P_\mrm{C}\) では気液の密度差はなくなり、 これ以上の圧力では気液の相分離は生じなくなります。
このファンデルワールス流体で気液の区別のなくなるぎりぎりの条件、 臨界温度 \(T_\mrm{C}\)、臨界圧力 \(P_\mrm{C}\)、臨界密度 \(\rho_\mrm{C}\) は 以下のようになります:
\begin{equation} \begin{aligned} T^\star_\mrm{C} &= 8/27 = 0.296296 \ldots \\ P^\star_\mrm{C} &= 1/27 = 0.037037 \ldots \\ \rho^\star_\mrm{C} &= 1/3 = 0.333 \ldots \end{aligned} \label{eq:vdw_critparam} \end{equation}
ここで記号の右肩の \(\star\) は、 純粋なファンデルワールス流体 A(\(x = 0\))のものであることを示すものとします。
|
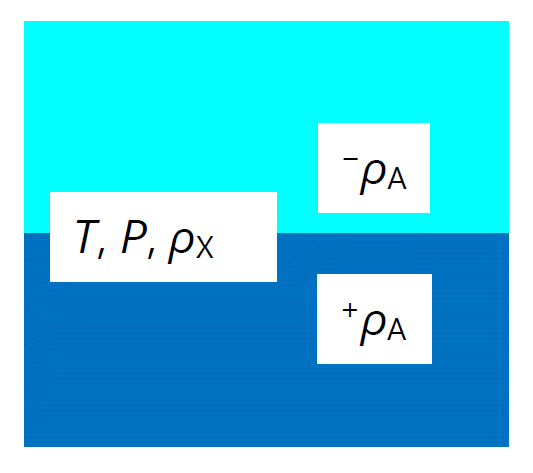
| 図 2-2. 理想気体 X -ファンデルワールス流体 A 混合物の気液平衡状態。 理想気体成分 X の密度は、蒸気相(水色)と液相(青)で同じです。 |
理想気体-ファンデルワールス流体混合物で相分離が生じた時、 凝縮・蒸発するのはファンデルワールス流体成分 A だけであって、 理想気体成分 X は蒸気相でも液相でも A とは無関係に存在します。 ですから理想気体-ファンデルワールス流体混合物での相分離は純ファンデルワールス流体と同様、 気液の相分離しか起きません。 水と油で見られるような液液分離などは起きず、 気液2相分離だけを考慮すればよいのです。 「理想気液混合物」と呼ぶのにふさわしいモデルであり、 このおはなしでは特に断らない限り、 理想気液混合物は理想気体-ファンデルワールス流体混合物であるとします。
理想気体-ファンデルワールス流体混合物の気液2相共存状態を特徴づける熱力学変数として、 温度 \(T\)、圧力 \(P\) と理想気体成分 X とファンデルワールス流体成分 A の 気液両相での密度 \({}^\pm \rho_\mrm{X}\)、\({}^\pm \rho_\mrm{A}\) の 6 つがあります。 相律から自由度は 2(成分の数 - 相の数 + 2)です。 ラウールの法則は温度 \(T\) と液相の組成比から圧力を与え、 密度は状態方程式からが決まるということになっています。 理想気体-ファンデルワールス流体混合物については、 温度 \(T\) (あるいは圧力 \(P\))と理想気体成分の密度 \(\rho_\mrm{X}\) を与えることで、気液の共存状態の熱力学変数を定めることができます。
気液2相共存状態で理想気体成分 X の密度は両相で等しく、 気液両相の A の密度と圧力について次式が成立します:
|
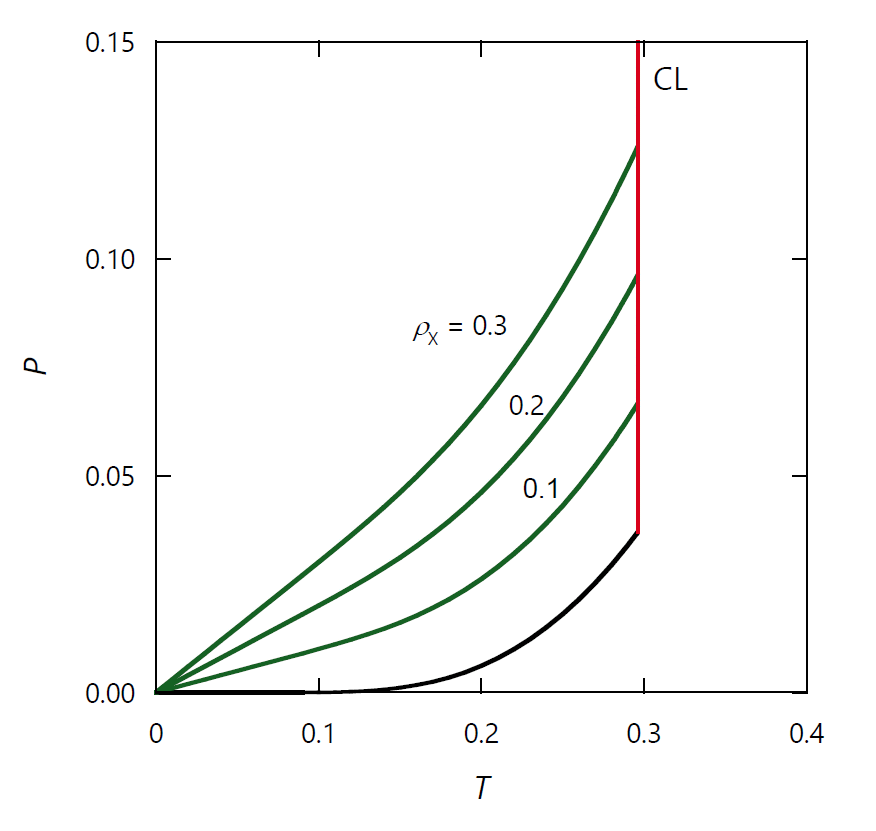
| 図 2-3. 理想気体成分 X の密度 \(\rho_\mrm{X}\) を変えた時の、 理想気体 X -ファンデルワールス流体 A 混合物の蒸気圧(凝縮圧)曲線。 図中、赤線は臨界線 CL。 |
\begin{equation} {}^{\pm} \rho_\mrm{A}(T, \rho_\mrm{X}) = {}^{\pm} \rho_\mrm{A}(T, \rho_\mrm{X}=0) \equiv {}^{\pm} \rho^\star(T) \label{eq:mix_coex0} \end{equation}
\begin{equation} {}^{\pm} P(T, \rho_\mrm{X}) = {}^{\pm}P^{\star}(T) + \rho_\mrm{X} T \label{eq:mix_coex1} \end{equation}
ここで記号の左肩に付している 複号 ± は、「複号同順」に従い、液相、蒸気相それぞれについて等式が成立することを示すものとします (\({}^+ \rho^\star (T) \gt {}^- \rho^\star (T)\) に注意)。 この関係から \((T, \rho_\mrm{X})\) における、気液共存状態の圧力と密度 \(({}^\pm P, {}^\pm \rho_\mrm{A})\) が決まることになります。
混合流体の気液の臨界状態は、 共存する気液両相の密度・組成が一致するようになる状態ですが、 純成分の場合と違い「点」ではなく「線」になり、 臨界線あるいは臨界軌跡 critical locus と呼ばれます。 今回の理想気体成分 X を含む場合、臨界パラメーターは X の密度の関数として、 次式のように表されます:
\begin{equation} \begin{aligned} T_\mrm{C}(\rho_\mrm{X}) &= T^\star_\mrm{C} = \frac{8}{27} \\ P_\mrm{C}(\rho_\mrm{X}) &= P^\star_\mrm{C} + \rho_\mrm{X} T^\star_\mrm{C} = \frac{1}{27} + \frac{8}{27} \rho_\mrm{X} \\ \rho_\mrm{C, A}(\rho_\mrm{X}) &= \rho^\star_\mrm{C} = \frac{1}{3} \end{aligned} \label{eq:mix_critparam} \end{equation}
図 2-3 には、理想気体成分 X の密度 \(\rho_\mrm{X}\) を変えた時の、 理想気体 X -ファンデルワールス流体 A 混合物の蒸気圧(凝縮圧)曲線の様子を示しました。 理想気体成分 X の密度の増加にともない、 蒸気圧は単調に増加します。 また臨界圧力も単調に増加し、\((T, P)\) 面での臨界線 CL(図中の赤線)は純ファンデルワールス流体の臨界点から、 圧力軸に沿ってまっすぐ伸びる直線になります。