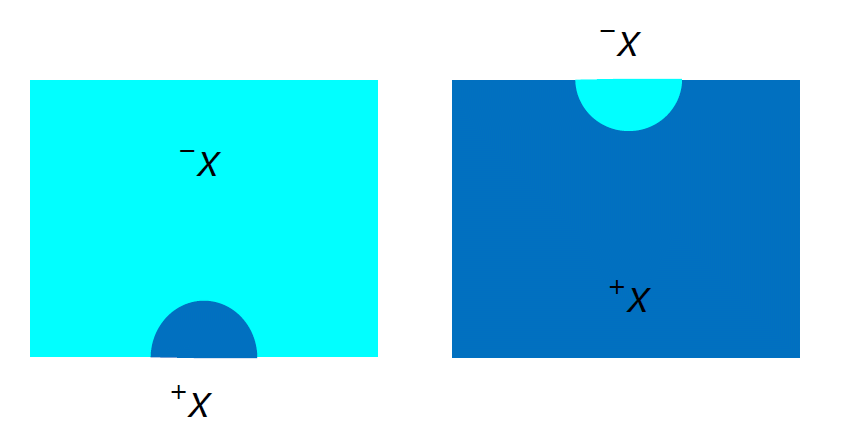
高校までに気液平衡に関わってラウールの法則について学びます。 けれどもそれが2成分系の気液平衡についての法則であることが十分理解されないまま、 しばしば乱暴に理想混合物さらには希薄溶液の話と接合されているようです。 また大学に入って気体と液体が”流体”として統一的に扱われること (臨界温度、圧力以上で気液の区別がなくなること)を学ぶのですが、 それと2成分系の気液平衡がどう関わるかは触れられることがないようです。 ここではまず2成分系についての気液平衡の特徴を簡単に見た後、 気液を統一的に理解しようとする立場から、 2成分系の気液平衡のプロトタイプのありようを眺めてみようと思います。
「溶液」という言葉は、溶媒に溶質が溶け込んだものを意味し、 成分間に明確な主従関係(?)が想定されています。 ここのおはなしでは、各成分を対等に扱うので、 「溶液」ではなく「(液体)混合物」「混合液体」、 「理想溶液」ではなく「理想(液体)混合物」と呼ぶようにします。 このあたりをあげつらうと長くなるのですが、 今日、「理想溶液」は専門的にはもっぱら理想(液体)混合物 ideal (liquid) mixture と呼ぶ方向です。
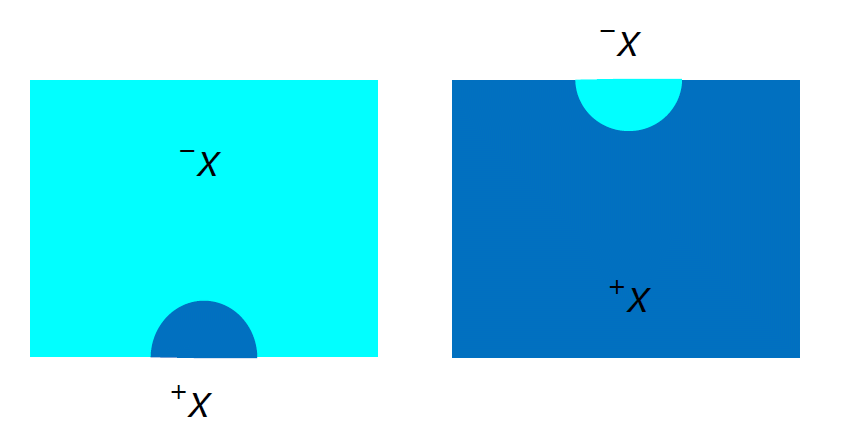
|
| 図 0-1. 2成分系での露点と泡点(沸点)。 同じ温度、組成で比較すると、 蒸気の凝縮圧と液体の蒸気圧はちがいます。 |
蒸気の温度を下げていく、あるいは圧力を上げていくと、ある温度・圧力で液滴が生じ露が浮きます。 この露、液体が生じる点を露点 dew point と呼び、この時の圧力を凝縮圧 condensation (condensing) pressure と呼びます。 一方液体の温度を上げていく、あるいは圧力を下げていくと、ある温度・圧力で気泡が発生し、泡が生じます。 この泡、蒸気が生じる点を泡点 bubble point(沸点)と呼び、この時の圧力を蒸気圧 vapor pressure と呼びます。 純成分、1成分系では露点と泡点は一致し、25 °C で水の凝縮・沸騰は 2.3 kPa(0.02 気圧)で起きます。 けれども2成分系では、気液の成分組成が異なり、 露点と泡点は一般に異なります。
通常は蒸気が発生することを沸騰 boiling と呼び、泡点は沸点 boiling point と呼ばれますが、 特に多成分系の気液平衡を議論する際には、露点 dew point との対比もあって泡点 bubble point と呼ばれます。 このおはなしでも「泡点」あるいは「泡点(沸点)」と呼ぶことにします。
温度一定で圧力を変化させることを考え、 先ほどの凝縮圧(露点)と蒸気圧(泡点)の関係をあからさまに表すと次のようになります:
\begin{equation} {}^- P(x) \le {}^+ P(x) \label{eq:dpbp0} \end{equation}
ここで \(P\) は圧力、\(x\) は混合物の組成(モル分率で表すものとします)で、 左肩に付けた記号は、- が蒸気相(低密度相)、 + が液相(高密度相)を表すものとします。 つまり式 \eqref{eq:dpbp0} はモル分率 \(x\) の混合物の凝縮圧(\({}^- P(x)\))は蒸気圧(\({}^+ P(x)\)) より低いということです。 また気液共存状態では次式が成り立ちます:
\begin{equation} {}^\pm P = {}^+ P({}^+x) = {}^- P({}^- x) \label{eq:dpbp1} \end{equation}
2相共存状態で、蒸気相側の組成 \({}^- x\) の凝縮圧(\({}^- P({}^- x)\))は、 液相側の組成 \({}^+ x\) の蒸気圧(\({}^+ P({}^+ x)\)) に等しいというわけです。 ここで ± は気液共存状態であることを表すものとします (このおはなしでは、 ± 記号を複合同順で使ってみたり、かなり便利使いしますがご容赦ください)。
なお圧力一定で温度を変化させることを考えると、 露点と泡点の関係は次のように書けることになります:
\begin{equation} {}^- T(x) \ge {}^+ T(x) \label{eq:dpbp2} \end{equation}
\begin{equation} {}^+ T({}^+x) = {}^- T({}^- x) \label{eq:dpbp3} \end{equation}
2成分混合系に関わってラウール Raoult の法則はよくご存じでしょう。 ラウールの法則は、ある温度で液体混合物と平衡に存在する蒸気中の分圧と 純成分の蒸気圧の比はモル分率に等しくなることを主張します。 ラウールの法則に従う液体混合物は、 しばしば理想混合物(理想溶液)とされます。
あまりあからさまに問題にされることがないようですが、 ラウールの法則でもっぱら注目するのは泡点(沸点)の方で、 A、B 2成分からなる混合液体について、 ある温度の蒸気圧 \({}^+ P\) に次の関係が成立すると考えます:
\begin{equation} {}^+ P = {}^+ x {}^\pm P^\bullet_\mrm{A} + (1 - {}^+ x) {}^\pm P^\bullet_\mrm{B} \label{eq:rault1a} \end{equation}
ここで \(x\) は A のモル分率、記号の右肩に \(\bullet\) を付けているのは、 混合物ではなく純粋物質についてのものであることを示し、 \({}^\pm P_\mrm{A}^\bullet\) は純粋な A の蒸気圧(= 凝縮圧)に対応します。 これは液体の組成と圧力についての関係式ですが、 蒸気の組成と圧力については次の関係が成立します (蒸気は理想気体として振舞うものとします。 \({}^- x = {}^+ x {}^\pm P^\bullet_\mrm{A}/{}^\pm P\) といった関係に注意します):
\begin{equation} \frac{1}{{}^- P} = \frac{{}^- x}{{}^\pm P^\bullet_\mrm{A}} + \frac{1 - {}^- x}{{}^\pm P^\bullet_\mrm{B}} \label{eq:rault1b} \end{equation}
蒸気の組成から見ると、凝縮圧は重みを付けた純物質の凝縮圧(= 蒸気圧)の調和平均になっています。 算術平均は調和平均より大きく、 これは同じ組成で考えると泡点(沸点)の圧力は、露点の圧力より高いということ(式 \eqref{eq:dpbp0})に対応しています。 また蒸気と液体が平衡に存在する状態を考えると、 気液両相の圧力が等しいので、 平衡圧力 \({}^\pm P\) における気液両相の組成はそれぞれ次式で表されます:
|
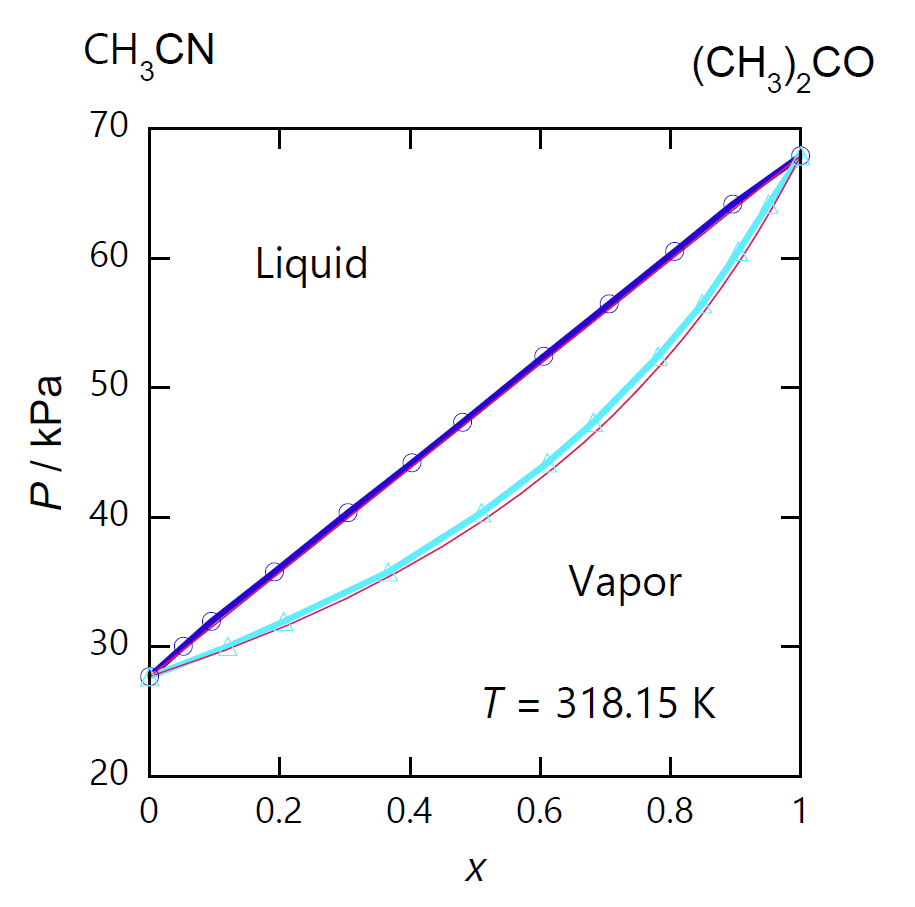
| 図 0-2. アセトン (CH3)2CO とアセトニトリル CH3CN 混合物の 45.0 °C における 泡点曲線と露点曲線(DDB data set #558)。 横軸はアセトンのモル分率。 泡点曲線は青で、露点曲線は水色で示しています。 赤い細い実線はラウールの法則から得られる泡点曲線、露点曲線で、ほぼ実験値と一致しています。 |
\begin{equation} {}^+ x = \frac{{}^\pm P {} - ^\pm P^\bullet_\mrm{B}}{{}^\pm P^\bullet_\mrm{A} - {}^\pm P^\bullet_\mrm{B}} \label{eq:rault2a} \end{equation}
\begin{equation} {}^- x = \frac{({}^\pm P)^{-1} {} - (^\pm P^\bullet_\mrm{B})^{-1}}{({}^\pm P^\bullet_\mrm{A})^{-1} - ({}^\pm P^\bullet_\mrm{B})^{-1}} \label{eq:rault2b} \end{equation}
液体と蒸気を統一的に捉える観点からは、 ラウールの法則は式 \eqref{eq:rault1a} と \eqref{eq:rault1b} あるいは 式 \eqref{eq:rault2a} と \eqref{eq:rault2b} のセットとして取り扱うことになります。
この気液2相の露点と泡点(沸点)の関係を、実際の系について見てみましょう。 図 0-2 にはアセトン (CH3)2CO とアセトニトリル CH3CN 混合系の、 45 °C での露点、泡点と混合物の組成(アセトンのモル分率 x)との関係を示しました。 露点曲線と泡点曲線は純物質(x = 0 と 1)では一致しますが、 混合物では露点より泡点の圧力の方が高くなります(式 \eqref{eq:dpbp0})。 たとえばアセトンとアセトニトリルの物質量比が 1:1(モル分率 0.5)の混合物であれば、 45 °C で、露点は 40 kPa(凝縮圧)ですが、泡点は 48 kPa(蒸気圧)です。 この時、露点(40 kPa)の蒸気中のアセトンのモル分率は 0.50 ですが、 凝縮した露、液体の組成、モル分率は 0.30 です。 また泡点(48 kPa)では液体のモル分率 0.50 に対し気泡中のモル分率は 0.70と、 蒸気と液体で組成が異なります。
ラウールの法則は単純な関係式で気液の相挙動の特徴を捉え、 気液平衡の一つのプロトタイプ(”理想混合物”)を与えるものになっています。 そしてこのプロトタイプを手がかりに、もっと複雑な相挙動を示す種々の系(共沸混合物や液液分離を示す混合物など) の理解が進められていくことになります。
余談ですが、今日「理想混合物(理想溶液)」は、 気液共存状態ではなく、もっぱら等温等圧条件での液体混合物について語られる言葉になっています (成分 \(i\) の化学ポテンシャル \(\mu_i\) について \(\mu_i (T,P,x) = \mu_i^\star(T, P) + RT \ln x_i\))。 また混合物の密度やエンタルピーなどの物性の組成依存性は、気液共存状態ではなく、 もっぱら等温等圧条件で議論されます。 このため等温条件でラウールの法則に従う混合物と 「理想混合物(理想溶液)」の液体の物性を比較するには、 系の蒸気圧と標準圧力(1 bar あるいは 1 atm)の圧力差に応じた偏倚を考慮する必要があります (ポインティング Poynting 補正。 ちなみにポインティングは人名で、 電磁気で登場するポインティングベクトルにも顔を出します)。 通常の条件ではこの偏倚は小さく、 しばしばラウールの法則に従う混合物と「理想混合物(理想溶液)」は同じものと見なされますが、 両者の差異には注意が必要です。
|
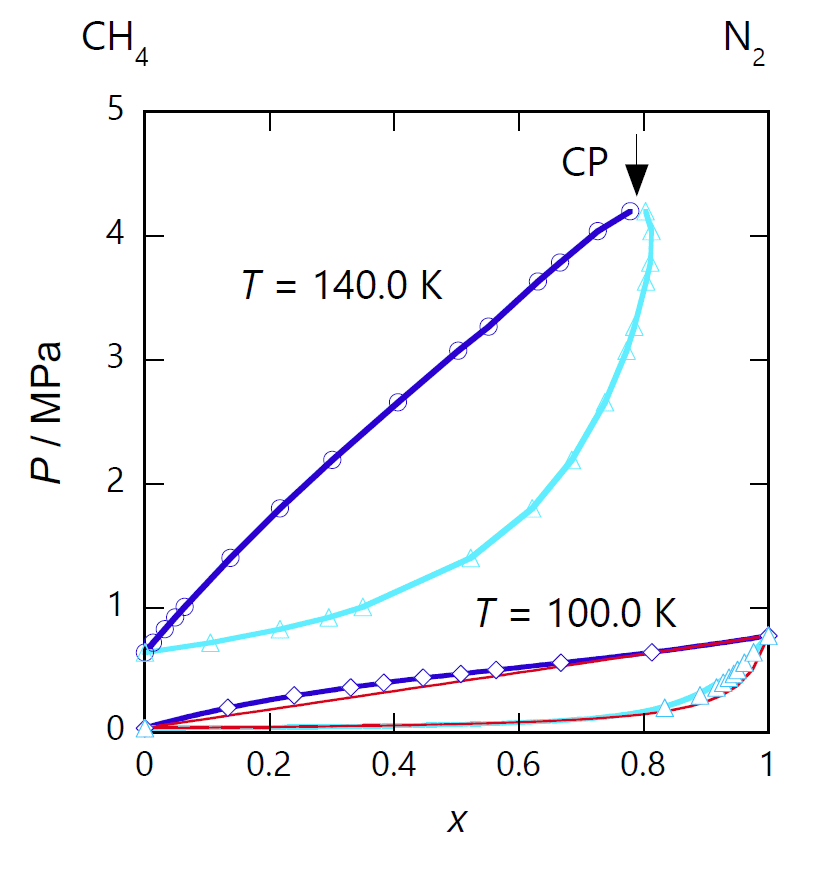
| 図 0-3. 窒素 N2 とメタン CH4 混合物の、 窒素の臨界温度(126.2 K)以上 140 K(DDB data set #415)と、 臨界温度以下 100 K (DDB data set #407)における泡点曲線と露点曲線。 泡点曲線は青で、露点曲線は水色で示しています。 赤い実線はラウールの法則から得られる泡点曲線、露点曲線で、 140 K については窒素の蒸気圧が存在しないので描くことができません。 |
ラウールの法則は現実の液体混合物の気液の相挙動を捉える、 すぐれたプロトタイプ(”理想混合物”)を与えます。 しかしラウールの法則は、 同じ温度で気液の相分離が起きていることを前提としています。 つまり「液体」はどこまでも「液体」であり、 「気体」はどこまでも「気体」なわけです。 けれども臨界温度・圧力以上では液体と気体の区別は無意味であり、 気体と液体は「流体」として同じように振舞います。
図 0-3 に示すのは、窒素 N2(臨界温度 126.2 K、臨界圧力 3.40 MPa) とメタン CH4(臨界温度 190.6 K、臨界圧力 4.6 MPa)混合物の、 等温条件での露点曲線、泡点曲線です。 純物質の臨界温度以下では、 露点、泡点の挙動はラウールの法則から予想されるものを基準(「理想」)に取って、 その差を「非理想性」として扱うこともできるでしょう。
けれども窒素の臨界温度以上、140 K での露点曲線と泡点曲線は、 圧力 4.2 MPa で窒素のモル分率 0.79 で接合して人だま型(?)のループを形成するようになります。 露点曲線と泡点曲線が接合する点では、 露点と泡点の区別がつかなくなります。 圧力の変化で出現する微小な領域(露か泡)が、 元の流体の密度、組成と区別がつかないような状態になる、 つまり臨界点になっています。
そもそも 140 K では純窒素の蒸気圧が存在しませんから、ラウールの法則の適用は不可能です。 このような相挙動に対し、何らかのプロトタイプとなるものは構成できるでしょうか? 気液の一体性、連続性を考慮し気液の相転移を表すプロトタイプとして、 ファンデルワールス状態方程式に従うファンデルワールス流体があります。 1成分の場合には気液の平衡を記述するのに大きな成功を収めたわけですから、 それを2成分に拡張すれば、2成分系の気液の相挙動のプロトタイプが構成できるでしょう。
すでに 19 世紀、ファンデルワールス自身の手で、 2 成分系への拡張が行われました。 ファンデルワールス状態方程式
\begin{equation} P = \frac{n RT}{V - b n} - \frac{a n^2}{V^2} \label{eq:vdw_eq} \end{equation}
において、物質を特徴づけるパラメーター \(a\) と \(b\) を次のように、 組成についての2次の同次式で表すことで、 2成分系に拡張すること自身は容易です(\(a_\mrm{AA}\)、\(a_\mrm{AB}\) 等は、成分 A、B を特徴づけるパラメータ):
\begin{eqnarray} a &=& a_\mrm{AA} x^2 + 2a_\mrm{AB} x (1-x) + a_\mrm{BB} (1-x)^2 \nonumber \\ b &=& b_\mrm{AA} x^2 + 2b_\mrm{AB} x (1-x) + b_\mrm{BB} (1-x)^2 \label{eq:vdw_eq_mix1} \end{eqnarray}
一見単純にも見える外見に関わらず、式 \eqref{eq:vdw_eq}、\eqref{eq:vdw_eq_mix1} から導かれる流体混合物の相挙動は気液平衡に止まらず、 液液平衡は元より、気気平衡、気液液の三相平衡なども包含する非常に多彩なもので、 その全体像が明らかになるのは、 コンピューターの使用が普及する 1960 年代以降のことになります。 そしてそこから導かれた相挙動を手がかりに、 今日では2成分流体の相平衡は、 およそ 6 種類のプロトタイプに分類されるようになりました。
このおはなしでは、そうしたアプローチをもっともっと単純化し、 気液平衡しか現れないケース、 あくまで気体であり続ける流体(理想気体)とファンデルワールス流体の混合系を取り上げ、 2成分系の流体の相挙動の世界の一端を紹介します。