|
|
| 図 3-1. ファンデルワールス流体の飽和密度における並進運動の圧力 \({}^{\pm} \rho^{\star}(T) T\) の温度変化。 蒸気密度 \({}^{-} \rho^{\star}\) については水色で、液相密度 \({}^{+} \rho^{\star}\) については青で示しています。 液相の並進運動の圧力 \({}^{+} \rho^{\star}(T) T\) は温度 \(T\) = 0.2390... で極大となります。 |
前章でみた理想気液混合物の露点・泡点の挙動は理想気体成分 X が、 ファンデルワールス流体 A の気液分離について傍観者として振舞うというだけで、 取り立てて難しいものではありません。 けれども流体の組成、理想気体成分 X のモル分率 \(x\) の観点から整理していくと、 また興味深い相図の世界が広がってきます。
まず気液２相の平衡圧力 \({}^{\pm} P\) の、理想気体成分のモル分率 \(x\) による表現を見てみましょう。 先の関係式から次式が得られます：
\begin{equation} {}^{\pm} P(T, x) = {}^{\pm}P^{\star}(T) + \frac{x}{1 - x} {}^{\pm} \rho^{\star}(T) T \label{eq:mix_tp1} \end{equation}
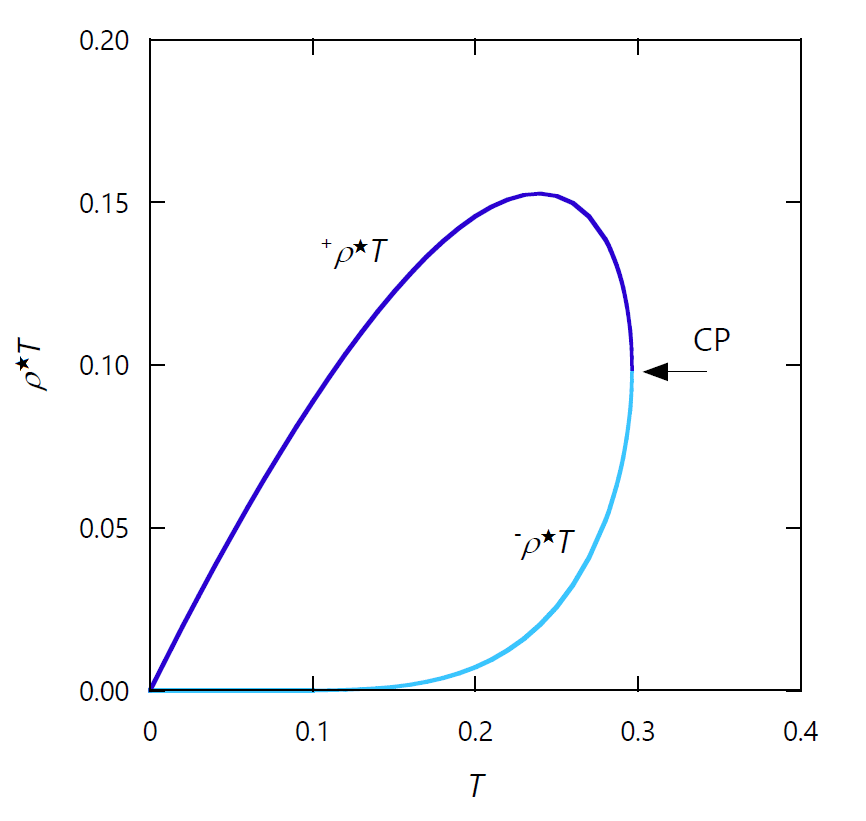
ここで重要になるのは、純ファンデルワールス流体の気液平衡状態の密度に温度をかけたもの \({}^{\pm} \rho^{\star}(T) T\) の挙動です。 \({}^{\pm} \rho^{\star}(T) T\) は、 ビリアル定理からいえば、 飽和密度におけるファンデルワールス流体の圧力に対する分子の並進運動の寄与と言え、 以下では「並進運動の圧力」と呼ぶことにします。 図 3-1 に横軸に温度を取った形で、並進運動の圧力 \({}^{\pm} \rho^{\star}(T) T\) の温度依存性を示しました。 図 3-1 は、図 2-1 の飽和密度曲線を横向きにして、 温度の分だけ縦方向にスケールをかけたものになっていて、 人だま型（吹き出し型？）のループになります。 特に注意したいのは、 飽和液相密度に由来する並進運動の圧力 \({}^{+} \rho^{\star}(T) T\) が温度に対して温度 \(T\) = 0.2390... で極大値 0.1527... を持つことです。 このことが組成比を一定にして 理想気体-ファンデルワールス流体混合物を見た時の、 少し奇妙な振舞いの原因となります。
|
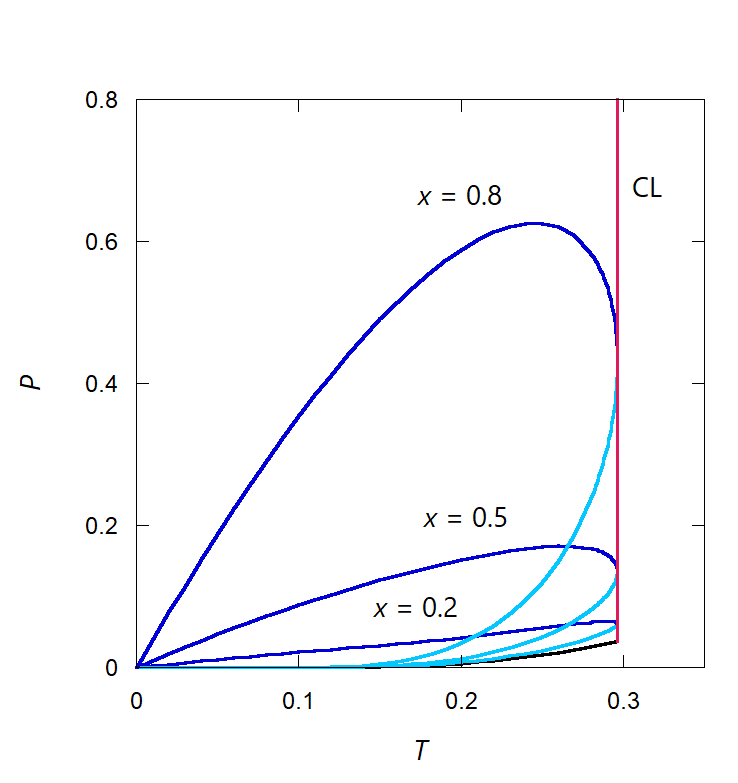
| 図 3-2. 理想気体 X -ファンデルワールス流体 A 混合物の圧力 \(P\) - 温度 \(T\) 面での、 理想気体成分のモル分率 \(x\) を一定に取った等組成線。 露点曲線は水色で、泡点曲線は青で示しています。 図中、赤線は臨界線 critical line です。 |
さて図 3-1 からも分かるように、式 \eqref{eq:mix_tp1} は、 組成（モル分率）が同じ混合流体の露点の圧力（凝縮圧） \({}^{-} P(T, x)\) と泡点（沸点）の圧力（蒸気圧） \({}^{+} P(T, x)\) が異なることを意味します。 たとえば \(T = 0.2\) の場合について見てみると、 純ファンデルワールス流体の蒸気圧（= 凝縮圧）\({}^{\pm}P^{\star}\) は 0.00615 で、 蒸気密度 \({}^{-} \rho^{\star}\) は 0.036、液相密度 \({}^{+} \rho^{\star}\) は 0.729 です。 \(x = 0.8\) とすると露点の圧力は 0.0348（= 0.00615 + (0.8/0.2) × 0.036 × 0.2）、 泡点の圧力は 0.589（= 0.00615 + (0.8/0.2) × 0.729 × 0.2） になります。 こうした事情を、理想気体成分 X のモル分率 \(x\) を一定にして \((P,T)\) 面に描いたのが図 3-2 です。
理想気体成分の密度 \(\rho_\mrm{X}\) を一定に保った時、 理想気体-ファンデルワールス流体混合物の 露点と泡点（沸点）は一致し \((P, T)\) 面での相線は 1 本の曲線 \({}^{\pm}P(T)\) でした（図 2-3）。 けれども組成（モル分率）を一定にして描いた相線では、露点曲線と泡点曲線は一致しません。 温度の上昇とともに泡点曲線は圧力の極大に達した後減少し、 臨界点で露点曲線と接合し、人だま型のループを作ります。 理想気体成分 X のモル分率 \(x\) のループの内部の温度・圧力条件では、 モル分率 \(x\) の混合流体は１相で安定に存在することはできず、 気液の相分離が起きます。
人だまループは理想気体成分のモル分率 \(x\) が増すにつれ、 圧力軸方向に大きく引き伸ばされていきます。 ループの極大となる温度は \(x\) とともに少し低温側に移動しますが、 最終、図 3-1 の並進運動の圧力のループの極大となる温度 0.239... になります。 また臨界温度は組成によらず一定ですから、 臨界線 CL は、純ファンデルワールス流体の臨界点から、 圧力軸に沿ってまっすぐ伸び、 等組成線のループに接します。
ここで注意したいのは、臨界温度、臨界圧力以上で 気液の相分離が起きないかのように扱われることがありますが、 混合流体の場合、一般には成り立ちません。 理想気体-ファンデルワールス流体混合物の場合、 モル分率一定の条件で温度・圧力を変化させた時、 臨界温度以上では相分離は起きませんが、 臨界圧力以上でも相分離が起きます。
このため臨界圧力以上の圧力で温度を上げていったとき、 泡点曲線を２度過る場合が生じます。 たとえば図 3-2 で理想気体成分 X のモル分率 \(x\) が 0.8 の場合（臨界圧力 0.432...）、 圧力 \(P\) が 0.5 だと \(T\) = 0.1537... と 0.2938... で泡点を過ります。 これは液相の温度を上げていったとき \(T\) = 0.154 で蒸気が発生して２相共存状態になった後、 \(T\) = 0.294 で発生した蒸気が凝縮して失われ、再び液相になることを意味します。 こうした温度を上げて凝縮が起きる（あるいは温度を下げて蒸発が起きる）といった現象は、 逆行凝縮・蒸発として知られる、２成分混合系で一般に見られる現象です。