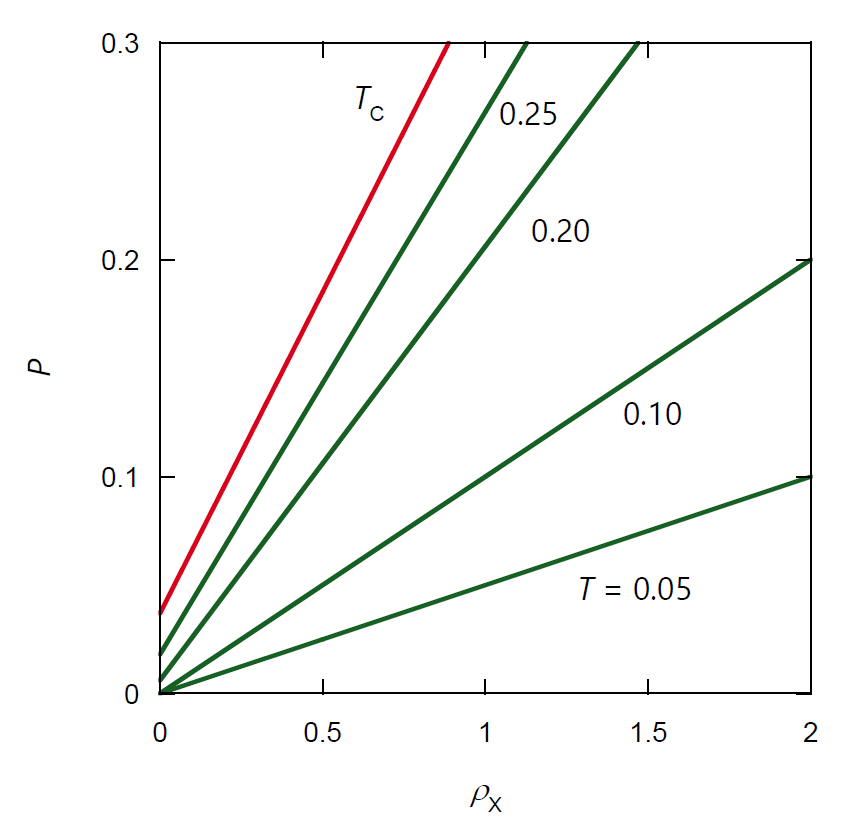
|
|
| 図 4-1. 種々の温度における、 理想気体 X -ファンデルワールス流体 A 混合物の蒸気圧（= 凝縮圧）\({}^\pm P\) の理想気体成分 X の密度 \(\rho_\mrm{X}\) 依存性 （式 \eqref{eq:mix_coex1}）。 図中、赤線は臨界温度 \(T_\mrm{C}\)（= 8/27）におけるもので臨界線に相当。 |
２成分流体系の相挙動の実験的な研究は、 たいていの場合、平衡時の温度・圧力と各相の成分の組成比に注目して行われます。 理想気体 - ファンデルワールス流体混合物の場合、 温度 \(T\)・圧力 \(P\) と理想気体成分の密度 \(\rho_\mrm{X}\) に注目した相挙動は、先の図 2-3 に見たように単純ですが、 組成比（モル分率）に注目すると \((P, T) \)面での等組成線が露点と泡点で一致しなかったように、 いささか輻輳した挙動が現れます。 ここからは端的に、理想気体成分 X のモル分率 \(x\) を横軸に取った相図を見てみます。
この章では露点・泡点の圧力（凝縮圧・蒸気圧）を取り上げます。 すでに見たように、 理想気体 - ファンデルワールス流体混合物の凝縮圧 \({}^- P\) と蒸気圧 \({}^+ P\) は、 理想気体成分 X の密度 \(\rho_\mrm{X}\) が同じであれば一致します：
\begin{equation} {}^{\pm} P(T, \rho_\mrm{X}) = {}^{\pm}P^{\star}(T) + \rho_\mrm{X} T \label{eq:mix_coex1} \end{equation}
図 4-1 には式 \eqref{eq:mix_coex1} の関係を \((P, \rho_\mrm{X}) \) 面であからさまに示してみました。 温度が一定であれば凝縮圧・蒸気圧は理想気体成分の密度 \(\rho_\mrm{X}\) に対し直線的に増加します。 その勾配は温度に等しく、 切片（純ファンデルワールス流体 A の蒸気圧）は温度とともに指数関数的に増加します。
この図 4-1 の \((P, \rho_\mrm{X}) \) 面での露点・泡点の１本の等温線は、 横軸に理想気体成分 X のモル分率 \(x\) をとり \((P, x) \) 面で表すと、 純ファンデルワールス流体（\(x\) = 0）での蒸気圧（= 凝縮圧）から始まる、 露点と泡点２本の曲線に分裂することになります：
\begin{equation} {}^{\pm} P(T, x) = {}^{\pm}P^{\star}(T) + \frac{x}{1 - x} {}^{\pm} \rho^{\star}(T) T \label{eq:mix_tp1} \end{equation}
|
|
| 図 4-2a. 理想気体 X -ファンデルワールス流体 A 混合物の \((P, x) \)面の相線。 露点曲線は水色で、泡点（沸点）曲線は青で示しています。 等温線が少し入り組むので、マーカーを付してみました。 \(T\) = 0.1 での露点曲線は逆 L 字型で、ほとんど座標軸に張り付いています。 図中、赤線は臨界温度での等温線です。 臨界温度 \(T_\mrm{C}\)（= 8/27 = 0.296...）以上では蒸発・凝縮現象は生じません。 | 図 4-2b. 理想気体 X -ファンデルワールス流体 A 混合物の \((P, x) \)面の相線の臨界温度付近の拡大図。 露点曲線は水色で、泡点（沸点）曲線は青で示しています。 温度を上げるに従い、露点曲線は単調に臨界線に収束していきますが、 泡点曲線は少し複雑な挙動を示します。 図中、赤線は臨界温度での等温線です。 |
図 4-2 に示すのは、 \((P, x)\) 面の等温条件での相線です。 式 \eqref{eq:mix_tp1} に見るように、 凝縮圧（露点）・蒸気圧（泡点）の等温線は理想気体成分 X のモル分率に対し直角双曲線 \(x/(1-x)\) に従い、 露点曲線・泡点曲線は \(x\) の増加にともない単調に増加し \(x = 1\) で発散します。 露点曲線・泡点曲線の増加量は、それぞれファンデルワールス流体の飽和蒸気、飽和液体の並進運動の圧力 \({}^{\pm} \rho^{\star}(T) T\) に比例します。
図 3-1 で見たように露点におけるファンデルワールス流体の並進運動の圧力 \({}^- \rho^\star T\) は、 温度に対して単調に増加するので、凝縮圧（露点圧力）は温度とともに単調に増加し、 臨界線に収束していきます。 また低温では飽和蒸気密度はきわめて小さく、 露点曲線は逆 L 字(⌋)型になります。 たとえば \(T\) = 0.1 で A の飽和液密度 \({}^{+} \rho^{\star}\) は 0.887ですが、 飽和蒸気密度 \({}^{-} \rho^{\star}\) は 0.000409... です。 ですから図 1-8a 中の \(T\) = 0.1 の泡点曲線がファンデルワールス流体の臨界圧力 \(P^\star_\mrm{C} \)（0.037...）に達するのは、\(x\) = 0.294 ですが、 露点曲線では、\(x\) = 0.999 となります。
凝縮圧（露点圧力）に比して、蒸気圧（泡点圧力）の等温線の挙動は少し入り組んでいます。 図 4-2b には凝縮圧・蒸気圧の等温線の臨界温度付近の拡大図を示しました。 泡点におけるファンデルワールス流体の並進運動の圧力 \({}^+ \rho^\star T\) は温度 \(T\) = 0.2390... で極大を示します （図 3-1）。 このため泡点曲線（蒸気圧の等温線）は \(x\) = 0 付近では温度とともに増加する一方、 \(T\) = 0.2390... 以上では \(x\) の大きいところで減少します。 そして最終、臨界温度で露点曲線と接合して臨界線となります（式 \eqref{eq:mix_tp1}）。
気体の溶解度という観点から見ると、 泡点の挙動はヘンリーの法則に対応しています。 理想気体成分 X の液相中のモル分率 \({}^- x\) は、 X の密度が小さければ（\(\rho_\mrm{X} \ll {}^+\rho^\star\)）、次式のように蒸気相中の X の分圧 \(P_\mrm{X} = \rho_\mrm{X} T\) を用い次式のように表せます：
\begin{equation} {}^+ x = \frac{\rho_\mrm{X}}{\rho_\mrm{X} + {}^+\rho_\mrm{A}} \approx \frac{\rho_\mrm{X}}{{}^+ \rho^\star(T)} = \frac{1}{{}^+ \rho^\star(T) T} P_\mrm{X} \label{eq:henry} \end{equation}
つまり理想気体成分 X のファンデルワールス流体中のモル分率（溶解度といってもよい）は、 蒸気相中の X の分圧に比例し、 その比例定数（ヘンリー定数）\(k_\mrm{H}\) は \(1/({}^+ \rho^\star(T) T) \) になるということです。 ちなみにオストワルドの溶解係数は、 1 です。