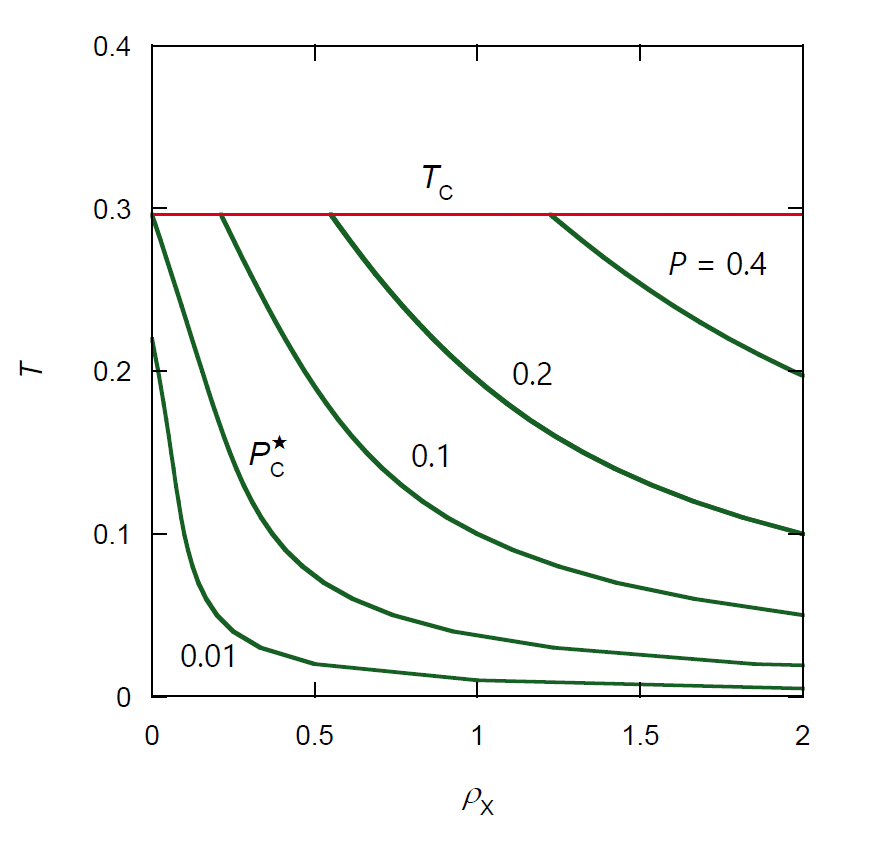
|
|
| 図 5-1. 種々の圧力における、 理想気体 X -ファンデルワールス流体 A 混合物の露点・泡点温度 \({}^\pm T\) の理想気体成分 X の密度 \(\rho_\mrm{X}\) 依存性 （式 \eqref{eq:dxpteq}）。 |
前章では温度一定での、露点・泡点の圧力の流体組成依存性に注目しました。 ここでは圧力一定での露点・泡点の温度と理想気体成分との関係を見てみましょう。
理想気液混合物（理想気体-ファンデルワールス流体混合物）の露点・泡点の圧力の関係式を、 理想気体成分 X の密度 \(\rho_\mrm{X}\) についての関係式として書くと次式になります：
\begin{equation} \rho_\mrm{X} = \frac{P - {}^{\pm} P^\star (T)}{T} = \frac{\Delta P(T)}{T} \label{eq:dxpteq} \end{equation}
ここで \(\Delta P(T) = P - {}^{\pm} P^\star (T)\) とおきました。 式 \eqref{eq:dxpteq} は、温度 \(T\)、圧力 \(P\) での気液平衡状態における、 気液両相の理想気体成分 X の密度 \(\rho_\mrm{X}\)（\(= {}^{\pm} \rho_\mrm{X}\)）を与える式になっています。 圧力が純ファンデルワールス流体の蒸気圧より小さければ（\(\Delta P(T) \lt 0\)）、 気液の相分離は起きません。 また理想気体成分 X の臨界密度 \(\rho_\mrm{C, X}\) は次式で与えられます：
\begin{equation} \rho_\mrm{C, X} = \frac{P - P_\mrm{C}^\star}{T_\mrm{C}} = \frac{27}{8} P - \frac{1}{8} \label{eq:critdx} \end{equation}
図 5-1 には露点と泡点の温度の理想気体成分 X の密度 \(\rho_\mrm{X}\) 依存性を示しました（露点と泡点の温度は一致します）。 圧力が純ファンデルワールス流体の臨界圧力 \(P_\mrm{C}^\star\) より小さい時には、 等圧線の温度は \(\rho_\mrm{X}\) = 0 で純ファンデルワールス流体の露点・泡点（\({}^{\pm} T^\star\)） から始まって \(\rho_\mrm{X}\) の増加とともに減少していきます。 一方圧力が純ファンデルワールス流体の臨界圧力より大きい時には、 式 \eqref{eq:critdx} で与えられる臨界密度 \(\rho_\mrm{C, X}\) で、臨界温度（\(T_\mrm{C}\)） から始まって減少し、 十分温度が低くなると（\(P \gg {}^{\pm} P^\star (T)\)）、 ほぼ \(\rho_\mrm{X}\) に反比例して減少します（\({}^\pm T \approx P/\rho_\mrm{X}\)）。
前章の図 4-2 に見るように、 相図の \((P, x)\) 面での等温線は組成に対し単調な挙動（直角双曲線）を示しますが、 \((T, x)\) 面での等圧線は少し入り組んでいます。 式 \eqref{eq:dxpteq} を平衡組成 \({}^{\pm} x(T, P)\) について書き直すと次式のようになります：
\begin{equation} {}^{\pm} x(T, P) = \frac{\rho_\mrm{X}}{\rho_\mrm{X} + {}^\pm \rho^\star(T)} = \frac{\Delta P(T)}{\Delta P(T) + {}^{\pm} \rho^\star (T) T} \left ( = \frac{P - {}^{\pm} P^\star (T)}{P - {}^{\pm}P^\star (T) + {}^{\pm} \rho^\star (T) T} \right ) \label{eq:mix_mf1} \end{equation}
圧力 \(P\) が純粋なファンデルワールス流体の臨界圧力 \(P^\star_\mrm{C}\) より低ければ、 \(x = 0\) で露点と泡点は一致します。 そして理想気体成分 X のモル分率 \(x\) の増加とともに、露点・泡点ともに低下しますが、 モル分率 \(x\) が小さい間は泡点の低下の方が著しく両者の差は拡大しますが、 泡点の低下が落ち着く一方、露点が \(x = 1\) 付近で急速に低下し、両者は \(x = 1\) で \(T = 0\) に収束します。
圧力 \(P\) が純粋なファンデルワールス流体の臨界圧力よりも高い場合は、 常に \(\Delta P(T) \gt 0\) で \({}^\pm x \gt 0\) になります。 この場合、露点曲線と泡点曲線は臨界温度で極大となり接合します。 接合の起きる混合流体の組成、理想気体成分の臨界モル分率 \(x_\mrm{C}(T_\mrm{C}, P)\) は、 下式で与えられます：
\begin{equation} x_\mrm{C}(T_\mrm{C}, P) = \frac{\Delta P(T_\mrm{C})}{\Delta P(T_\mrm{C}) + {}^{\pm} \rho_\mrm{C}^\star T_\mrm{C}} = \frac{P - 1/27}{P + 5/81} \label{eq:mix_mf2} \end{equation}
十分圧力が高い時には、臨界モル分率 \(x_\mrm{C}(T_\mrm{C}, P)\) は次式のようになります：
\begin{equation} x_\mrm{C}(T_\mrm{C}, P) \approx 1 - \frac{8}{81 P} \label{eq:mix_mf2x} \end{equation}
臨界点で露点と沸点は一致しますが、温度を下げるに従い露点と泡点のモル分率 \({}^\pm x\) は異なる挙動を示します。 露点は温度が下がるに従い、 理想気体成分 X のモル分率 \({}^- x\) は、臨界モル分率 \(x_\mrm{C}(T_\mrm{C}, P)\) から \(x = 1\) に単調に増加します。 一方泡点曲線では \({}^+ \rho(T) T\) が温度の変化にともない極大を示すことを反映して、 温度が下がるに従いモル分率 \({}^+ x\) は臨界モル分率 \(x_\mrm{C}(T_\mrm{C}, P)\) から最初減少し、 極小値を経て増加し ”腹” の膨れた形になります。
|
|
| 図 5-2a. 理想気体-ファンデルワールス流体混合物の \((T, x) \)面の露点と泡点（沸点）の等圧線図。 露点曲線は水色で、泡点曲線は青で示しています。 図中、赤線は臨界温度、臨界線です。 臨界温度 \(T_\mrm{C}\)（= 8/27 = 0.296...）以上では蒸発・凝縮現象は生じません。 | 図 5-2b. 理想気体-ファンデルワールス流体混合物の \((T, x) \)面の露点と泡点の等圧線の拡大図。 圧力が下がり、ファンデルワールス流体の臨界圧力 \(P^\star_\mrm{C}\)（= 1/27 = 0.037...）に近づくにつれ等圧線のループの先端は尖り、 臨界圧力ではループを構成する露点曲線、泡点曲線は、 純ファンデルワールス流体の臨界点に、 勾配 16/81 = 0.1975... で接します。 |
図 5-2a には、こうして得られる \((T, x)\) 面の、 臨界圧力以上と臨界圧力以下での、等圧条件での露点曲線と泡点曲線を示しました。 圧力が純ファンデルワールス流体の臨界圧力 \(P^\star_\mrm{C}\) 以上では、露点曲線と泡点曲線は臨界点で接合し、 臨界線と接して、人だま型のループを構成します。 臨界圧力以上ではモル分率一定で温度を変化させると、 臨界モル分率 \(x_\mrm{C}\) 以下の組成で泡点曲線と２度交わることが起きますが、 これは先にも触れた逆行凝縮・沸騰現象をもたらすことになります。 一方、臨界圧力以下では、 理想気体成分の増加とともに、 露点曲線と泡点曲線は純ファンデルワールス流体の露点（泡点）から、 それぞれ異なる勾配で減少していきます。
もう少し具体的に相線の勾配の表現を見ると、 次式のようになります（微分記号 \(\rmd\) は、相線に沿っての微分を意味するものとします）：
\begin{equation} \frac{\rmd {}^{\pm} x}{\rmd T} = -\frac{1}{(\Delta P + {}^{\pm} \rho^\star T)^2} \lpar{\frac{\rmd P^\star}{\rmd T} {}^{\pm} \rho^\star T + \Delta P \frac{\rmd ({}^{\pm} \rho^\star T)}{\rmd T}} \label{eq:mix_mf3} \end{equation}
圧力が純ファンデルワールス流体の臨界圧力 \(P^\star_\mrm{C}\) 以上の場合、 臨界温度 \(T_\mrm{C}\)（= \(T^\star_\mrm{C}\) ）で並進運動の圧力の温度微分 \(\rmd ({}^{\pm} \rho^\star T)/\rmd T\) は発散し （図 3-1）、 露点曲線、泡点曲線の臨界温度での勾配 \(\rmd T/\rmd {}^{\pm} x\) は 0 で、 露点、泡点は極値を取ります。
一般に混合流体系の \((T, x)\) 面の相線で、臨界点は等圧線の極大（あるいは極小）に対応します （液液分離では上部臨界温度（あるいは下部臨界温度）としておなじみでしょう）。
臨界圧力・臨界温度で、純ファンデルワールス流体の蒸気圧曲線の勾配 \(\rmd P/\rmd T\) は 1/2 なので \(x = 0\) における露点曲線、泡点曲線の勾配は次式で与えられます（\(\Delta P = 0\) になっていることに注意）：
\begin{equation} \left. \frac{\rmd T}{\rmd {}^{\pm} x} \right|_{P_\mrm{C}, ~x=0} = \rho_\mrm{C}^\star T_\mrm{C} ~ \left. \frac{\rmd ~T}{\rmd P}\right|_{P_\mrm{C}, ~x=0} = \frac{16}{81} \label{eq:mix_mfx} \end{equation}
図 5-2b には式純ファンデルワールス流体の臨界圧力（\(P^\star_\mrm{C}\) = 1/27 = 0.0370...）付近の相線と \eqref{eq:mix_mfx} に対応する勾配を描きました。 圧力を下げるとともに露点曲線と泡点曲線が作る人だま型の滑らかなループが、 純ファンデルワールス流体の臨界圧力 \(P^\star_\mrm{C}\) を境に、 先端が嘴（くちばし）型の尖ったループになり、 さらにその嘴が開いていきます。