２成分系になることで 気液２相共存状態がどのような振る舞いをするか見てきたわけですが、 そもそもの相の安定性自体に注目してみましょう。
|
|
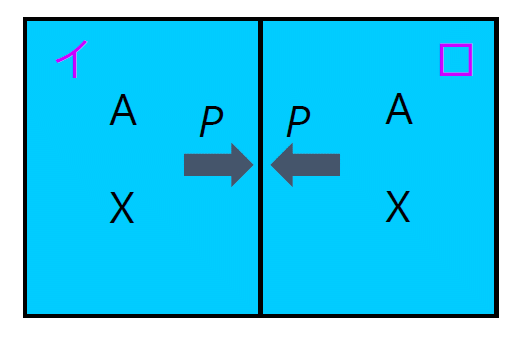
| 図 6-1. 機械的不安定性のイメージ。 流体がイとロ２つの部屋にピストンで隔てられた状況を考え、 圧力の釣り合いが安定化かどうかを問題にします。 |
微視的に眺めてみると、 わずかな密度の増加が圧力の減少をもたらす （あるいは密度の減少が圧力の増加をもたらす）なら、 相を安定に維持することができません。 図 6-2 のように温度一定で、 ある容器の中に閉じ込められたA、X ２成分からなる流体を考え、 これがピストンでイとロ、２つの部屋に隔てられ、 圧力が等しく釣り合っているとします。 この状態で仮にイの圧力が少し増加したとすると力の釣り合いが破れ、 ピストンがロの側に移動し、イの密度は減少、ロの密度は増加します。 密度の増加にともない圧力が増加（\(\partial P/\partial \rho \gt 0\)）するのであれば、 イの圧力は減少、ロの圧力は増加して、すぐに圧力の釣り合いは回復します。 つまり相は安定なわけです。 けれども密度の増加にともない圧力が減少（\(\partial P/\partial \rho \lt 0\)）するような状況であれば、 イの圧力のわずかな増加は、イの密度の減少とさらなるイの圧力の増加、 そしてロの密度の増加とさらなる圧力の減少を招き、 圧力の不均衡は雪だるま式に拡大します。 こうした相の不安定性を機械的不安定性 mechanical instability と呼びます。 ここで考えている圧力の密度依存性は A と X の組成比が一定のままで考えていますから、 機械的不安定性の条件は次式で与えられます：
\begin{equation} \pdifA{P}{\rho}{T, x} = (1-x) \left[ \frac{T}{(1 - \rho_\mrm{A})^2} - 2 \rho_\mrm{A} \right]+ x T \le 0 \label{eq:mech_insta} \end{equation}
|
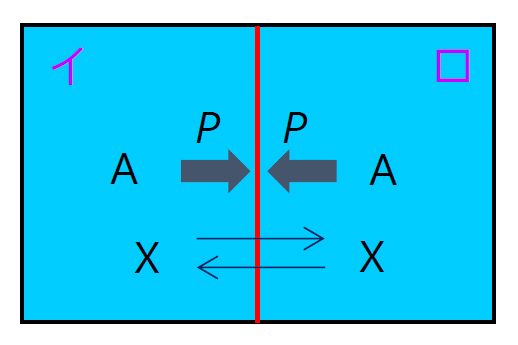
| 図 6-2. 物質不安定性のイメージ。 ピストンの素材が器壁の素材と異なり、 ファンデルワールス流体成分 A はピストンを透過できませんが、 理想気体成分はピストンをすり抜けます。 |
上記の機械的不安定性では、イとロ、２つの部屋を隔てるピストンの素材が、 流体を閉じ込めている器壁同様、 A も X も透過しないと考えていました。 けれども図 6-2 に示すように、 ピストンの素材が、流体を閉じ込めている器壁の素材と異なり、 理想気体成分 X を自由に透過させる素材でできていると考えるとどうでしょうか？ この場合、理想気体成分 X はピストンをすり抜けてしまい、 ピストンが移動しても X の密度が変化しないので、 不安定性の条件は次式で表されます：
\begin{equation} \pdifA{P}{\rho_\mrm{A}}{T, \rho_\mrm{X}} = \pdifA{P^\star}{\rho_\mrm{A}}{T} = \frac{T}{(1 - \rho_\mrm{A})^2} - 2 \rho_\mrm{A} \le 0 \label{eq:mat_insta} \end{equation}
この不安定性は、 流体中に成分組成比の不均一さをもたらし、 物質不安定性 material instability（あるいは拡散不安定性 diffusional instability）と呼ばれます。 式 \eqref{eq:mech_insta}, \eqref{eq:mat_insta} から明らかに、 機械的不安定性（式 \eqref{eq:mech_insta}）が成り立っておれば、必ず物質不安定性（式 \eqref{eq:mat_insta}）が成り立ちます。 あるいは物質不安定性があっても、 機械的不安定性を示すとは限りません。 ですから相の安定性の限界を与えるスピノーダル線は、 物質的不安定性の条件によって決まることになります。
|
| 図 6-3. 気液の共存線と相の安定性の限界。 水色の実線は露点曲線、青は泡点曲線です。 相の安定性の限界（スピノーダル線）は、 蒸気相については水色、液相については青の点線で示しています。 橙色の点線は機械的不安定性から評価される不安定領域（式 \eqref{eq:mech_insta}）の境界で、 理想気体成分の密度を一定に保った場合（\(\rho_\mrm{X} = 0.5\)。薄い橙色）と モル分率一定に保った場合（\(x\) = 0.5。濃い橙色）について描いてあります。 |
ファンデルワールス流体成分 A が成分 X と独立に挙動することに注意するなら、 相の不安定性の条件は純ファンデルワールス流体の場合と同等になるはずです。 実際、物質的不安定性の条件（式 \eqref{eq:mat_insta}）から得られるスピノーダル温度 \(T_\mrm{sn}\) は次式のように、 ファンデルワールス流体成分 A の密度で決まり、 理想気体成分の密度に依存せず、純ファンデルワールス流体と同じになります：
\begin{equation} T_\mrm{sn} = 2 \rho_\mrm{A} (1 - \rho_\mrm{A})^2 = T^\star_\mrm{sn} \label{eq:t_sp} \end{equation}
スピノーダル温度を成分 A の密度 \(\rho_\mrm{A}\) の関数と見た時、 密度 \(\rho_\mrm{A}\) についての微分 \(T'_\mrm{sn}(\rho_\mrm{A})\) は次式のようになります：
\begin{equation} T'_\mrm{sn}(\rho_\mrm{A}) \equiv \frac{\rmd T_\mrm{sn}}{\rmd \rho_\mrm{A}} = 2 (1 - \rho_\mrm{A}) (1 - 3 \rho_\mrm{A}) \label{eq:t_spder} \end{equation}
スピノーダル温度は成分 A の臨界密度 \(\rho_\mrm{C, A}\) = 1/3 で極大となり、 極大温度は気液の臨界温度 \(T_\mrm{C}\) = 8/27 と一致します。
図 6-3 にはスピノーダル温度 \(T_\mrm{sn}\)（図中の点線）を気液の相共存温度（露点・泡点温度）とともに、 ファンデルワールス流体成分 A の密度に対して示しました。 気液の臨界点は気液両相が不安定になる点でもあり、 スピノーダル線は気液の相境界と臨界点で接する形になります。 そしてスピノーダル線は臨界点を境に、 蒸気相のスピノーダル線（\(T_\mrm{sn}(\rho_\mrm{A} \lt 1/3)\)）、 液相のスピノーダル線（\(T_\mrm{sn}(\rho_\mrm{A} \gt 1/3)\)）とに分けて考えることができます。
一方、機械的不安定性の条件（式 \eqref{eq:mech_insta}）から得られる不安定さの境界は、 理想気体成分の密度 \(\rho_\mrm{X}\) あるいはモル分率 \(x\) によって変化しますが、 気液の相境界は無論、スピノーダル線より低温側にあります。 機械的不安定性の領域を、気相、液相の安定性の限界と対応付けることは困難です。 機械的不安定性は混合流体の相挙動を考える上では、 あまり重要でないと言えるでしょう。
理想気体-ファンデルワールス流体混合物に限らず、 混合流体系では一般に機械的不安定性は物質不安定性をもたらしますが、 その逆は成り立ちません。
スピノーダル温度は、気液の露点・泡点温度同様、 理想気体成分の影響を受けず、 純ファンデルワールス流体と同じです（式 \eqref{eq:t_sp}）。 理想気体成分の影響はスピノーダル圧力 \(P_\mrm{sn}\) に現れ、 先に露点・泡点曲線で見たように、 理想気体成分 X の密度に依存して次式のように表されます：
\begin{equation} P_\mrm{sn} = \rho_\mrm{A}^2 (1 - 2\rho_\mrm{A}) + \rho_\mrm{X} T_\mrm{sn} = P^\star_\mrm{sn} + \rho_\mrm{X} T_\mrm{sn} \label{eq:p_sp} \end{equation}
スピノーダル圧力をスピノーダル温度同様に、 成分 A の密度 \(\rho_\mrm{A}\) の関数と見た時、 式 \eqref{eq:p_sp} から密度 \(\rho_\mrm{A}\) についての微分 \(P'_\mrm{sn}(\rho_\mrm{X}; \rho_\mrm{A})\) は次式のようになります：
\begin{equation} P'_\mrm{sn}(\rho_\mrm{A}; \rho_\mrm{X}) = 2 \rho_\mrm{A} (1 - 3\rho_\mrm{A}) + \rho_\mrm{X} T'_\mrm{sn}(\rho_\mrm{A}) \label{eq:p_spdd} \end{equation}
|
| 図 6-4. 理想気体-ファンデルワールス流体混合物の \((P, T)\) 面でのスピノーダル線。 理想気体成分の密度 \(\rho_\mrm{X}\) が 0.5 の場合。 黒い実線は露点・泡点曲線で、 蒸気相のスピノーダルは水色、液相のスピノーダルは青の点線で示しています。 橙色の点線は機械的不安定性から評価される不安定領域です。 純粋なファンデルワールス流体（\(\rho_\mrm{X}\) = 0）の露点・泡点曲線とスピノーダルも表示してあります。 純粋なファンデルワールス流体では、機械的不安定性から評価される不安定領域はスピノーダル線と一致します。 |
ここで \(P'_\mrm{sn}(\rho_\mrm{A}; \rho_\mrm{X})\) は \(\rho_\mrm{X}\) を一定とした \(\rho_\mrm{A}\) についてのスピノーダル圧力の微分です。 物質不安定性の関係式 \eqref{eq:mat_insta} からも明かですが、 臨界密度で \(P'_\mrm{sn}(\rho_\mrm{A}; \rho_\mrm{X})\) は 0 になります。
\begin{equation} P'_\mrm{sn}(\rho_\mrm{C, A}; \rho_\mrm{X}) = \rho_\mrm{X} T'_\mrm{sn}(\rho_\mrm{C, A}) = 0 \label{eq:p_spddcp} \end{equation}
スピノーダル温度の密度微分も臨界密度で 0 になり符号を変えるので（式 \eqref{eq:t_spder}）、 \(\rho_\mrm{X}\) 一定で、 \((P, T)\) 面でのスピノーダル線は臨界点で尖点（カスプ）を持ちます。 また臨界点でのスピノーダル線の勾配は、式 \eqref{eq:t_spder} と 式 \eqref{eq:p_spdd} から、 次式のようになります：
\begin{equation} \left. \frac{\rmd P_\mrm{sn}(\rho_\mrm{A}; \rho_\mrm{X})}{\rmd T_\mrm{sn}(\rho_\mrm{A})} \right |_{\rho_\mrm{A} = \rho_\mrm{C, A}} = \frac{1}{2} + \rho_\mrm{X} \label{eq:cp_slopept} \end{equation}
図 6-4 には理想気体成分 X の密度を一定にとった場合の、 \((P, T)\) 面での典型的なスピノーダル線を示しました。 露点・泡点曲線同様、 スピノーダル線も理想気体成分の存在によって高圧側に押し上げられる形です。 図には機械的不安定性の境界（橙色の点線）も示しました。 機械的不安定性の領域は狭く、図の \(\rho_\mrm{X}\) = 0.5 の場合には、 温度 \(T\) = 0.2037... 以上の温度では相の不安定性が生じず（図 6-3）、 また露点の圧力（凝縮圧）、またそれ以上の圧力でも不安定性が生じないことになります。
理想気体成分 X の密度を一定にとった場合は、 純粋なファンデルワールス流体の場合のスピノーダル線が高圧側に押し上げられるだけでした。 しかし組成比、モル分率に注目すると少し変わった挙動が現れます。 先のスピノーダル圧力の式 \eqref{eq:p_sp} をモル分率 \(x\) と ファンデルワールス流体成分の密度 \(\rho_\mrm{A}\) で書き換えると、露点・泡点の場合同様、次式になります：
\begin{equation} P_\mrm{sn} = P^\star_\mrm{sn} + \frac{x}{1 - x} \rho_\mrm{A} T_\mrm{sn} \label{eq:p_spx} \end{equation}
|
| 図 6-5. 理想気体-ファンデルワールス流体混合物の \((P, T)\) 面でのスピノーダル線。 理想気体成分の密度 \(\rho_\mrm{X}\) が 0.5 の場合。 黒い実線は露点・泡点曲線で、 蒸気相のスピノーダルは水色、液相のスピノーダルは青の点線で示しています。 橙色の点線は機械的不安定性から評価される不安定領域です。 純粋なファンデルワールス流体（\(\rho_\mrm{X}\) = 0）の露点・泡点曲線とスピノーダルも表示してあります。 純粋なファンデルワールス流体では、機械的不安定性から評価される不安定領域はスピノーダル線と一致します。 |
理想気体成分 X の密度 \(\rho_\mrm{X}\) を一定に取った場合（式 \eqref{eq:p_spddcp}）と異なり、 理想気体成分 X のモル分率 \(x\) を一定にとった場合は、 スピノーダル圧力の密度微分は臨界密度で 0 にならず、尖点は生じません：
\begin{equation} P'_\mrm{sn}(\rho_\mrm{C, A}; x) = \frac{x}{1 - x} T_\mrm{sn}(\rho_\mrm{C, A}) = \frac{x}{1 - x} T^\star_\mrm{C} \label{eq:p_spxdevcp} \end{equation}
図 6-5 には、モル分率 \(x\) = 0.5 の場合の \((P, T)\) 面のスピノーダル線を示しました。 気液の相線では、理想気体成分 X のモル分率が増加するにつれ、 露点曲線に比べ、 泡点曲線の圧力が高く押し上げられ、ループを形成するようになりました。 同様のことがスピノーダル線についても起き、 液相のスピノーダル線の圧力が蒸気相のスピノーダル線より高く押し上げられ、 ループが形成されます。 ただし液相のスピノーダル圧力が大きな負の値を取るので、 スピノーダル線はよじれたリボン（？）のような形状になります。 そしてよじれたリボンの内部の \((P, T)\) 領域は、 所定のモル分率では安定に実現できません。
なおモル分率一定でみた機械的不安定性の \((P, T)\) 面の挙動には尖点が現れます。 けれどもスピノーダル領域の内部で、 すでに相の不安定性が起きている状況なので、何らかの相挙動と結びつくものにはならないようです。
図 6-4、図 6-5 に見る、 組成比を一定にした条件での \((P, T)\) 面での相線とスピノーダル線の関係は、 あらわにモル分率を横軸に取った相図においても見られるところです。 図 6-6 には \((P, x)\)面の、図 6-7 には \((T, x)\)面の露点・泡点とスピノーダル線の挙動を示しました。 相線とスピノーダル線は臨界点で一致しますが、 臨界点から延びるスピノーダル線と相線を全体としてみた時も、 スピノーダル線は定性的には相線の挙動をなぞっています。
|
|
| 図 6-6. 理想気体-ファンデルワールス流体混合物の \((P, x)\) 面でのスピノーダルの等温線。 実線は相線で露点曲線は水色で、沸点曲線は青で示しています。 蒸気相のスピノーダルは水色、液相のスピノーダルは青の点線です。 | 図 6-7. 理想気体-ファンデルワールス流体混合物の \((T, x)\) 面でのスピノーダルの等圧線。 実線は相線で露点曲線は水色で、沸点曲線は青で示しています。 蒸気相のスピノーダルは水色、液相のスピノーダルは青の点線です。 |