(a)
(b)
剛体球の衝突では、2 個の剛体球は 1 回衝突して撃力を受ける(運動量の交換をする)とそのまま離れていき、 衝突と散乱は区別する必要はありません。 けれども剛体針分子同士の衝突の場合には、 分子同士が出会い、離れていく間に何度も衝突を繰り返すことがあります。 こうした衝突をガタガタ衝突 chattering collision と呼びます。 もっと複雑な V 字型や Y 字型の形状の分子であれば、 両者が絡まりあってガタガタ衝突を起こすことは考えやすいかもしれませんが、 ここで取り上げる剛体針のような単純な形状であってもガタガタ衝突が生じます。
先に衝突時刻の決定の際に考えた例を思い出していただくと、 衝突条件を満たす時刻の解が 4 つ得られ、 その中の最小の解(\(t = 1.57\))が実現されることになりました。 けれども残りの 3 つの衝突配置の解についても、(系は可逆的なので)何らかの初期条件を選べば実現されるはずです。 すると仮に 2 番目に小さな解(\(t = 1.90\))の際の衝突配置が実現したとして、 そこから出発すると最小の解(\(t = 1.57\))あるいは 3 番目に小さかった解(\(t = 2.04\))の配置で引き続き衝突が起きる、 ガタガタ衝突が発生することになります。 つまり衝突時刻の決定の際に、可能な解が複数出現することが、 ガタガタ衝突の存在を約束しているといってよいのです。
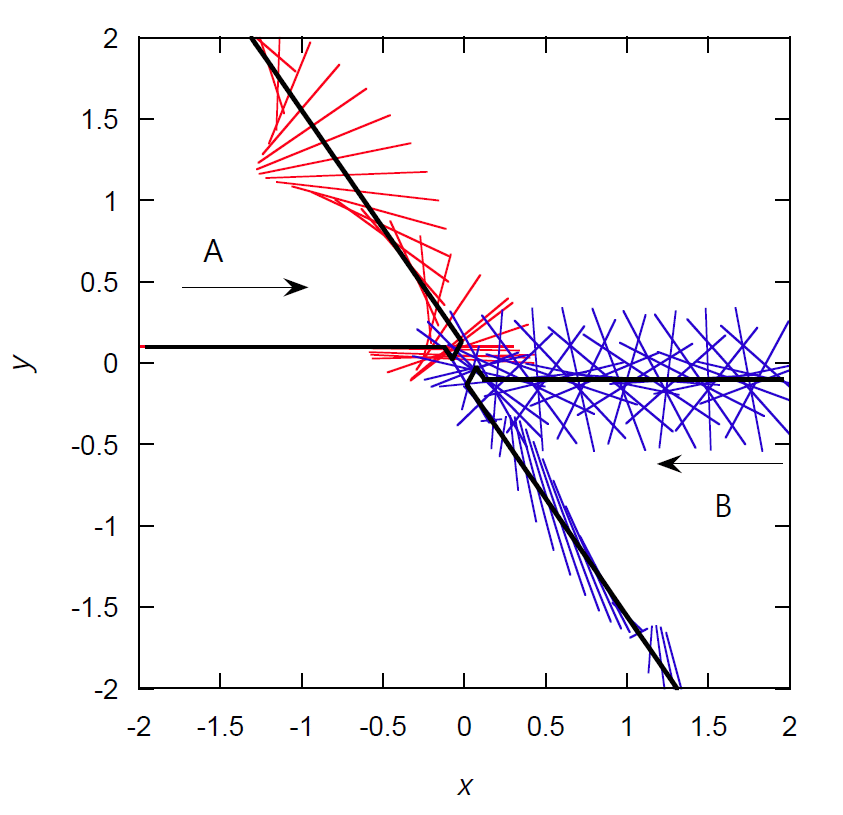
少し話が抽象的になったようなので 典型的な 2 本の剛体針のガタガタ衝突の軌道を、図 3-1 に示しましょう (ここでも換算単位系を使用します)。 先に示した衝突の軌道と同様、 2 本の針が出会いそして別れていくわけですが、 その散乱の過程は入り組んでいて、時刻 \(t\) が 3.75、3.97、4.18 で 3 回の衝突が起きています。

(a) |

(b) |
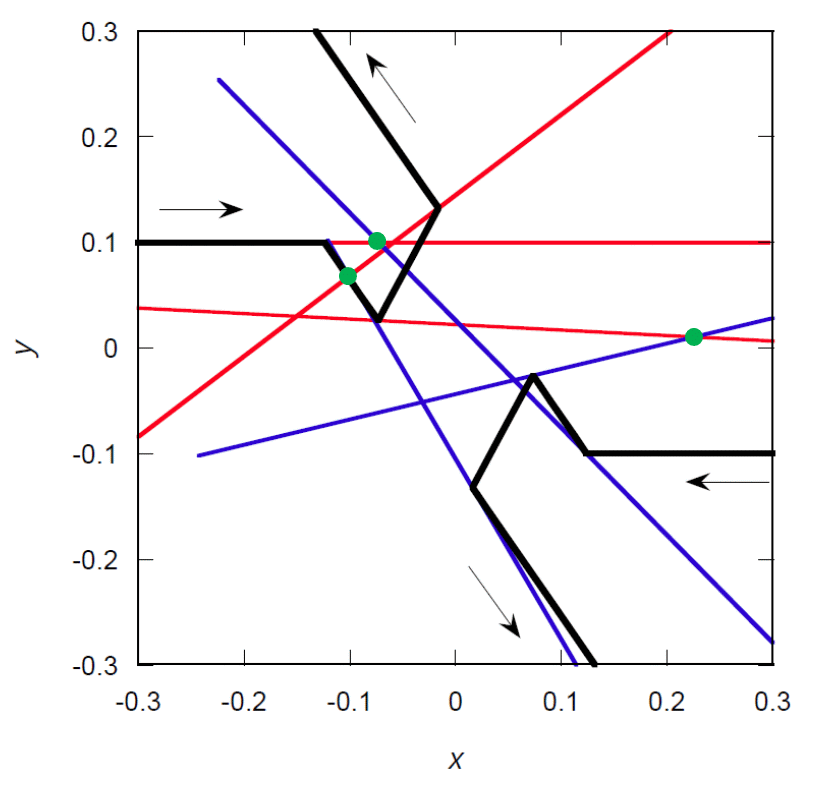
| 図 3-1. 典型的な 2 本の剛体針のガタガタ衝突の軌道の \(xy\) 面への射影。 換算単位系を用い \(m = L= T = 1\) とし、 剛体針の慣性モーメント \(I\) は 1/12。 最初 A、B 2 本の針の中心は \(xy\) 平面に \(y\) 軸から ±2.0 離れた場所に置き、それぞれ 0.5 の速さで対向して進行。 衝突パラメーターは 0.2、A、B の角速度は、 それぞれ 3.0 と 6.0 で針 A の初期の回転軸は \(y\) 軸方向を向いています。 黒い実線はそれぞれの針の中心の軌跡を示し、 時間間隔 0.1 ごと及び衝突時刻での針 A(赤線)、針 B(青線)のスナップショットを描画。 (b) は衝突の起きる近傍の拡大図で、 この散乱過程では●で示す地点で針同士の接触が起き、 3 回の衝突が起きています。 | |
|
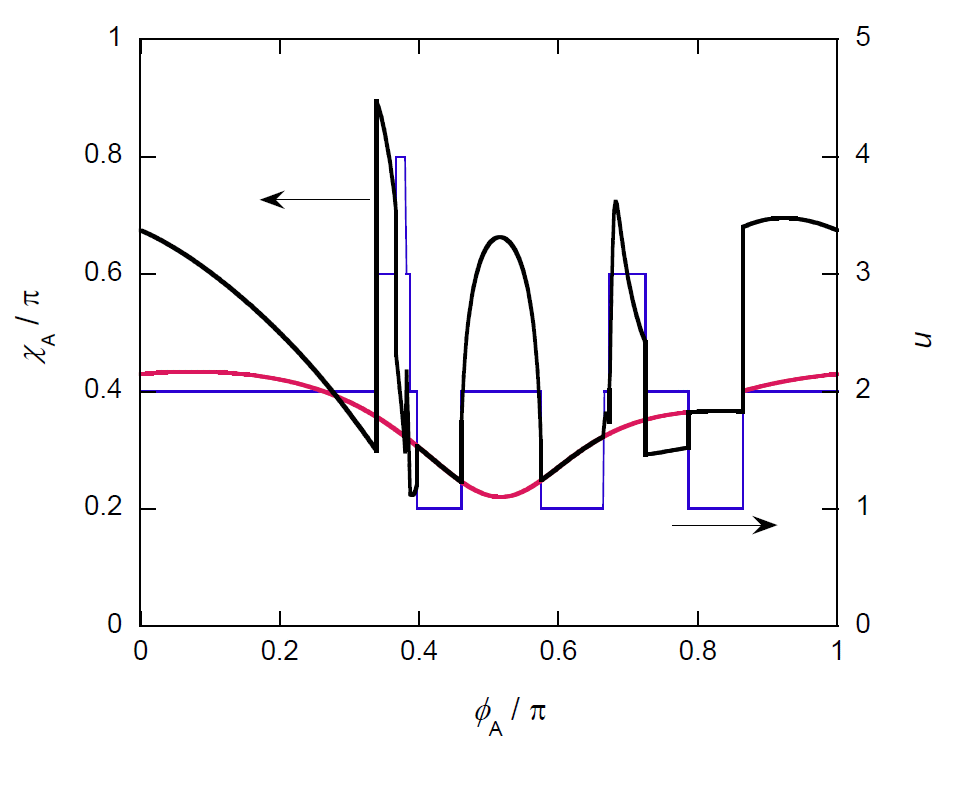
| 図 3-2. 針 A と B の間にガタガタ衝突の起きる場合の、針 A の回転の初期位相 \(\phi_\mrm{A}\) に対する散乱角 \(\chi_\mrm{A}\) の依存性。 図中、黒い実線は最終的な散乱角、赤い実線は散乱の最初の衝突による散乱角、 青い細い線は散乱の際の衝突数 \(n\)(右軸)を示します。 換算単位系を用い \(m = L= T = 1\) とし、 剛体針の慣性モーメント \(I\) は 1/12。 相対速度 1.0、衝突パラメーターは 0.3、A、B の角速度はそれぞれ 1.4 π と 0.8 π。 この衝突条件では回転の初期位相 \(\phi_\mrm{A}\) の変化にともない、 最大 4 回のガタガタ衝突が見られています。 |
先に初期条件の違いで大きな散乱挙動の変化が起きることを見ましたが、 ガタガタ衝突はそれをさらに複雑なものにします。
先に示したものと同様に、 図 3-2 には衝突する一方の針の回転の初期位相 \(\phi_\mrm{A}\) による散乱角 \(\chi_\mrm{A}\) の変化を、 ガタガタ衝突が起きる場合について示しました。 初期条件としては 2 本の針 A、B の中心は \(xy\) 平面にあり、 \(x\) 軸方向に相対速度 1.0、衝突パラメーター 0.3 で進行して衝突する想定です。 角速度は A、B それぞれ 1.4 π と 0.8 π で、 針 A の回転軸 \(\vec{j}_\mrm{A}\) は \(y\) 軸から若干 \(z\) 軸方向に傾いた方向余弦 (0, -0.95, 0.03) に、 針 B の回転軸の方向余弦は (0.48, 0.65, 0.59) に取っています。 黒い実線はそれぞれの針の中心の軌跡を示し、 図中黒い実線は A B 2 本の針が出会って離れるまでの最終的な散乱角を、 赤い実線は最初の衝突による軌道の散乱角を示しています(両者はガタガタ衝突がなければ一致)。 先に見たガタガタ衝突が起きない場合と同様、 \(\phi_\mrm{A}\) が 0.86 π で接触点が針上から外れる(\(a \gt 0.5\) となる)ことによる不連続な変化が見られますが、 ガタガタ衝突は散乱角の変動にさらに複雑な入り組んだ様相を与えます。
図 3-2 では最大 4 回のガタガタ衝突が現れ、 ガタガタ衝突の出現とともに散乱角に不連続的な変化が見られます。 ガタガタ衝突によって、散乱角は大きくなることも小さくなることもあり、 その傾向を統一的に表すことは困難です。 たとえば図の \(\phi_\mrm{A}\) が [0.34 π, 0.40 π] 付近では、 ガタガタ衝突の回数が \(\phi_\mrm{A}\) の増加とともに 2 回から 3 回、4 回 と増加し、再び 3、2 と減っています。 2 回から 3 回への増加で散乱角 \(\chi_\mrm{A}\) が 0.30 π から 0.89 π に大きく増加するものの、 その後 \(\phi_\mrm{A}\) の増加ととも散乱角は減少しガタガタ衝突の 3 回から 4 回への増加で 0.72 π から 0.45 π に不連続的に減少します。 そしてその後の 4 回から 3 回への減少に際しては散乱角は 0.30 π から 0.43 π に増加するものの、 引き続く 3 回から 2 回への減少では 0.22 π まで減っています。 なお図 3-2 で \(\phi_\mrm{A}\) 0.28 π 付近で、 最初の衝突の散乱角(赤い実線)とガタガタ衝突後の散乱角(黒い実線)が一致しています。 これはこの初期位相 \(\phi_\mrm{A}\) での 2 回のガタガタ衝突での撃力 \(P\) の方向が一致する結果で、 撃力の大きさについては、この初期位相で不連続になっています。
こうした個別のエピソードを解析していくと、 それなりのものがたりを作ることはできます。 けれどもそこから何らかの法則性なりを見出すとなると、 今のところぼくには見通しがききません。 それには何かもっと大胆に異なる視点、視座を持つ必要があるように思われます。
初期配置によっては、均質な針のガタガタ衝突が数百回にわたって持続することがあります。 そうした初期配置のパラメータ領域は非常に狭く、 また数値計算の精度にも強く依存するようになります。 こうした長く継続するガタガタ衝突の回数は、 数値計算の収束判定の設定で無論異なりますし、 計算に使用する浮動小数点数のフォーマットが単精度と倍精度でも異なります。 さらには使用する計算機の CPU によっても違ってきたりします。 これには随分悩まされました・・・
前節までに剛体針分子同士の衝突・散乱の挙動が極めて複雑で、 取り扱いが厄介なことを見ました。 けれどもそうした複雑な衝突・散乱の結果実現される、 配向や速度の平衡分布に基づいて、 剛体球の場合同様、 剛体針流体についても厳密な衝突頻度の評価が可能です。 ただし剛体球の場合に比べると、 回転運動の寄与や剛体針同士の配置の重みなどを考慮しないといけないのでいささか厄介になります。
|
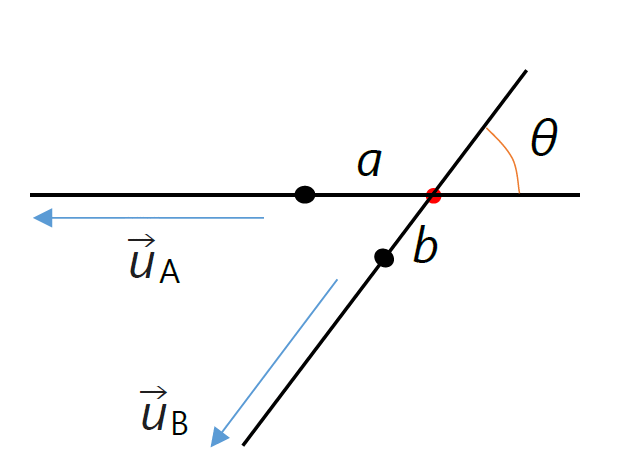
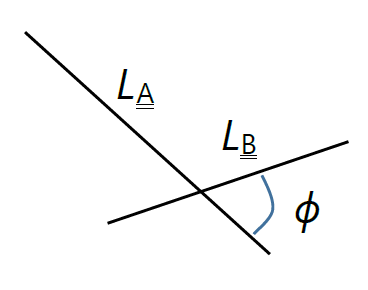
| 図 3-3. 針 A と B の衝突の際の配向。 針 A と B は衝突点(●)で、角 \(\theta\) で交わります。 |
針 A と B が衝突の配置にある状態で、 衝突点の位置 \((a, b)\) について、針に衝突する流束 \(j_\mrm{col}\) を考えます。
\begin{equation} j_\mrm{col} = \rho \avg{\vec{u}_\mrm{col} \cdot \vec{v}_{ab}}_{-} \label{eq:colflux} \end{equation}
ここで \(\vec{u}_\mrm{col}\) は接触している針 A と B で作られる平面に垂直な単位ベクトル(法線ベクトル)で、 \(\vec{v}_{ab}\) は針 A の接触位置から針 B の接触位置を見た時の相対速度です:
\begin{equation} \vec{v}_{ab} = (\vec{v}_\mrm{B} - \vec{v}_\mrm{A}) - (a \vec{\omega}_\mrm{A} \x \vec{u}_\mrm{A}) + (b \vec{\omega}_\mrm{B} \x \vec{u}_\mrm{B}) \label{eq:relvelab} \end{equation}
また式 \eqref{eq:colflux} で \(\avg{~~}_{-}\) と添え字に \(-\) を付けているのは、 相対速度の法線方向成分の A に向かうものについて平均することを示しています。
先の剛体球分子の場合、分子の並進運動だけを考え、衝突の流束は”分子の流れ”のように見なせました。 剛体針分子の衝突の流束では、分子の”各部位の流れ”を考える必要があり、分子の回転速度も関わってきます。 この式 \eqref{eq:colflux} で表される流束は 3 次元のマクスウェル分布に従い、 並進の相対速度 \(\vec{v}_\mrm{r}\)(\(= \vec{v}_\mrm{B} - \vec{v}_\mrm{A}\))、 針 A の角速度 \(\vec{\omega}_\mrm{A}\)、針 B の角速度 \(\vec{\omega}_\mrm{B}\) それぞれの、針 A と B で作られる平面の法線方向(\(\vec{u}_\mrm{col}\))成分からなっています。 剛体球の場合には、1 次元の並進運動(式 \eqref{eq:relvelab} の右辺第 1 項)で話が済みました。 この場合には衝突点によって分散が異なる(\(a, b\) に依存する)、3 次元のマクスウェル分布なので少し複雑です。 速度分布を考慮して接触点での衝突の流束 \(\avg{j_\mrm{col}}_{a,b}\) を求めると、次式のようになります:
\begin{equation} \avg{j_\mrm{col}}_{a,b} = \rho \sqrt{\frac{T}{\pi}} \sqrt{\frac{1}{m} + \frac{a^2 + b^2}{2I}} \label{eq:colfluxth} \end{equation}
この流束を針 A と B のさまざまな衝突配置について足しこんでやれば、衝突頻度が求まりますが、 この手続きも少し厄介です。 針 A と B のなす角を \(\theta\) として(\(0 \le \theta \lt \pi\))、 この配置での衝突頻度を求めると、 流束の断面積は \(|\vec{u}_\mrm{A} \x \vec{u}_\mrm{B}| = \sin \theta\) に比例しますから、 衝突頻度は次式で評価できます:
\begin{equation} Z(\theta) = \sin \theta \int_{-L/2}^{L/2} \rmd a \int_{-L/2}^{L/2} \rmd b ~2 \avg{j_\mrm{col}}_{a,b} = \sin \theta \rho \sqrt{\frac{T}{\pi m}} \frac{32 I}{3m L^2} F_{3/2}(8I/mL^2) \label{eq:colfreq1} \end{equation}
ここで \(2 \avg{j_\mrm{col}}_{a,b}\) と流束を 2 倍にしているのは、衝突の配置で表と裏、2 方向の流束を考慮する必要があるためです。 また \(F_n (x)\) は次式で表される関数です:
\begin{equation} F_n(x) \equiv \int_{0}^{\pi/4} \rmd \phi \left[ \lpar{1 + \frac{1}{x \cos^2 \phi}}^n -1 \right] \label{eq:fnx} \end{equation}
2 本の直線が \(\theta\) で交わる確率は \(\sin \theta\) に比例しますから、 \(Z(\theta)\) の \(\theta\) についての平均を取って、衝突頻度の表現を得ます:
\begin{equation} Z = \frac{\int_0^{\pi} \sin \theta ~Z(\theta) ~\rmd \theta}{\int_0^{\pi} \sin \theta ~\rmd \theta} = \frac{\rho L^2}{3} \sqrt{\frac{\pi T}{m}} \frac{8 I}{m L^2} F_{3/2}(8I/mL^2) \label{eq:colfreq} \end{equation}
均質な針であれば、慣性モーメント \(I = mL^2/12\) ですから衝突頻度は、 次式のようになります:
\begin{equation} Z(I = mL^2 / 12) = \frac{2}{9} \rho L^2 \sqrt{\frac{\pi T}{m}} F_{3/2}(2/3) = 0.698276\ldots \rho L^2 \sqrt{\frac{\pi T}{m}} \label{eq:colfreq_homo} \end{equation}
流体の分子動力学シミュレーションでも、式 \eqref{eq:colfreq_homo} の成立は確認されています。 またモンテカルロ法で初期配置を 1 × 106 回発生させた弾道計算も行ってみたのですが、 式 \eqref{eq:colfreq_homo} の係数は 0.701 ± 0.003 で一致していました。 剛体球気体の衝突頻度 \(Z_\mrm{HS}\) は次式のようになっていますから、 剛体球の直径と同じ長さの均質な剛体針では、 衝突頻度が剛体球の場合の 6 分の 1 程度になっているわけです。
\begin{equation} Z_\mrm{HS} = 4 \rho \sigma^2 \sqrt{\frac{\pi T}{m}} \label{eq:colfreq_hs} \end{equation}
丸々した剛体球が ”痩せて” 針になったら、 互いの衝突が起きにくくなるというのは直観的にうなづけます。 けれども話はそれほど単純ではありません。 式 \eqref{eq:colfreq} で、剛体針の慣性モーメントを小さくしていくと、 \(F_{3/2} (x)\) は \(x \to 0\) で \(x^{-3/2}\) に比例するようになるので、 衝突頻度は慣性モーメントの平方根の逆数に比例して、いくらでも大きくなるのです。 これは回転運動が激しくなり、ガタガタ衝突の頻度が増すことを意味します。
衝突頻度については、厳密な表式が得られました。 それでは 2 本の針が出会い、何らかの相互作用(衝突)を行って別れる頻度、 散乱の頻度はどうでしょうか? 散乱の頻度を考える上では、ともかく 2 本の針が出会って衝突すればよく、 その後に 2 本の針の間に何らかの相互作用(衝突)が起きても考慮の対象にはなりません。 つまりガタガタ衝突について考えなくてよいのです。 ガタガタ衝突を考慮しなくてよいことは、 問題を簡単にしてくれるようにも見えます。 けれども散乱頻度の場合には、 接触配置での流束ではなく、 2 本の針が衝突配置に到達するまでの流束を評価することになるので、 問題はより厄介になります。
図 3-4 には、針 A から見た針 B の衝突の際の概念図を示しました。 簡単のため針 B の回転軸が、 針 A の中心と相対速度ベクトル \(\vec{v}_\mrm{r}\) の載った平面の法線方向を向いているとします。 この回転軸の向きでは、針 B は針 A の中心で衝突することになりますが、 実線で示した方位で入射した場合、回転運動がなければ衝突(散乱)は起きません。 けれども回転運動があれば、B が A の近傍を通過するのに要する時間を \(\tau\) とすると、 A の近くを通過する間に針 B の向きが \(\omega_\mrm{B} \tau\) 程度変化し、 衝突が起きるようになります。 衝突する方位で入射した針が衝突しなくなる効果もあるので、 角度 \(\omega_\mrm{B} \tau\) が十分小さければ特段の変化は起きませんが、 角度が大きくなってくると、正負どちらに回転しても衝突が起きやすくなります。 こうした問題を A と B の様々な配置について考慮しないといけないのですが、 衝突していない配置から衝突を経ずに衝突の配置に至る確率を計算する問題、 時間相関の関わる問題になるので、 ある時刻における衝突の配置だけを問題にすればよかった衝突頻度の問題に比べて格段に困難が増します。
散乱頻度については、こうした分子近傍を通過する間の回転運動の問題があってちょっと手の付けようがないのですが、 慣性モーメントが極めて大きい時と極めて小さい時、 回転しないと考えてよい場合と回転速度が大きい極限については、 厳密な評価が可能です (慣性モーメントが大きく \(I \gt mL^2/4\) の場合には、 質量分布が針の外部にあふれ出ることになりますが、 ここではそうした場合も許容します)。
|
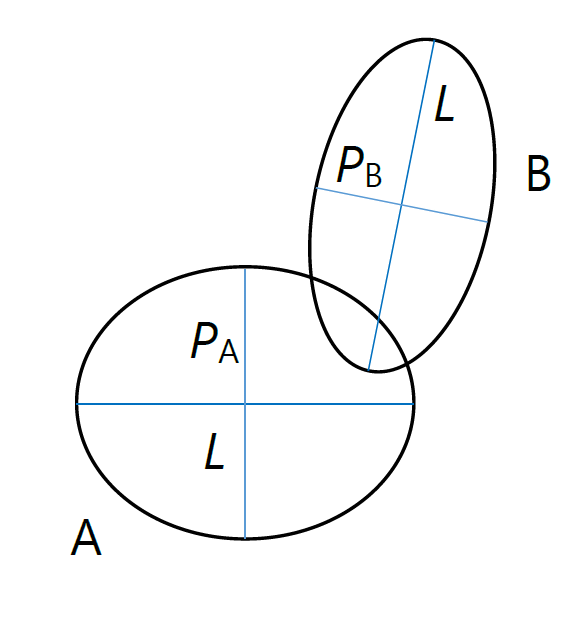
| 図 3-5. 針 A と針 B の相対速度ベクトル \(\vec{v}_\mrm{r}\) に垂直な平面に対する射影。 針の回転を無視できる場合には、 散乱断面積は A と B の射影が交わる配置を、 全方位について平均化したものになります。 |
慣性モーメントが極めて大きくて、 散乱の過程における針の回転運動が無視できる場合については比較的簡単です。 図 3-4 のような A と B の相対的な運動を考え、 相対速度ベクトル \(\vec{v}_\mrm{r}\) に垂直な平面への、 針 A と B の射影を考えます。 針の回転が起きない場合には、 A と B の衝突が起きる場合には射影された A と B の図形は交わり、 A と B の射影が交わる配置の面積を A と B の配向について平均化したものが散乱断面積になります。
射影面上で針 A と B が長さ \(L_\mrm{A}\) と\(L_\mrm{B}\) の針が、 さまざまな角度 \(\phi\) で重なり合う配置について平均した 散乱断面積 \(s\) は次式で得られます:
\begin{equation} s = \frac{1}{\int_0^{\pi} \phi ~\rmd \phi} \int_0^{\pi} (L_\mrm{A} L_\mrm{B} \sin \phi) ~\rmd \phi = \frac{2}{\pi} L_\mrm{A} L_\mrm{B} \label{eq:csll0} \end{equation}
ここで A と B の針の射影の長さの平均 \(\avg{L}_\mrm{proj}\) を考えると、 相対速度ベクトル \(\vec{v}_\mrm{r}\) に対して、 針の向き \(\vec{u}\) が \(\theta\) 傾いているとすると、 射影の長さは \(L \sin \theta\) です。 極座標を考え、天頂角 \(\theta\) について平均を取ると、次式のようになります:
\begin{equation} \avg{L}_\mrm{proj} = \frac{1}{\int_0^{\pi} \sin \theta ~\rmd \theta} \int_0^{\pi} (L \sin \theta) \sin \theta~ \rmd \theta = \frac{\pi}{4} L \label{eq:prjl} \end{equation}
最終的に平均化された散乱断面積 \(\avg{s}\) は次式のように与えられます:
\begin{equation} \avg{s} = \frac{2}{\pi} \avg{L_\mrm{A}}_\mrm{proj} \avg{L_\mrm{B}}_\mrm{proj} = \frac{\pi}{8} L^2 \label{eq:csll} \end{equation}
こうして得られる針の回転運動が無視できる場合の散乱頻度 \(Z_\mrm{scat}(I \to \infty)\) は次のようになります:
\begin{equation} Z_\mrm{scat}(I \to \infty) = \avg{s} \avg{|\vec{v_\mrm{r}}|} \rho= \frac{\pi}{8} L^2 ~4 \sqrt{\frac{T}{\pi m}}~ \rho = \frac{1}{2} \rho L^2 \sqrt{\frac{\pi T}{m}} \label{eq:scatfreq_sn} \end{equation}
これは先の衝突頻度の式 \eqref{eq:colfreq} で \(I \to \infty\) の極限を取ったものと一致します。
|
図 3-5. 慣性モーメントが極めて小さい針 A と B の相対速度ベクトル \(\vec{v}_\mrm{r}\) に垂直な平面に対する射影。 針が高速回転しているので A と B は回転軸の固定された円盤としてふるまい、 その射影は長径が \(L\)、短径 \(p\) の楕円になります。 この楕円が重なる A と B の配置の面積が、散乱断面積に相当します。 |
慣性モーメントが極めて小さい時、 針はある軸の周りを回転する直径 \(L\) の円盤のように見なせます。 回転しない針の場合同様に、\(\vec{v}_\mrm{AB}\) を法線とする面に対する射影を取ると、 この円盤は長径が \(L\) 短径 \(p\) の楕円としてふるまいます。 楕円 A と B が接触する配置についての面積を、 すべての配向について平均化したものが、 慣性モーメントが極めて小さい針の散乱断面積を与えることになります。
こうした図形の重なりに関わる測度の問題は、 古くから積分幾何学・幾何的確率論と呼ばれる分野で研究されてきました。 ある平面上で楕円が重なり合う配置の面積は、 凸体についての積分幾何の主公式から次式で得られます (積分幾何の主公式では、全体の回転についても積分を取ることになるので、 ここで考慮する面積 \(s\) の \(2\pi\) 倍になります):
\begin{equation} 2 \pi s = C_\mrm{A} C_\mrm{B} + 2\pi (S_\mrm{A} + S_\mrm{B}) \label{eq:funeq_blaschke} \end{equation}
ここで \(C\) は楕円の周の長さ、\(S\) は楕円の面積です。
先の 2 本の針の重なりの問題では、 面積 \(S\) が 0 で、周長 \(C\) が \(2 \avg{L}_\mrm{proj}\) の楕円を考えることになり、 式 \eqref{eq:funeq_blaschke} からただちに式 \eqref{eq:csll} を得ることができます。
楕円の短軸の長さを \(p\) とすると 針の回転軸方向についての平均 \(\avg{p}_\mrm{proj}\) は次のようになります(式 \eqref{eq:prjl} との相違に注意):
\begin{equation} \avg{p}_\mrm{proj} = \frac{1}{\int_0^{\pi/2} \sin \theta ~\rmd \theta} \int_0^{\pi/2} (L \cos \theta) \sin \theta ~\rmd \theta = \frac{1}{2} L \label{eq:minorax_av} \end{equation}
ですから射影面の楕円の面積 \(S = (\pi/4) Lp\) の平均は次式のように書けます:
\begin{equation} \avg{S}_\mrm{proj} = \frac{\pi}{4} L \avg{p}_\mrm{proj} = \frac{\pi}{8} L^2 \label{eq:elips_av} \end{equation}
楕円の周の長さは第2種楕円積分になっていささか厄介ですが、 針の回転軸方向についての平均を取ると、 次式のように簡単になります:
\begin{equation} \avg{C}_\mrm{proj} = \frac{\pi^2}{4} L \label{eq:elipc_av} \end{equation}
これら楕円の面積と周長についての結果を式 \eqref{eq:funeq_blaschke} に入れると、 平均化された散乱断面積 \(\avg{s}\) は次式のようになり:
\begin{equation} \avg{s} = \lpar{\frac{\pi^3}{32} + \frac{\pi}{4}} L^2 \label{eq:cs_eli} \end{equation}
ここから得られる散乱頻度は以下のようになります:
\begin{equation} Z_\mrm{scat}(I \to 0) = \avg{s} \avg{|\vec{v_\mrm{r}}|} \rho = \lpar{1 + \frac{\pi^2}{8}} \rho L^2 \sqrt{\frac{\pi T}{m}} \label{eq:scatfreq_eli} \end{equation}
これは回転しない針の場合(式 \eqref{eq:scatfreq_sn})に比べて \(2 + \pi^2/4 = 4.4674\ldots\) 倍で、 剛体球の場合と比較すると \(0.558425\ldots\) 倍です。 なおモンテカルロ法で初期配置を 5 × 105 回発生させた弾道計算も行ってみたのですが、 散乱頻度は剛体球の場合の 0.559 ± 0.001 倍となり、 一致することを確認しています。
剛体針気体中の 1 本の剛体針の衝突と散乱の頻度について見ましたが、 ガタガタ衝突のため衝突頻度は散乱頻度より大きくなります。 慣性モーメント \(I\) が小さくなり回転速度が増すと、 衝突頻度は \(1/\sqrt{I}\) に比例していくらでも大きくなり(式 \eqref{eq:colfreq})、 一方散乱頻度は大きくはなるものの有限値に止まります(式 \eqref{eq:scatfreq_eli})。 つまりガタガタ衝突は慣性モーメントが小さくなると、どんどん増加していくわけです。 このことは、図 3-4 で見たように、 2 本の針が接近して通り過ぎるまでの間に \(\omega \tau\) 程度の回転をし、 それに応じてガタガタ衝突が起きると考えれば、 角速度 \(\omega\) の大きさは慣性モーメントの平方根に反比例するので、 定性的には理解できます。
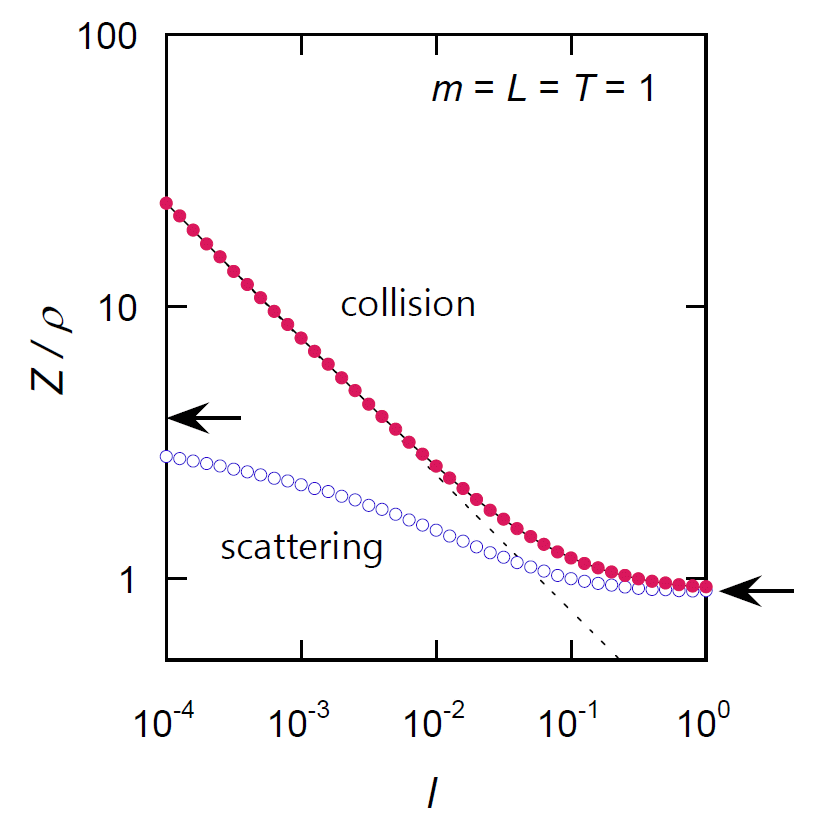
こうした描像を確認するため、慣性モーメント \(I\) を変化させ、 弾道計算を行って散乱と衝突の頻度を計算した結果を図 3-6 に示します。 換算単位系を用い \(m = L= T = 1\) としています。 慣性モーメントの大きい極限では、散乱と衝突の頻度は一致しています。 慣性モーメントを小さくしていくにしたがって、 散乱と衝突の頻度は大きくなっていきますが、 両者の比 \(Z/Z_\mrm{scat}\) は慣性モーメント \(I = 1\) で 1.03、\(I = 0.1\) では 1.19、 \(I = 0.01\) で 1.72、\(I = 0.001\) で 3.46 となっています。 均一な針(\(I = 1/12\))では 1.21 で、ガタガタ衝突はそう頻繁に起きているわけではありませんが、 無視できない頻度で起きています。
|
図 3-6. 散乱頻度(黒)と衝突頻度(赤)の慣性モーメント依存性。 弾道計算による結果(それぞれの慣性モーメントについて 1 × 106 の弾道をランダムに発生させて計算)。 換算単位系を用い \(m = L= T = 1\) としています。 図には衝突頻度の理論値(式 \eqref{eq:colfreq})も黒い実線で書き込んでいますが、 弾道計算の結果と重なっていて明瞭に見えていません。 対数スケールで描いており、図中の破線は衝突頻度の \(I \to 0\) での漸近式に対応していて勾配は -0.5 です。 また図中の矢印は、 散乱頻度の慣性モーメントの大きい極限(式 \eqref{eq:scatfreq_sn})と小さい極限(式 \eqref{eq:scatfreq_eli})の値を示しています。 |