まずはよく知られた、剛体球分子からなる気体中での衝突のはなしから始めましょう。 後述の剛体針の場合との比較もあって、その衝突の条件などを少し細かく見てみます。
剛体球からなる数密度 \(\rho\) の気体を考えます。 剛体球は完全弾性体で、質量 \(m\)、 直径 \(\sigma\) で表面がツルツルである(衝突の際に偶力が働かず、回転運動を考慮する必要がない)とします。
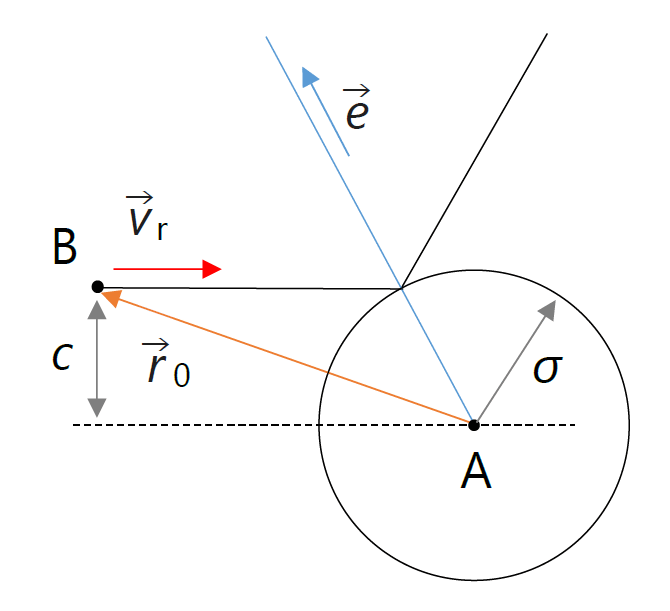
さて2個の剛体球 A と B がそれぞれ運動しているとき、 A から見た B の軌道 \(\vec{r}_\mrm{AB}(t)\) は次のように表されます:
\begin{equation} \vec{r}_\mrm{AB}(t) = \vec{r}_\mrm{B}(t) - \vec{r}_\mrm{A}(t) = \vec{r_0} + \vec{v}_\mrm{r} t \label{eq:reltra} \end{equation}
ここで、\(\vec{v}_\mrm{r}\) は B の A に対する相対速度 \(\vec{v}_\mrm{B} - \vec{v}_\mrm{A}\)、 \(\vec{r_0}\) は \(t = 0\) での相対位置です。 この2つの剛体球が時刻 \(t\) で衝突する場合、AB 間の距離は \(\sigma\) になっているので、次の関係が成立します:
\begin{equation} |\vec{r_0} + \vec{v}_\mrm{r} t| = \sigma \label{eq:colcond} \end{equation}
この衝突の時刻 \(t\) は、次の2次方程式の根で与えられます:
\begin{equation} \vec{v}^2_\mrm{r} t^2 + 2 (\vec{r}_0 \cdot \vec{v}_\mrm{r}) t + \vec{r}_0^2 - \sigma^2 = 0 \label{eq:colcond2} \end{equation}

|
| 図 1-1. 剛体球同士の衝突。 剛体球 A から見た B の軌道の様子。 衝突パラメータ \(c\) が球の直径 \(\sigma\) より小さく、 \(\vec{r}_0 \cdot \vec{v}_\mrm{r} \lt 0\) の時、衝突が起きる・ |
衝突が起きる場合には \(t\) は実根を持ち、 判別式から次の関係が成り立つ必要があります:
\begin{equation} (\vec{r}_0 \cdot \vec{v}_\mrm{r})^2 - \vec{v}^2_\mrm{r}(\vec{r}_0^2 - \sigma^2) \ge 0 \label{eq:det} \end{equation}
この式は \(\vec{r}_0\) と \(\vec{v}_\mrm{r}\) のなす角を \(\theta\) とすると、 \(\vec{r}_0 \cdot \vec{v}_\mrm{r} = |\vec{r}_0| |\vec{v}_\mrm{r}| \cos \theta\) ですから、 次のように書き換えることができます:
\begin{equation} \sigma^2 \ge \vec{r}_0^2 \sin^2 \theta = c^2 \label{eq:colparam} \end{equation}
ここで \(c\) はいわゆる衝突パラメーターです (歴史と伝統で記号 \(b\) がもっぱら使用されますが、ここでは \(c\) とします)。 また \(t\) が負だと過去に衝突したことがあるという話になるので、 \(t \gt 0 \) であるためには次の条件が必要です:
\begin{equation} \vec{r}_0 \cdot \vec{v}_\mrm{r} \lt 0 \label{eq:direct} \end{equation}
この2つの条件は、図で示せば直観的にも明らかです。 A から見た時の B の軌道の直線(式 \eqref{eq:reltra})と点 A で作られる平面を考えると、 衝突は A と B の軌道の間の距離 \(c\) (衝突パラメーター)が、 球の直径 \(\sigma\) より小さい時に起きます(式 \eqref{eq:colparam})。 また衝突するには、軌道上を A に接近する方向で B が運動するわけで、 それが式 \eqref{eq:direct} に示されています。
衝突の際の運動の変化について見ておくと、 衝突が起きた時、撃力(インパルス)\(P\) が生じます。 剛体球は完全弾性体で表面がツルツルであると考えているので、 撃力は2個の剛体球の接触面に垂直に働きます。 A から B に向かう単位ベクトルを \(\vec{e}\) とすると、 A に働く撃力は次式で表されます:
\begin{equation} \vec{P} = m (\vec{v}_\mrm{r} \cdot \vec{e}) \vec{e} \label{eq:impulse} \end{equation}
衝突前後で A から見た B の軌道は折れ曲がるわけですが、 点 A と衝突前後の A から見た B の軌道は、同じ平面上にあります(角運動量の保存)。 衝突後の A、B それぞれの速度 \(\vec{v}'_\mrm{A}\)、 \(\vec{v}'_\mrm{B}\) は次のようになります:
\begin{eqnarray} \vec{v}'_\mrm{A} &=& \vec{v}_\mrm{A} + \vec{P}/m \label{eq:newva} \\ \vec{v}'_\mrm{B} &=& \vec{v}_\mrm{B} - \vec{P}/m \label{eq:newvb} \end{eqnarray}
速度の \(\vec{e}\) 方向成分を考えると、反発係数が 1、 A と B の速度成分の交換が起きることになります。
|
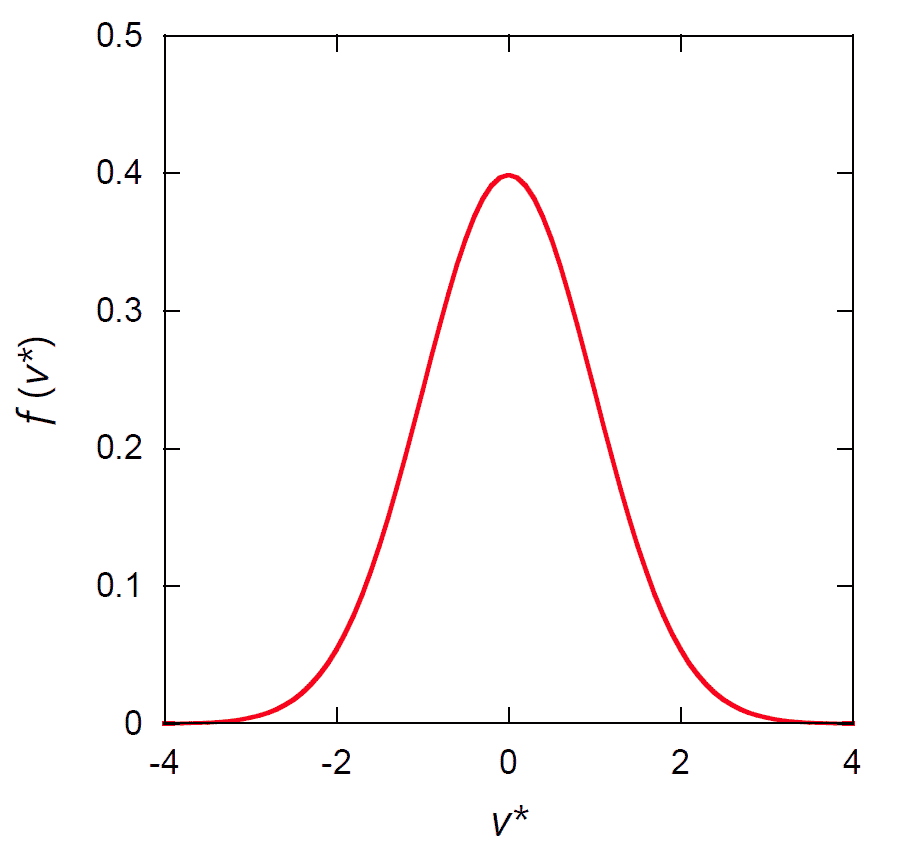
| 図 1-2. マクスウェルの速度分布関数(1 次元)。 \(v^* = v/\sqrt{T/m}\) として描いているので、標準正規分布 N(0, 1) と一致します。 |
熱力学温度 \(T\) の平衡状態で、分子の速度分布はマクスウェル分布に従い、 ある軸に沿った(1 次元の)速度 \(v\) の分布関数(確率密度)は次式で与えられます:
\begin{equation} f(v) = \sqrt{\frac{m}{2 \pi T}} \exp \lpar{-\frac{mv^2}{2T}} \label{eq:maxweld} \end{equation}
このおはなしでは全編通じて、式を簡明にするために、ボルツマン定数 \(k_\mrm{B}\) を 1 とし、熱力学温度 \(T\) はエネルギーであるとします。 ここで考える剛体球気体では系を特徴づける質量、単位となる質量 \([\mrm{M}]\) は剛体球の質量 \(m\) であり、 単位となる長さ \([\mrm{L}]\) は剛体球の直径 \(\sigma\) と取ることができます。 温度 \(T\) は系のエネルギーの単位 \([\mrm{E}]\) を与え、 \([\mrm{E}] = [\mrm{M}] [\mrm{L}]^2 [\mrm{T}]^{-2}\) の関係から、系の時間の単位 \([\mrm{T}]\) を次式で与えることができます:
\begin{equation} [\mrm{T}] = [\mrm{L}] \sqrt{[\mrm{M}] [\mrm{E}]^{-1}} = \sigma \sqrt{m/T} \label{eq:redunitt} \end{equation}
実際の分子についてどの程度のオーダーになるか評価してみると、 アルゴン(原子量 40)など想定すると、質量は 7 × 10-26 kg、原子の直径は 0.4 nm 程度ですから、 温度が 300 K( ≈ 4 × 10-21 J)程度とすると、 \([\mrm{T}]\) は 2 ps 程度になります。 また速度 \([\mrm{L}]/[\mrm{T}]\) は 200 m/s 程度です。
マクスウェル分布は、 密度や場所、あるいは分子間相互作用に依存しません。 ですから分子同士が遠く離れていても、 あるいは接近した状態でも、 平衡状態では速度分布に違いはありません (強い力が働くようになると量子力学的な取り扱いが必要になりますが、このおはなしでは考慮しません)。
さてマクスウェル分布は、平均が 0 で分散 \(\avg{v^2}\) が \(T/m\) のガウス分布(正規分布)になっています。 ガウス分布に従う独立な2変数の和あるいは差はやはりガウス分布に従い、 その分散は両者の和になります。 ですから先に考えた A と B の相対速度 \(\vec{v}_\mrm{r}\) は、A と B が独立に運動しているなら、 やはりガウス分布に従い、相対速度 \(\vec{v}_\mrm{r}\) のある軸に沿っての速度成分 \(v_\mrm{r}\) の分散は1個の分子の速度の分散の2倍になります (相対速度と重心速度で記述する立場では、換算質量が \(m/2\) であるためとして説明されます):
\begin{equation} \avg{v^2_\mrm{r}}= \avg{(v_\mrm{B} - v_\mrm{A})^2} = \avg{v^2_\mrm{A}} + \avg{v^2_\mrm{B}} = \frac{2T}{m} \label{eq:rvvar} \end{equation}
また速度の大きさの平均 \(\avg{|v|}\) は次のようになり:
\begin{eqnarray} \avg{|v|} &=& \int_{-\infty}^{\infty} {|v| f(v) \rmd v} = 2 \sqrt{\frac{m}{2 \pi T}} \int_{0}^{\infty} {v \exp \lpar{-\frac{mv^2}{2T}} \rmd v} \nonumber \\ &=& \sqrt{\frac{2T}{\pi m}} \label{eq:speed} \end{eqnarray}
相対速度の大きさの平均 \(\avg{|v_\mrm{r}|}\) は、 式 \eqref{eq:rvvar} のように分散が 2 倍になるので(あるいは換算質量が 1/2 になるので)\(\sqrt{2}\) 倍になります:
\begin{equation} \avg{|v_\mrm{r}|}= 2 \sqrt{\frac{T}{\pi m}} \label{eq:relspeed} \end{equation}
ここまである軸方向、1 次元の速度を見てきましたが、 よく知られている 3 次元の速度の大きさの平均 \(\avg{|\vec{v}|}\) は次のようになります:
\begin{equation} \avg{|\vec{v}|}= \int_{-\infty}^{\infty} |\vec{v}| f(\vec{v}) ~\rmd \vec{v} = \sqrt{\frac{m}{2 \pi T}}^3 \int_{0}^{\infty} v^3 \exp \lpar{-\frac{mv^2}{2T}} 4 \pi \rmd v = \sqrt{\frac{8T}{\pi m}} \label{eq:speed3d} \end{equation}
です。 また 3 次元での相対速度の大きさの平均 \(\avg{|\vec{v}_\mrm{r}|}\) は、1 次元の場合同様 \(\sqrt{2}\) 倍になります:
\begin{equation} \avg{|\vec{v}_\mrm{r}|}= 4 \sqrt{\frac{T}{\pi m}} \label{eq:relspeed3d} \end{equation}
ここまで並進運動について見てきましたが、 分子の回転運動についても同様に、ある慣性モーメント \(I\) の主軸周りの角速度 \(\omega\) は、 次のようなマクスウェル分布に従います:
\begin{equation} f(\omega) = \sqrt{\frac{I}{2 \pi T}} \exp \lpar{-\frac{I \omega^2}{2T}} \label{eq:maxweldrot} \end{equation}
剛体分子同士の衝突頻度を評価するのに、 初歩の気体分子運動論のおはなしで、 単位時間あたりに断面積 \(\pi \sigma^2\) の分子が掃く体積中の分子数を考えて、 それが単位時間当たりの衝突数に相当するといった話がよく出てきます。 ここではまず、さまざまな状況の剛体分子にも適用できる一般的な導出を紹介しましょう。
流体中で、ある面の正方向に流入してくる分子の流束 \(j_{+}\) は次式で表されます:
\begin{equation} j_{+} = \rho \avg{v_{+}} \label{eq:flux} \end{equation}
ここで \(\rho\) は面上の分子の数密度、\(\avg{v_{+}}\) は分子の法線方向に向かう速度成分の平均です。
|
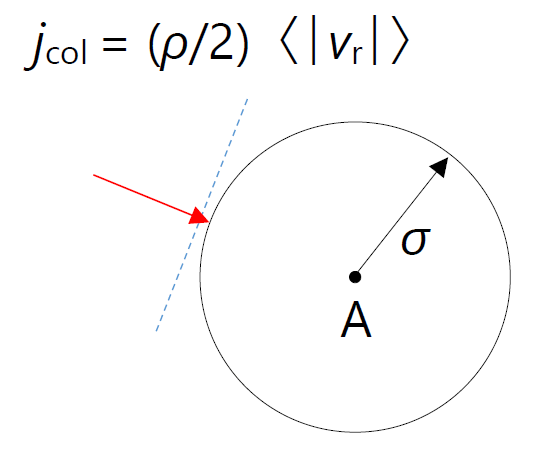
| 図 1-3. 剛体球分子 A への衝突の流束。 衝突は剛体球分子 A を中心とする半径 \(\sigma\) の球(排除球)の面上で起き、 衝突地点へ向かう分子の流束は \((\rho/2) \avg{|v_\mrm{r}|}\) になります。 |
ある分子 A に他の分子が衝突する頻度を評価するには、 図 1-3 のように分子 A を中心とする半径 \(\sigma\) の球面への分子の出入りを考えればよいのです。 球面上では衝突が起き、分子は撃力を感じることになりますが、 それぞれの分子の速度分布はマクスウェル分布に従います。 ただし注意しないといけないのは、分子 A も運動していることです。 ですから式 \eqref{eq:flux} の分子の平均速度 \(\avg{v_{+}}\) は、A に対する相対的な速度の平均を取る必要があります。 また半分の粒子は反対方向に運動しており、先の式 \eqref{eq:relspeed} から、 衝突する流束 \(j_\mrm{col}\) は次式で評価できます:
\begin{equation} j_\mrm{col} = \rho \frac{1}{2} \avg{|v_\mrm{r}|}= \rho \sqrt{\frac{T}{\pi m}} \label{eq:colflux} \end{equation}
ある剛体球分子 A の衝突頻度 \(Z_\mrm{HS}\) は、球面全体について流入する流量を求めればよく、次式で与えられます:
\begin{equation} Z_\mrm{HS} = 4 \pi \sigma^2 j_\mrm{col} = 4 \pi \sigma^2 \rho \sqrt{\frac{T}{\pi m}} \label{eq:colfreq} \end{equation}
この式がよく知られたマクスウェルが導いた衝突頻度の式
\begin{equation} Z_\mrm{HS} = \pi \sigma^2 \rho \avg{|\vec{v}_\mrm{r}|} \label{eq:colfreqx} \end{equation}
と一致していることは容易に確認いただけるでしょう(式 \eqref{eq:relspeed3d} 参照)。 マクスウェルの取り扱いでは、 剛体球の排除球の断面積 \(\pi \sigma^2\) に入射してくる流束 \(\rho \avg{|\vec{v}_\mrm{r}|}\) で、 衝突頻度を評価していることになっています。 剛体球の場合にはこの断面積(散乱断面積)が明白ですが、 剛体分子に異方性があるとなかなか厄介です。 この点、後で取り上げるように、剛体分子同士の接触配置での流束を考える方が、 (やさしくはありませんが)まだしも取り扱いが容易です。
なお剛体球気体の密度 \(\rho\) が高くなると、 玉突きよろしく種々の相関が生じて衝突頻度が変化しますが、 それは球面上の平衡密度(平衡における密度相関)の問題として扱えます。
余談ですが、衝突頻度の問題とも関わって、 平均自由行程については 19 世紀来さまざまに検討されました。 今日の初歩の物理化学の教科書に登場する平均自由行程はマクスウェルが導入したもので、 \(\avg{|\vec{v}|}/Z\) で表され、ある分子が引き続く衝突の間に進む距離の平均に相当します。 この扱いで、衝突数を考える時は相対速度なのに、それで 1 個の分子の平均速度を割るという操作に、 戸惑いを感じる人も多いでしょう。 この取り扱いでは、一連の衝突間の行程が、すべて同じ重みで評価されています。 けれども自由行程の速度依存性を考慮して、 平均自由行程を評価すると異なる結果が得られます。 平均自由行程の問題は、Enskog や Chapman たちの取り扱いの出現する以前には、 気体の粘度など輸送係数の評価の上でも大きな位置を占め、 ボルツマンの「気体論講義」(1896)(Dover から英訳が出ています)などには、 こうした話題が盛んに取り上げられています。