無限に細い（太さのない）剛体針からなる気体の場合も、 剛体球の場合と同様に系を特徴づける長さは針の長さだけで、 系の熱力学的な記述は（排除体積が 0 なので剛体球以上に）単純です。 けれども分子運動に目を転じれば、 剛体球では考える必要のなかった回転運動、分子の配向を考慮する必要があり、 格段に複雑な挙動を取り扱うことになります。
|
|
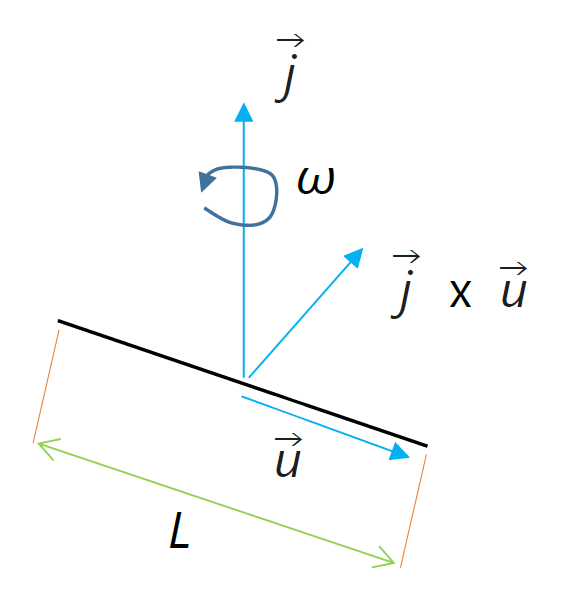
| 図 2-1. 無限に細い剛体針。 \(\vec{u}\) は針の長さ方向の、\(\vec{j}\) は回転軸方向の単位ベクトル。 |
もっとも単純な ”形” を持った剛体分子のモデルとして、 図 2-1 のような剛体針を考えます。 針の長さを \(L\)、針の質量を \(m\) とし重心は針の中心にあるものとし、 針は無限に細く、針の軸の周りの回転は起きないものとします。 また先の剛体球でもそうでしたが、針はツルツルで、 力は針の長さに対し垂直方向にしか働かないとします。
針の長さ方向に沿う単位ベクトルを \(\vec{u}\) とし、 \(\vec{u}\) に垂直な回転軸の周りを角速度 \(\omega\) で回転運動をするとします。 回転軸に沿う単位ベクトルを \(\vec{j}\) とすると、角速度ベクトル \(\vec{\omega}\) は \(\omega \vec{j}\)、 針の回転は次式で表せます：
\begin{equation} \vec{u}(t) = \vec{u}(0) \cos \omega t + [\vec{j} \x \vec{u}(0)] \sin \omega t \label{eq:rotation} \end{equation}
もし針が超高速で回転しておれば、 針は面の法線方向が \(\vec{j}\) に固定された直径 \(L\) の円盤と見なすこともできます。
針の中心の垂直方向の慣性モーメント \(I\) は、 針が均質であれば \((1/12) mL^2\) になります：
\begin{equation} I = \int_{-L/2}^{L/2} (m/L) r^2 \rmd r = \frac{1}{12}mL^2~~~~\mbox{均質な針} \label{eq:minert_homo} \end{equation}
このおはなしでは、もっぱらこうした均質な針を扱いますが、 質量が中心付近に分布するもっと慣性モーメントの小さい針や、 またいささか”非物理的”ですが極めて慣性モーメントが大きく回転しない針を考えることもできます。
先に剛体球気体の物理量の単位の与え方を見ましたが、 剛体針についても同様に、 単位となる長さ \([\mrm{L}]\) として剛体針の長さ \(L\) を取り、 単位となる時間 \([\mrm{T}]\) も温度 \(T\) をエネルギーの単位 \([\mrm{E}]\) に用い、 次式で評価することで単位系を構成できます：
\begin{equation} [\mrm{T}] = [\mrm{L}] \sqrt{[\mrm{M}] [\mrm{E}]^{-1}} = L \sqrt{m/T} \label{eq:redunitt} \end{equation}
剛体針の場合には、 並進運動だけでなく回転運動も関わってきますが、 角速度 \(\omega\) の単位は \([\mrm{T}]^{-1}\) ですし、 慣性モーメントの単位は \([\mrm{M}][\mrm{L}]^2 = mL^2\) に取ればよいわけです。 以下に示す計算結果では、特に断らない限りこの単位系（換算単位系と呼びます）を用います。
現実系を念頭に、少し具体的に慣性モーメント \(I\) と角速度 \(\omega\) について見ておくと、 仮に分子量が 50（\(m\) ≈ 8 × 10-24 kg） で針の長さが 0.5 nm だとすると、均質な針であれば慣性モーメントは 1.7 × 10-45 kg m2 になります（式 \eqref{eq:minert_homo}）。 また 300 K（≈ 4 × 10-21 J）での角速度を \(\sqrt{T/I}\) で評価するとおよそ 1.6 × 1012 rad/s です（振動数は 0.25 THz）。 窒素分子 N2 の慣性モーメントは 1.4 × 10-46 kg m2、 塩素分子 Cl2 であれば 1.2 × 10-45 kg m2 ですから、そう現実離れしたものではありません。
|
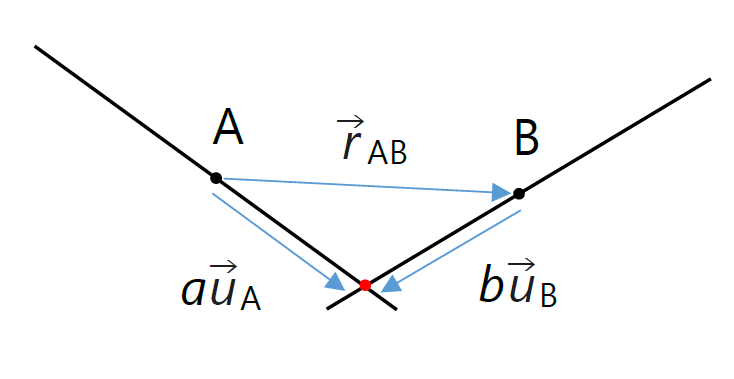
| 図 2-2. 針 A と B が衝突する瞬間の配置。 針 A と B は同一平面上にあり、衝突点は A の中心から \(a\)、 B の中心から \(b\) の位置にある。 |
剛体球の衝突の場合には、中心間距離をモニターしておればよかったわけですが、 剛体針同士の衝突の扱いの場合には、どの配置で衝突するかを決める必要があります。
2 本の針 A と B が、図のような配置で衝突した瞬間を考えます。 この時 2 本の針は同一平面上にあり、 2 本の針の中心を結ぶベクトルを \(\vec{r}_\mrm{AB}\) とすると、 次の関係が成り立っています：
\begin{equation} a \vec{u}_\mrm{A} - b \vec{u}_\mrm{B} - \vec{r}_\mrm{AB} = 0 \label{eq:colcond} \end{equation}
ここで \(a\)、\(b\) は、Ａ、B それぞれの針の中心からの衝突点の位置です。
この条件を満たすには、まず 2 本の針が同一平面上にあることから、 3 つのベクトル \(\vec{u}_\mrm{A}\)、\(\vec{u}_\mrm{B}\)、\(\vec{r}_\mrm{AB}\) の３重積 \(f\) が 0 である必要があります：
\begin{equation} \mbox{☆}~~~f = (\vec{u}_\mrm{A} \x \vec{u}_\mrm{B}) \cdot \vec{r}_\mrm{AB} = 0 \label{eq:grassmann} \end{equation}
また針の衝突点の位置は、\(a\) については式 \eqref{eq:colcond} から
\begin{equation} a (\vec{u}_\mrm{A} \x \vec{u}_\mrm{B}) - \vec{r}_\mrm{AB} \x \vec{u}_\mrm{B} = 0 \label{eq:colposax} \end{equation}
であることから、
\begin{equation} a (\vec{u}_\mrm{A} \x \vec{u}_\mrm{B})^2 = (\vec{r}_\mrm{AB} \x \vec{u}_\mrm{B}) \cdot (\vec{u}_\mrm{A} \x \vec{u}_\mrm{B}) = [\vec{u}_\mrm{B} \x (\vec{u}_\mrm{A} \x \vec{u}_\mrm{B})] \cdot \vec{r}_\mrm{AB} = [\vec{u}_\mrm{A} - (\vec{u}_\mrm{A} \cdot \vec{u}_\mrm{B}) \vec{u}_\mrm{B}] \cdot \vec{r}_\mrm{AB} \label{eq:colposay} \end{equation}
より、ベクトルの内積を用いて \(a\) を表すと次式のようになります：
\begin{equation} a = \frac{\vec{u}_\mrm{A} \cdot \vec{r}_\mrm{AB} - (\vec{u}_\mrm{A} \cdot \vec{u}_\mrm{B}) (\vec{u}_\mrm{B} \cdot \vec{r}_\mrm{AB})} {1 - (\vec{u}_\mrm{A} \cdot \vec{u}_\mrm{B})^2} \label{eq:colposa} \end{equation}
同様に \(b\) は次のように表されます：
\begin{equation} b = -\frac{\vec{u}_\mrm{B} \cdot \vec{r}_\mrm{AB} - (\vec{u}_\mrm{A} \cdot \vec{u}_\mrm{B}) (\vec{u}_\mrm{A} \cdot \vec{r}_\mrm{AB})} {1 - (\vec{u}_\mrm{A} \cdot \vec{u}_\mrm{B})^2} \label{eq:colposb} \end{equation}
2 本の針が衝突する時、衝突地点は針上にないといけませんから、衝突には次の条件が必要です：
\begin{equation} \mbox{☆}~~~|a| \le L/2 ~~~ \mbox{and} ~~~ |b| \le L/2 \label{eq:within} \end{equation}
こうして針の衝突の条件式が、☆印をつけた式 \eqref{eq:grassmann} と式 \eqref{eq:within} で、 形の上では出そろったことになります。 2 本の針が衝突するかどうか、衝突するとしていつ、どのような配置で衝突するかを知るには、 式 \eqref{eq:grassmann} から \(f(t) = 0\) となる時刻 \(t\)（\(\gt 0\)）を求め、 その時刻における衝突地点が針上にあるかどうか（式 \eqref{eq:within} を満たすかどうか）を調べればよいわけです。
|
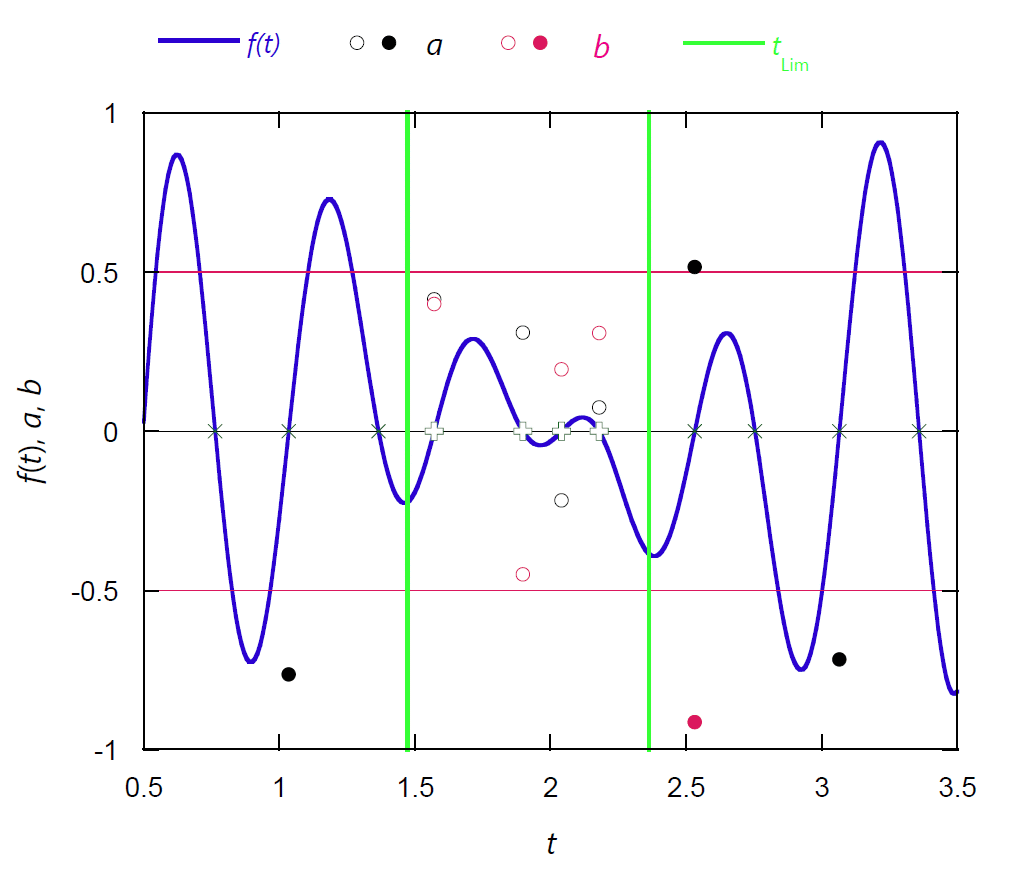
| 図 2-3. 典型的な、剛体針 A B 間のベクトル 3 重積 \(f(t)\) の時間変化（図中の青線） と接触点 \(a\)（黒丸）と \(b\)（赤丸）の計算値 （ ✕ 及び塗りつぶした丸は、衝突条件を満たさない \(f(t)=0\) の解に対応）。 換算単位系で \(m = L= T = 1\) とし、 剛体針の慣性モーメント \(I\) は 1/12、 衝突パラメーターは 0.2、相対速度は 1 で、剛体針 A、B の角速度は、 それぞれ 1.5 π と 2 π。 図中黄緑の線は解の存在領域 \(t_\mrm{Lim}\) の上限、下限で、 \(\vec{j}_\mrm{A}\)、\(\vec{j}_\mrm{B}\) を回転軸とする、 直径 \(L\) の円盤の同士の接触時間から算出したもの。 この領域 \(t_\mrm{Lim}\) の中の ➕ で示す 4 つの \(f(t) = 0\) の解は、 接触条件を満たして衝突時間の候補となり、その中の最小のものが実際に実現する衝突。 |
しかし \(f(t)\) は激しく振動する関数で、 式 \eqref{eq:grassmann} の解を求めるにはニュートン法などの数値計算によるしかなく、 また解は一般に無数に存在します。 ですからまず条件式 \eqref{eq:within} を満たすような解の存在領域 \(t_\mrm{Lim} = [t_\mrm{L}, t_\mrm{U}]\) を得てから、 適切な初期値を設定して \(t_\mrm{Lim}\) 内で式 \eqref{eq:grassmann} の解（\(t \gt 0\)）を探索し、 その解の中で式 \eqref{eq:within} を満たす最小の値を得るという手続きを踏むことになります。 たぶんもっとも簡単な解の存在領域 \(t_\mrm{Lim}\) の取り方は、 剛体針 A B の中心間の距離 \(|\vec{r}_\mrm{AB}|\) が、針の長さ \(L\) より小さくなる時間領域に取るもので、 先の剛体球の衝突条件の取り扱いにならって決める方法です。 けれども（ここでは詳しく触れませんが）少し手間はかかりますが、\(\vec{j}_\mrm{A}\)、\(\vec{j}_\mrm{B}\) を回転軸とする、 直径 \(L\) の円盤の同士の接触時間を求める方が、より狭い \(t_\mrm{Lim}\) が得られ、 解の探索の効率を上げることができます （\(t_\mrm{Lim}\) の設定について Frenkel たちはもう少し簡易な手法を取っています）。
図 2-3 には典型的な関数 \(f(t)\) の挙動と、剛体針の衝突時間の決定について示します（換算単位系を用いています）。 図では初期 \(t = 0\) で、剛体針 A から \(x\) 軸に沿って相対距離 2.0 離れた地点から、 \(x\) 軸に沿って相対速度 \(\vec{v}_\mrm{r}\) 1.0 で剛体針 B を衝突させています。 衝突パラメーターは 0.2 に取っています。 A、B はそれぞれ角速度 1.5 π と 2 π で回転しており、 （回転軸の配向などの詳細は省略しますが、） \(f(t)\) には式 \eqref{eq:grassmann} に見るように角速度 \(\omega_\mrm{A} \pm \omega_\mrm{B}\) で振動する要素が絡み合い、 激しく振動する様子が見て取れるでしょう。
ここから衝突時刻を求めるわけですが、 図には \(f(t) = 0\) の解の中で時点で計算される接触位置の値 \(a\) と \(b\) を \(\circ\) で示してあります。 式 \eqref{eq:within} を満たさないもの（±0.5 以内にならないもの）は塗りつぶしてあり、 \(f(t) = 0\) の解の中で、条件を満たさないものは ✕ で、 満たすものを ➕ で表しました。 この初期配置からえられる衝突時刻としては 4 つあるわけですが、 実際に初期配置から始めて衝突が実現するのは、その中の（\(t \gt 0\) で）最小の解（\(t = 1.57\)）ということになります。 なお図には円盤同士の接触時間から求めた、解の存在領域 \(t_\mrm{Lim}\) [1.47, 2.36] も示してあります。 球の接触時間からは [1.02, 2.98] になるので、 解の探索領域を大幅に狭めることができ、 またこの \(t_\mrm{Lim}\) 内で得られる\(f(t) = 0\) の解は、 式 \eqref{eq:within} を満たします。
|
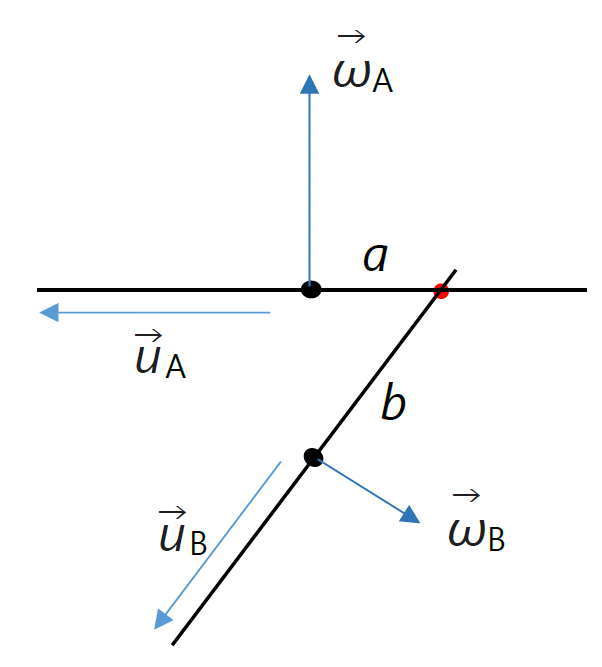
| 図 2-5. 剛体針 A と B の衝突時の配向。 衝突時 A と B が載っている平面の法線方向の単位ベクトルを \(\vec{u}_\mrm{col}\) とします。 |
衝突が起きるかどうか、どのような配置で起きるのかについて見たわけですが、 衝突の際にどのような力（撃力）が働き、どう運動が変化するのかを見ておきましょう。
衝突時の剛体針 A と B の配向の様子を図 2-5 に示します。 針 B が針 A に及ぼす撃力を \(\vec{P}\) とすると、 剛体針は表面がツルツルであるとしているので、 衝突の際の撃力は針と針の接触点（図中 •）に、2 本の針の作る平面に垂直方向に働きます。 撃力の大きさを \(P\) とすると、 撃力は衝突時 A と B が載っている平面の法線方向の単位ベクトル \(\vec{u}_\mrm{col}\)
\begin{equation} \vec{u}_\mrm{col} = \frac{\vec{u}_\mrm{A} \x \vec{u}_\mrm{B}}{|\vec{u}_\mrm{A} \x \vec{u}_\mrm{B}|} \label{eq:impulvec} \end{equation}
を用いて次式で表せます：
\begin{equation} \vec{P} = P ~\vec{u}_\mrm{col} \label{eq:impul1} \end{equation}
さて A と B の運動量には運動量保存の法則から \(\pm \vec{P}\) の変化が生じるので、 衝突後の速度を ' を付けて表すと、次式が成立します：
\begin{equation} m \vec{v}'_\mrm{A} = m \vec{v}_\mrm{A} + \vec{P}, ~~~ m \vec{v}'_\mrm{B} = m \vec{v}_\mrm{B} - \vec{P} \label{eq:momcons} \end{equation}
また角運動量には角運動量保存の法則から、 力のモーメントだけの変化が生じます：
\begin{equation} I \vec{\omega}'_\mrm{A} = I \vec{\omega}_\mrm{A} + (a \vec{u}_\mrm{A} \x \vec{P}), ~~~ I \vec{\omega}'_\mrm{B} = I \vec{\omega}_\mrm{B} - (b \vec{u}_\mrm{B} \x \vec{P}) \label{eq:angmomcons} \end{equation}
さてエネルギーの保存の法則から次式が成り立ちます：
\begin{equation} \frac{m}{2}(\vec{v}^2_\mrm{A} + \vec{v}^2_\mrm{B}) + \frac{I}{2}(\vec{\omega}^2_\mrm{A} + \vec{\omega}^2_\mrm{B}) =\frac{m}{2}[(\vec{v}_\mrm{A} + \vec{P}/m)^2 + (\vec{v}_\mrm{B} - \vec{P}/m)^2] + \frac{I}{2} \left[ (\vec{\omega}_\mrm{A} + a \vec{u}_\mrm{A} \x \vec{P}/I)^2 + (\vec{\omega}_\mrm{B} - b \vec{u}_\mrm{B} \x \vec{P}/I)^2 \right] \label{eq:econserv} \end{equation}
ここで \(\vec{\omega} \cdot (\vec{u} \x \vec{P}) = \vec{P} \cdot (\vec{\omega} \x \vec{u})\) であることなどに注意すると次式が得られ、
\begin{equation} \lpar{\frac{1}{m} + \frac{a^2 + b^2}{2I}} P^2 =\vec{P} \cdot (\vec{v}_\mrm{B} - \vec{v}_\mrm{A}) + \vec{P} \cdot [-(a \vec{\omega}_\mrm{A} \x \vec{u}_\mrm{A}) + (b \vec{\omega}_\mrm{B} \x \vec{u}_\mrm{B})] \label{eq:impx} \end{equation}
撃力の大きさ \(P\) は次式で与えられます：
\begin{equation} \lpar{\frac{1}{m} + \frac{a^2 + b^2}{2I}} P = \vec{u}_\mrm{col} \cdot \vec{v}_{ab} \label{eq:impulse} \end{equation}
ここで \(\vec{v}_{ab}\) は次式で与えられる針 A の接触位置から針 B の接触位置を見た時の相対速度です：
\begin{equation} \vec{v}_{ab} = [\vec{v}_\mrm{B} + (b \vec{\omega}_\mrm{B} \x \vec{u}_\mrm{B})] -[\vec{v}_\mrm{A} + (a \vec{\omega}_\mrm{A} \x \vec{u}_\mrm{A})] \label{eq:relvelab} \end{equation}
こうして衝突する時刻と衝突による運動の変化の表式が得られたところで、 実際にどのような衝突の様子が観察されるかを見てみましょう。 最初 A、B 2 本の針の中心を \(xy\) 平面に \(y\) 軸から等距離に置き、 それぞれ 0.5 の速さで対向して進むようにしています（重心は静止しているわけです）。 先の剛体球同士の衝突であれば \(xy\) 平面上で話が済みますが、 剛体針の場合には、衝突の際に \(z\) 軸方向の成分が生まれ、話は単純ではなくなります。 なお換算単位系を用い \(m = L= T = 1\) とし、 剛体針の慣性モーメント \(I\) は 1/12（均質な針）にしています。
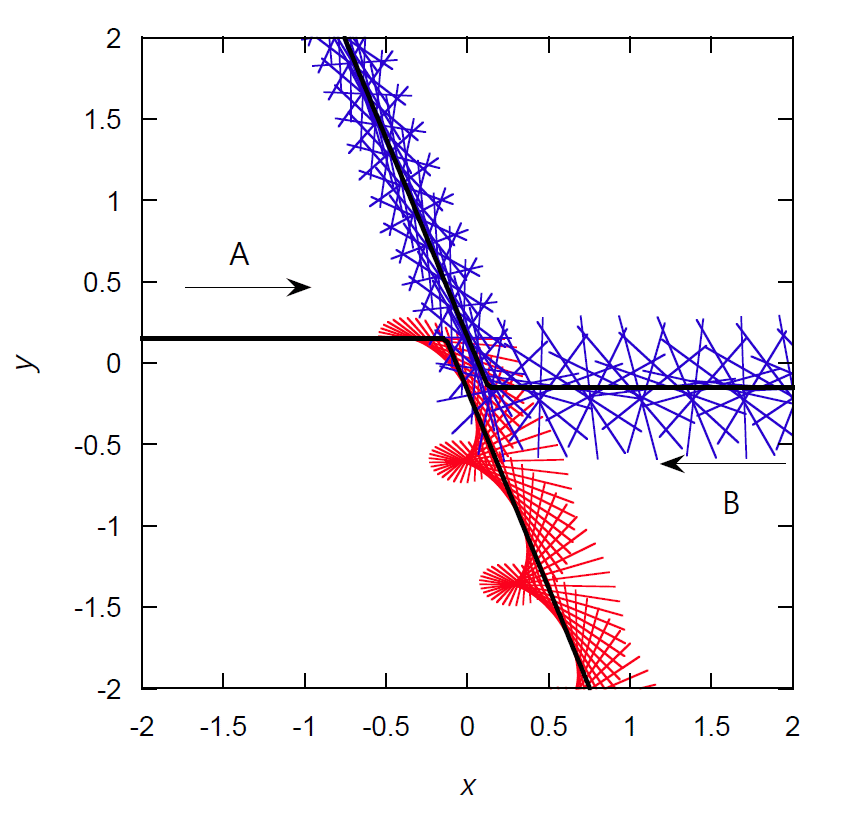
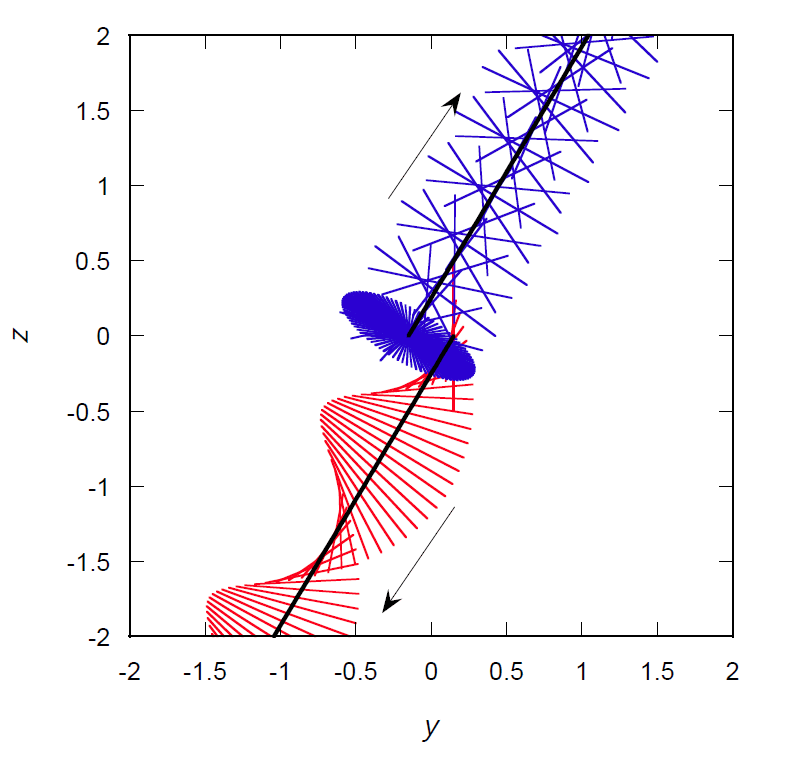
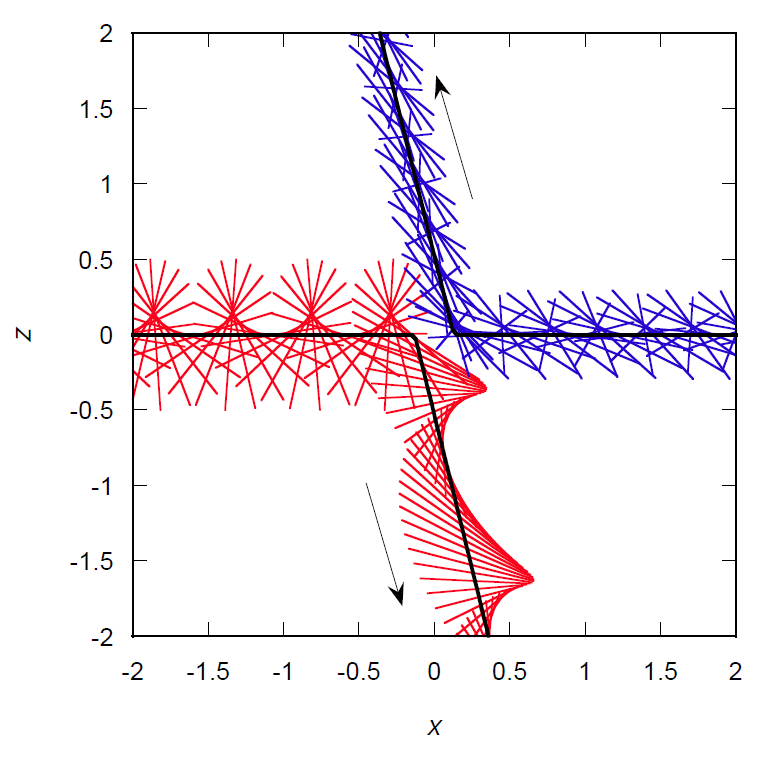
図 2-4 に示すのは A、B の角速度をそれぞれ 3.0 と 5.0 として、 衝突パラメーター 0.3 で衝突させた時の運動の軌跡を、 \(xy\)、\(yz\)、\(zx\) 平面にそれぞれ投影したものです。 黒い実線はそれぞれの針の中心の軌跡を示し、 赤線で針 A の、青線で針 B の、時間間隔 0.1 ごとのスナップショットを描いています。 条件の詳細は煩雑になるので省略しますが、 針 A の初期の回転軸を \(y\) 軸方向に取っているので、衝突までは \(xy\) 平面上の針 A の姿が見えていません。
回転運動の変化をともないながら、 分子衝突によって針は \(z\) 方向にも散乱されていきます。 衝突によって針 A の並進の速さは、0.5 から 0.64 に増加し、 その運動の軌跡は角度にして 0.43 π rad 変化します。 針 B の並進運動にも同様の変化が起きます（式 \eqref{eq:momcons}）。 また針 A の角速度 \(\omega_\mrm{A}\) は 3.0 から 1.32 に、 針 B の角速度 \(\omega_\mrm{B}\) は 5.0 から 5.34 にそれぞれ変化し、 A の回転軸 \(j_\mrm{A}\) は 0.43 π rad、B の回転軸 \(j_\mrm{B}\) は 0.19 π rad それぞれ傾きます。
(a) |
(b) |
(c) |
| 図 2-4. 典型的な 2 本の剛体針の衝突の軌跡。 (a) は \(xy\) 平面、(b) は \(yz\) 平面、(c) は \(zx\) 平面への射影。 換算単位系を用い \(m = L= T = 1\) とし、 剛体針の慣性モーメント \(I\) は 1/12。 最初 A、B 2 本の針の中心は \(xy\) 平面に \(y\) 軸から等距離に置き、それぞれ 0.5 の速さで対向して進行 （重心は動かない設定）。 衝突パラメーターは 0.3、A、B の角速度は、 それぞれ 3.0 と 5.0。 黒い実線はそれぞれの針の中心の軌跡を示し、 赤線で針 A の、青線で針 B の、時間間隔 0.1 ごとのスナップショットを描画。 針 A の初期の回転軸は \(y\) 軸方向に取っています。 この散乱過程では 1 回の衝突のみが起きています。 | ||
野球のバットや木の枝などを投げた時にも経験することですが、 剛体針の衝突の軌道は、わずかな初期値の違いで大きく変化します。 図 2-5 には、衝突する剛体針 A の回転の初期位相を \(\phi_\mrm{A}\) 変えた（\(\vec{u}^{*}(0)\) は基準とする初期方位）
\begin{equation} \vec{u}_\mrm{A}(0) = \vec{u}^{*}(0) \cos (\phi_\mrm{A}) + [\vec{j}_\mrm{A} \x \vec{u}^{*}(0)] \sin (\phi_\mrm{A}) \label{eq:rotationx} \end{equation}
ことによる、典型的な (a) 運動の軌跡と (b) 散乱角 \(\chi_\mrm{A}\)
\begin{equation} \cos \chi_\mrm{A} = \frac{\vec{v}_\mrm{A} \cdot \vec{v}'_\mrm{A}}{|\vec{v}_\mrm{A}| |\vec{v}'_\mrm{A}|} \label{eq:scatang} \end{equation}
の変化を示します。 回転の位相の少しの違いで、運動の軌跡に大きな変動が現れますが（図 2-5a）、 図 2-5b の散乱角 \(\chi_\mrm{A}\) の変化に注目してみると、 回転位相の変化とともに不連続な変化が何回か起きていることが分かります。 この場合、\(\phi_\mrm{A}\) が 0.09 π、0.48 π、0.59 π で \(\chi_\mrm{A}\) の不連続な変化が起き、 そこでは接触点の位置（\(a\)、\(b\)）にも不連続な変化が見られます。 この不連続な変化は、接触点の位置が針上から外れる（条件式 \eqref{eq:within} を満たさなくなる） ことで生み出されています。 図 2-5a で示した軌跡では、この不連続的な変化を挟んだ領域の初期位相で見ているので、 非常に大きな変化が現れたわけです。 棒を投げたりするのに例えれば、 「当たり所が悪い（良い）」と思わぬところに跳ね返るようなものです。 なお図 2-5 では見られませんが、不連続な変化は、 針同士が同一平面上から外れる（条件式 \eqref{eq:grassmann} を満たさなくなる）ことでも生じます。
(a) |
|
|
図 2-5.
針 A と B の衝突において、針 A の回転の初期位相 \(\phi_\mrm{A}\) を変化させた時の軌跡の変化。
図 2-4. と同様の初期配置ですが、
衝突パラメーターは 0.4、A、B の角速度は、
それぞれ 0.6 π と 0.9 π にしており、針の回転軸や初期位相は異なります。
この条件では A の回転の位相 \(\phi_\mrm{A}\) を変化させても、衝突は 1 回だけです。
(a) 針 A の回転の初期位相 \(\phi_\mrm{A}\) を 0.4 π、0.5 π、0.6 π 変化させた時の軌跡の \(xy\) 面への射影。 3 種類の軌跡を重ね書きしているので、絵が詰まないように図 2-4 の 2 倍の時間間隔 0.2 ごとのスナップショットで示しています。 針 B については初期条件を変えていないので、 衝突までの針 B スナップショットは同じですが、 A については初期位相が異なるのでスナップショットが少しずつずれています。 (b) 散乱角 \(\chi_\mrm{A}\) の変化。 図中、細い実線は A（赤）、B（青）の針上の衝突位置 \(a\) と \(b\)（図 2-2）を示します。 \(\phi_\mrm{A}\) が π 変化するのは、針 A の向きの反転が起きることに相当し、 \(a\) については符号が反転しますが、散乱角と \(b\) は [0, π] 区間同様の変動をします。 \(\phi_\mrm{A}\) の変化とともに接触点の位置が変化し、針上から外れる（条件式 \eqref{eq:within} を満たさなくなる） とともに不連続な変化が現れています。 | |