剛体針流体中の衝突頻度の計算は結構厄介で、 Frenkel たちもかなり苦戦したようです。 また散乱頻度については、ガタガタ衝突を正しく評価する必要があり、 一般的な場合については（ぼくには）絶望的で、\(I \to 0\) （円盤同士の散乱）と \(I \to \infty\)（ランダム配向の回転しない針の散乱） についての結果を得るにとどまっています。 ここでは少しその詳細を紹介しておきます。
剛体針分子の衝突については 衝突点の位置 \((a, b)\) における衝突の流束 \(j_\mrm{col}\) を考えます。
\begin{equation} j_\mrm{col}= \rho \avg{\vec{u}_\mrm{col} \cdot \vec{v}_{ab}}_{-} \end{equation}
\(j_\mrm{col}\) は A の方向の速度成分を取るので下付き - を付けています。 ここで \(\vec{v}_{ab}\) は、 並進の相対速度 \(\vec{v}_\mrm{r} = \vec{v}_\mrm{B} - \vec{v}_\mrm{A}\)、針 A の回転速度 \(\vec{\omega}_\mrm{A} \x \vec{u}_\mrm{A}\)、 針 B の回転速度 \(\vec{\omega}_\mrm{B} \x \vec{u}_\mrm{B}\) の 3 つの成分からなっています：
\begin{equation} \vec{v}_{ab} = \vec{v}_\mrm{r} - a (\vec{\omega}_\mrm{A} \x \vec{u}_\mrm{A}) + b (\vec{\omega}_\mrm{B} \x \vec{u}_\mrm{B}) \label{eq:relvelab} \end{equation}
並進の相対速度は分散が \(2T/m\) の 3 次元のマクスウェル分布、 A と B の回転速度 \(\vec{\omega} \x \vec{u}\) は回転軸 \(\vec{j}\) に垂直な面内の分散 \(T/I\) の 2 次元のマクスウェル分布になります。 これら 3 つからなる運動の衝突方向の成分 \(\vec{u}_\mrm{col} \cdot \vec{v}_{ab}\) を考えることになるので、 まずマクスウェル分布を標準化して取り扱いを容易にするために、次のベクトル \(\vec{p}\) と \(\vec{q}\) を考えましょう：
\begin{eqnarray} \vec{p} &=& (\sqrt{\frac{m}{2T}} v_\mrm{r}, \sqrt{\frac{I}{T}} \omega_\mrm{A}, \sqrt{\frac{I}{T}} \omega_\mrm{B}) = (p_1, p_2, p_3) \\ \vec{q} &=& (\sqrt{\frac{2T}{m}}, \sqrt{\frac{T}{I}} a , \sqrt{\frac{T}{I}} b) = (q_1, q_2, q_3) \end{eqnarray}
\(\vec{p}\) は 3 次元の標準ガウス分布に従うので、その分布関数は次式で表されます：
\begin{equation} f(\vec{p}) = \sqrt{\frac{1}{2 \pi}}^3 \exp{\lpar{-\frac{\vec{p}^2}{2}}} \end{equation}
AB 面に垂直な方向の速さは、\(\vec{p}\) と \(\vec{q}\) の内積で表され、 衝突の速度成分は次式で表されます：
\begin{equation} (\vec{u}_\mrm{col} \cdot \vec{v}_{ab})_{-} = (\vec{p} \cdot \vec{q})_{-} = p q \cos \theta ~~~~ (0 \le \theta \le \pi/2 ) \end{equation}
ここで \(p = |\vec{p}|\)、\(q = |\vec{q}|\) とし、\(\theta\) は 2 つのベクトル \(\vec{p}\) と \(\vec{q}\) のなす角で、 \(\vec{q}\) の向きは \(\vec{u}_\mrm{col}\) と一致するようにしています。 \(q\) は次式のように書け
\begin{equation} q = \sqrt{2T} \sqrt{\frac{1}{m} + \frac{a^2 + b^2}{2I}} \end{equation}
接触位置はそのままにして、 \(j_\mrm{col}\) を \(\vec{p}\) について平均を取ると次のようになります：
\begin{eqnarray} \avg{j_\mrm{col}}_{a,b} &=& \rho q \int_0^{\pi/2} \rmd \theta \int_0^\infty (p \cos \theta) f(\vec{p}) 2 \pi \sin \theta ~p^2 ~\rmd p \nonumber \\ &=& \rho \sqrt{2T} \sqrt{\frac{1}{m} + \frac{a^2 + b^2}{2I}} \frac{1}{2} \sqrt{\frac{1}{2 \pi}}^3 2 \pi \int_0^\infty p^3 \exp{\lpar{-\frac{p^2}{2}}}~ \rmd p \nonumber \\ &=& \rho \sqrt{\frac{T}{\pi}} \sqrt{\frac{1}{m} + \frac{a^2 + b^2}{2I}} \label{eq:avgj} \end{eqnarray}
|
|
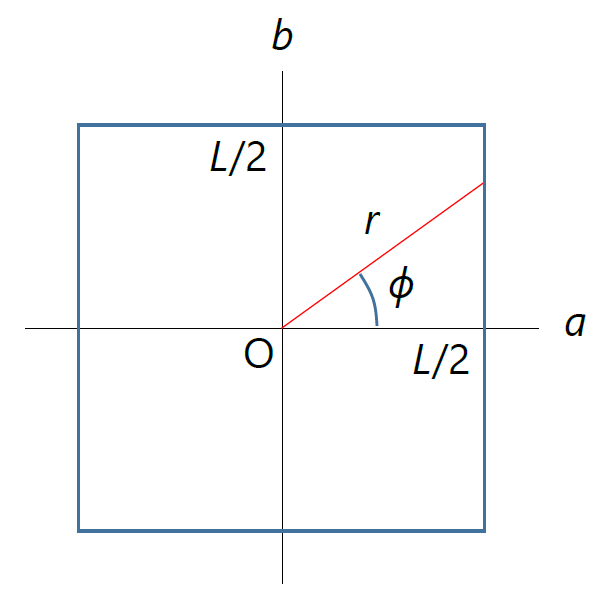
| 図 3X-1. \(a, b\) の積分を極座標系 \(r, \phi\) での積分に変換。 |
さてこの流束を針 A と B のさまざまな配置について足しこんで、 衝突頻度を求めるには次の \(a, b\) についての積分を行う必要があります：
\begin{eqnarray*} Q = \int_{-L/2}^{L/2} \rmd a \int_{-L/2}^{L/2} \rmd b \sqrt{\frac{1}{m} + \frac{a^2 + b^2}{2I}} \label{eq:func1} \end{eqnarray*}
図 3X-1 のような極座標系を使って \(a, b\) についての積分を書き換えると、次式のようになります：
\begin{eqnarray} Q &=& 8 \sqrt{\frac{1}{m}} \int_0^{\pi/4} \rmd \phi \int_{0}^{L/2 \cos \phi} \rmd r ~r \sqrt{1 + \frac{m r^2}{2I}} \nonumber \\ &=& 8 \sqrt{\frac{1}{m}} \frac{2 I}{3m L^2} \int_0^{\pi/4} \rmd \phi \lpar{\sqrt{1 + \frac{m L^2}{8I \cos \phi}}^3 -1} \nonumber \\ &=& \sqrt{\frac{1}{m}} \frac{16 I}{3m L^2} F_{3/2}(m L^2/8I) \label{eq:func2} \end{eqnarray}
ここで \(F_n(x)\) は次式で定義される関数です：
\begin{equation} F_n(x) \equiv \int_{0}^{\pi/4} \rmd \phi \left[ \lpar{1 + \frac{1}{x \cos^2 \phi}}^n -1 \right] \end{equation}
さて針 A と B のなす角を \(\theta\) とすると（\(0 \le \theta \lt \pi\)）、 流束の断面積は \(|\vec{u}_\mrm{A} \x \vec{u}_\mrm{B}| = \sin \theta\) に比例します。 ですからこの配置での衝突頻度 \(Z(\theta)\) は、 表と裏 2 方向からの流束があることに注意して式 \eqref{eq:avgj} と \eqref{eq:func2} を用い、次のように評価できます：
\begin{eqnarray} Z(\theta) &=& \sin \theta \int_{-L/2}^{L/2} \rmd a \int_{-L/2}^{L/2} \rmd b ~2 \avg{j_\mrm{col}}_{a,b} \\ &=& 2 \sin \theta ~\rho \sqrt{\frac{T}{\pi}} Q \\ &=& \sin \theta ~\rho \sqrt{\frac{T}{\pi m}} \frac{32 I}{3m L^2} F_{3/2}(8I/mL^2) \label{eq:colfreq1} \end{eqnarray}
関数 \(F_{3/2}(x)\) はあらわに書き下すと、 ちょっと厄介な格好をしていて、次のようになります：
\begin{equation} F_{3/2}(x) = \frac{1}{2x\sqrt{x}} \lpar{\sqrt{x + 2} + (3x + 1) \ln \frac{\sqrt{x + 2} + 1}{\sqrt{x + 1}}} - \arccos \sqrt{\frac{x}{2(x+2)}} + \frac{\pi}{4} \label{eq:fx3/2} \end{equation}
関数 \(F_{3/2}(x)\) の \(x \to 0\)、\(x \to \infty\) での漸近形は次のようになります：
\begin{equation} F_{3/2}(x) =\left \{ \begin{array} {ll} [(2^{-1/2} + (1/2) \ln(1 + 2^{1/2})] x^{-3/2} & x \to 0 \\ (3/2) x^{-1} & x \to \infty \end{array} \right. \label{eq:fx3/2lim} \end{equation}
最初 \(F_{3/2}(x)\) の積分には手こずって Frenkel たち同様、 数値積分で済ましていたのですが、 たまたま眺めていた岩波の数学公式 I （P. 204）に \(\sqrt{a^2 + b^2 \sin^2 x}/\sin x\) の不定積分が載っていたのが助けになりました。
|
図 3X-2. 慣性モーメントが極めて小さい針 A と B の相対速度ベクトル \(\vec{v}_\mrm{r}\) に垂直な平面に対する射影。 針が高速回転しているので A と B は回転軸の固定された円盤としてふるまい、 回転軸が相対速度ベクトルに対し \(\theta\) 傾いているとすると、 円盤の射影は長径が \(L\)、短径 \(p = L \cos \theta\) の楕円になります。 この楕円が重なる A と B の配置の面積が散乱断面積に相当し、 それを求めるには射影された楕円の周長と面積の平均値が必要になります。 |
慣性モーメントが極めて小さい針 A と B は高速回転しているので、 あたかも円盤のように見なすことができます。 そして両者の散乱断面積は A と B の相対速度ベクトル \(\vec{v}_\mrm{r}\) に垂直な平面に対する円盤の射影、 図 3X-2 のように示すような楕円の重なりの生じる配置の面積の平均になります。 楕円が重なり合う配置の面積の平均 \(\avg{s}\) は、 楕円の周長を \(C\)、面積を \(S\) とすると、 積分幾何の主公式から次式で得られます：
\begin{equation} 2 \pi \avg{s} = C_\mrm{A} C_\mrm{B} + 2\pi (S_\mrm{A} + S_\mrm{B}) \label{eq:funform} \end{equation}
この円盤の射影でできる楕円は、針の回転軸が相対速度ベクトルに対し \(\theta\) 傾いているとすると、 長径が \(L\)、短径 \(p = L \cos \theta\) であり、 回転軸方向についての、楕円の短軸の平均は次のようになります
\begin{equation} \avg{p}_\mrm{proj} = \frac{ \int_0^{\pi/2} (L \cos \theta) \sin \theta ~\rmd \theta}{\int_0^{\pi/2} \sin \theta ~\rmd \theta} = L/2 \label{eq:minaxav} \end{equation}
ですから射影面上での楕円の面積 \(S = (\pi/4) L p\) の平均 \(\avg{S}_\mrm{proj}\) は次のようになります：
\begin{equation} \avg{S}_\mrm{proj} = (\pi/4) L \avg{p}_\mrm{proj}= \frac{\pi}{8} L^2 \label{eq:area_eliav} \end{equation}
楕円の周長の平均は少し厄介です。 楕円の方程式をパラメーター表示で書くと次式のようになるので
\begin{equation} x = (L/2) \cos \phi, ~~ y = (L/2) \cos \theta \sin \phi \end{equation}
楕円の周長 \(C\) は、次のように表すことができます（第２種楕円積分）：
\begin{equation} C = \int_0^{\pi} 2 \sqrt{x_\phi^2 + y_\phi^2} \rmd \phi = 2L \int_0^{\pi/2} \sqrt{\sin^2 \phi + \cos^2 \theta \cos^2 \phi} ~\rmd \phi \label{eq:circ_eli} \end{equation}
針の回転軸の向きについての周長の平均 \(\avg{C}_\mrm{proj}\) は、 楕円の短軸の平均（式 \eqref{eq:minaxav}）同様、次式で与えられます：
\begin{equation} \avg{C}_\mrm{proj} = L \int_0^{\pi/2} \rmd \theta ~\sin \theta \int_0^{\pi/2} 2 \sqrt{\sin^2 \phi + \cos^2\phi \cos^2 \theta} ~\rmd \phi \end{equation}
積分の順序を交換して、\(\theta\) についての積分を行うと次のようになります：
\begin{eqnarray} \avg{C}_\mrm{proj}/L &=& \int_0^{\pi/2} \rmd \phi \cos \phi \int_0^{\pi/2} 2 \sqrt{\tan^2 \phi + \cos^2 \theta} \sin \theta ~\rmd \theta \\ &=& \int_0^{\pi/2} \left[ 1 - \sin \phi \tan \phi \ln \lpar{\tan \frac{\phi}{2}} \right] ~ \rmd \phi \end{eqnarray}
ここで部分積分を行うと次式を得ることができ、
\begin{equation} \avg{C}_\mrm{proj}/L = \int_0^{\pi/2} \rmd \phi \frac{1}{\sin \phi} \ln \lpar{\frac{1 + \tan \frac{\phi}{2}}{1 - \tan \frac{\phi}{2}}} \end{equation}
ここで定石通り \(t = \tan (\phi/2)\) とおいて
\begin{eqnarray} \avg{C}_\mrm{proj}/L &=& \int_0^{1} \frac{1}{t} \ln \frac{1 + t}{1 - t} ~\rmd t \nonumber \\ &=& \int_0^{1} \frac{\ln (1 + t)}{t} ~\rmd t - \int_0^{1} \frac{\ln (1-t)}{t} ~\rmd t \nonumber \\ &=& \frac{\pi^2}{12} + \frac{\pi^2}{6} \nonumber \\ &=& \frac{\pi^2}{4} \label{eq:circ_eliav} \end{eqnarray}
なぜか数学公式集によく載っている定積分に帰着して、 スマートな結果を得ます。 こうして散乱断面積は次式のようになります：
\begin{equation} \avg{s} = (1/32) \pi^3 + (1/4) \pi \label{eq:scat_eli} \end{equation}
式 \eqref{eq:circ_eliav} を導出すること自体は、 あまり悩むことなく力づくでできて、 結果は数値積分でも確認できました。 しかしなぜこうしたスマートな結果になるのか （そもそもスマートかも含め） 未だに謎です。 何かもっと高度な（？）数学的な構造が背景にあると思うんですが・・・