２．古代の知恵 ～～ グッゲンハイム Guggenheim 法のこと

その昔、計算機の利用が一般的でなかったころ、 実験データ \(\{t_i, y_i\}\) を定数項を含む指数関数の式

\begin{equation} y = y_0 + A \rme^{-kt} \label{eq:target} \end{equation}

に当てはめるのに非線形の最小２乗法を適用することは非現実的でした （先の計算例の１回の繰り返し計算で、 何回四則演算することになるかを勘定してみてください。 また有効数字を何ケタとればいいかも考えて見てください）。 そこで次のような解析 （グッゲンハイム Guggenheim 法(1936)）が広く行われました。

1. 時間間隔を等間隔（\(\Delta t\) とします）に取った \(N\) 個の測定データ \(\{i, y_i\}\)（\(i = 0 \ldots N-1\)）を用意します。 そもそもの測定を一定時間間隔で行ってもよいし、 時間間隔が一定でない時は、適宜、内挿なりして等間隔のデータに焼き直します （データの内挿は一般に精度よく行うことができます。 データ点を滑らかな曲線で結んでグラフを描き、図から読み取るといったことも行われました）。
2. データの間の差分 \[ z_i = y_i - y_{i+M} \] を取ります（この間隔 \(M\)（\( \lt N\)）は \(M \Delta t\) が半減期の２倍程度以上になるのが望ましいとされます）。 式 \eqref{eq:target} より、\(z_i\) は次の式に従うはずです： \[ z_i = A \left[1 - \rme^{-kM \Delta t} \right] \rme^{-(k \Delta t) i} = A’ \rme^{-(k \Delta t) i} \]
3. \(\log |z_i|\) を \(i\) に対してプロットすると直線関係 \[ \log |z_i| = \log |A’| - \log \rme (k \Delta t) i = \log |A’| - 0.434 (k \Delta t) i \] が得られ、線形最小２乗法によって勾配から \(k \Delta t\) を評価し、速度定数 \(k\) を得る。

この手法は、\(N\) 個のデータ \(\{y_i\}\) から３つのパラメータ \((y_0, A, k)\) を決める問題を、 \(N - M\) 個のデータ \(\{z_i\}\) から２つのパラメータ \((A’, k)\) を決める問題に焼きなおすことで、 取り扱いやすくしていることに相当します。 また常用対数を扱う上で頻出する log e = 0.434（あるいは ln 10 = 2.303） という数値を敢えてあからさまに出しておきました （われわれ世代以上はたいてい暗記している（た））。

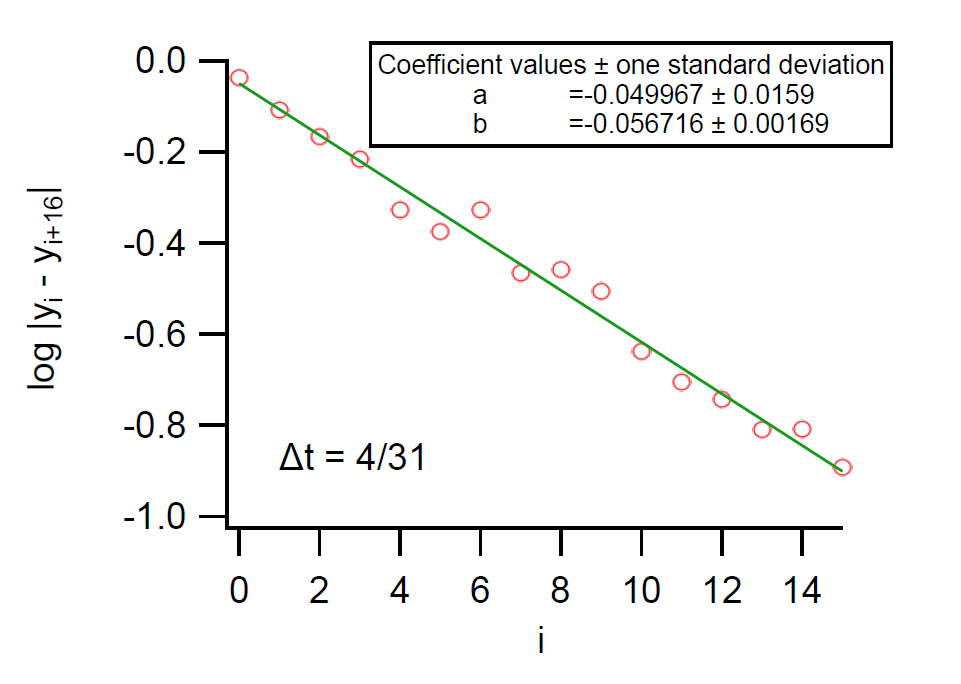
図 2-1. テストデータのグッゲンハイム法による解析

前章のテストデータに、 グッゲンハイム法を適用した結果を図 2-1 に示します。 発生させた \(N\) = 32 個のデータに対し、 \(M\) = 16 にとっています （\(\Delta t\) = 4/31 = 0.1290...）。 予期通りに直線関係が得られ、 Igor を用いて線形の式 a + bx に当てはめた結果、 勾配は 0.0567 ± 0.0017 になります。 ここから速度定数 k を求めると次の通りです：

k = 0.0567 / (log e × (4/31)) = 1.012 (± 0.030)

非線形の最小２乗法では 0.993 ± 0.036 でしたから（0 ≤ x < 4 の当てはめの場合（\(N\) = 32）） 妥当な結果と言ってよいでしょう。

パーソナルコンピュータの普及とともに、非線形の方程式を数値的に解くことが容易になり、 Igor などの市販のソフトには、実験データを非線型方程式にあてはめる機能が標準で組み込まれ、 こうした取り扱いは今や昭和の老人の昔話となりました。 けれども元のデータセットに何らかの変換を行って、 事態の見通しをよくするというアプローチには、 学ぶべきところがないとまでは言えないのではないのではなかろうかと思ったりもするのです・・・

上のグッゲンハイム法の扱いで、自然対数ではなく常用対数を使用しているのは、 ある種、ぼくのノスタルジーのなせるところです。 関数電卓の使用もままならなかった頃、 対数を取る、対数を引くという作業は、数表との格闘でもありました。 右図は、ぼくが愛用していた培風館の新数学シーズで出ていた数表の一部です （２回生から関数電卓のおかげで解放されました！ 計算尺で有名なヘンミの出していた関数電卓でしたが、本当にお世話になりました）。 今ではこうした対数表の見方も、 常用対数を使った計算法も耳遠いものになっているでしょう。

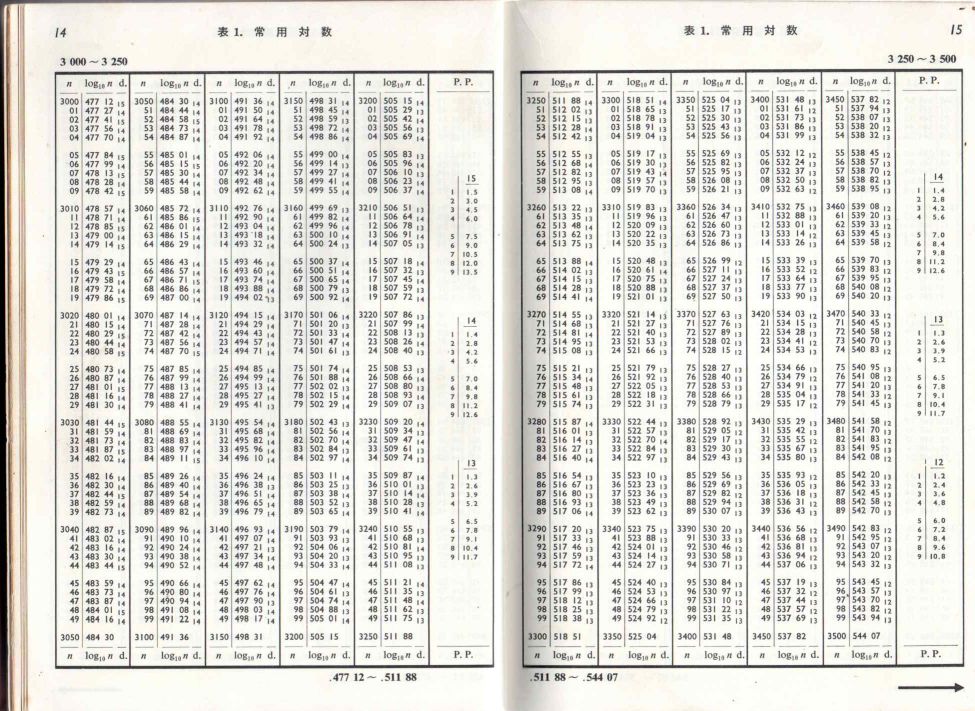
　10年近く前だったか TA の諸君に、 塩化ブチルの加水分解反応についての論文を紹介したところ、 論文中の「2_.464」 というのが話題になりました。 これが、0.0291（真数）の常用対数であること、 0.464 が仮数で（= log 2.91）、2 の上に – が付いているのは、これが指標で 10^-2 の意味で、 log 0.0291 = -1.536 とせずに、 log 0.0291 = -2 + 0.464 とするのが常用対数を扱う上での常識だ（だった）と説明しながら、 つくづく時代の流れを感じさせられるとともに、 何か大事なものが失われたのではないかとも思いました。 昔はこうした常用対数との対話（？）の中で、 おのずと有効数字（0.0291 = 2.91 × 10^-2）についても体感するところがありました。 今の時代もう一度、実習や演習のカリキュラムの中で取り上げてみるのも有意義かなと思う次第です。

表紙のページへ