2025.11
吉村洋介
指数関数への当てはめをめぐって
0.最小2乗法の非線形関数への適用
データのセット \(\{t_i ,y_i\} ~~ (i = 1, \ldots, N)\) を、
ある関数 \(f(\vec{p}; t)\) に当てはめることを考えます。
測定データ \(\{y_i\}\) はそれぞれ独立の測定値で、
その不確かさの分散 \(\sigma^2\) は同一であるとします。
また \(\vec{p}\)(= \((p_1, p_2, \ldots, p_M)\)) は関数を特徴づけるパラメーターで、
\(\vec{p}\) の \(M\) 個の成分をデータセットから、
もっともらしく決定することになります。
最小2乗法では、
測定値 \(y_i\) の関数 \(f\) との差、残差 \(R_i\) について、
次の残差2乗和 \(S(\vec{p})\) を最小にするようにパラメーター \(\vec{p}\) を決めます:
\begin{equation}
S(\vec{p}) = \sum_i {R_i^2}
= \sum_i {[y_i - f(\vec{p}; t_i)]^2}
\label{eq:sqrres}
\end{equation}
関数 \(f(\vec{p}; t)\) がパラメーター \(\vec{p}\) について線形の関数であれば、
これは線形代数で習う2次形式の問題になっていて、
形の上では簡単に解ける話ですが、指数関数を含むような非線形の関数になってくると厄介です。
ここでは Igor などの解析用のソフトを使用する上で大事だと思われるポイントについて、
ざっくりと触れておきます。
0-1.最小2乗法による非線形方程式への当てはめ:1 パラメーターの場合
もっとも単純な \(M\) = 1 のケース、
1 個のパラメーター \(a\)(= \(p_1\))で記述できる場合について考えましょう。
式 \eqref{eq:sqrres} の残差2乗和 \(S(a)\) が最小になる場合には、
\(a\) についての微分が 0 になっていますから、
次の方程式を解けばいいわけです:
\begin{equation}
\frac{\partial S(a)}{\partial a} = \sum_i {-2 [y_i - f(a; t_i)] f_a(a; t_i)} = 0
\label{eq:normeqx}
\end{equation}
ここで \(f_a(a; t_i)\) は \(f(a; t_i)\) の \(a\) についての偏微分係数です。
この方程式は非線形の方程式で、一筋縄ではいきません。
そもそも解が存在しないこともありますが、
まずは解があるという前提で話を進めます。
さまざまな解法がありますが、ニュートン(-ラフソン)法を利用するのが普通です。
式 \eqref{eq:normeqx} を解くのに、
簡単のため次の関数 \(X(a)\) を考え
\begin{equation}
X(a) = \sum_i {R_i f_a(a; t_i)} =
\sum_i {[y_i - f(a; t_i)] f_a(a; t_i)}
\label{eq:normeqxx}
\end{equation}
次の方程式(正規方程式)で考えます。
\begin{equation}
X(\alpha) = 0
\label{eq:normeq0}
\end{equation}
式 \eqref{eq:normeqxx} を \(a_n\)(\(n \ge 0\))の周りで展開し
\begin{equation}
X(a_{n+1}) \approx X(a_n) + X'(a_n) (a_{n+1} - a_n) = 0
\label{eq:normeqy}
\end{equation}
となるように \(a_{n+1}\) を決め、初期値
\(a_0\) を適当に与えて(Igor Pro で ”Initial Guess” とされているもの)、
次の漸化式で数列 \(\{a_n\}\) を作ります。
\begin{equation}
a_{n+1} = a_n - \frac{X(a_n)}{X'(a_n)} =a_n + \Delta a_n
\label{eq:normeqyy}
\end{equation}
ここで \(X'(a)\) は \(X(a)\) の \(a\) についての微係数です。
この数列が \(\alpha\) に収束すれば、\(X(\alpha)\) = 0 が成り立っているわけで、
収束値 \(\alpha\) が式 \eqref{eq:normeqx} の解、
求める残差2乗和を最小にする \(a\) の値になります
(正しくは極小で、最小とは限りませんがそれはここでは置いておきます)。
もしデータセットに対する当てはめがうまく行っておれば、
\(R_i\) は十分小さいと見なせるので、次式のように近似できます(ガウス-ニュートン法):
\begin{equation}
X'(a) = \sum_i {R'_i f_{a}(a; t_i) + R_i f_{aa}(a; t_i)} \approx
\sum_i {- [f_{a}(a; t_i)]^2}
\label{eq:normeqyy0}
\end{equation}
実験
式ばかりではイメージがつかめない人がいるかもしれないので「実験」してみましょう。
関数として
\[
f(a; t) = a \rme^{-at}
\]
を考え、
この関数を次のようなデータに当てはめます:
表 0-1. 当てはめる実験データ
| \(t\) | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
| \(y\) | 1.038 | 0.788 | 0.715 | 0.536 | 0.431 | 0.383 | 0.338 | 0.265 | 0.170 | 0.208 | 0.183 |
表 0-1 のデータについて、初期値に \(a_0\) = 1.2 をとり、
数列 \(\{a_n\}\) を漸化式 \eqref{eq:normeqyy}
をガウス-ニュートン法で計算した結果を表 0-1a に、
\(X'(a)\) の \(f(a; t)\) の 2 階微分の項も計算したニュートン法の結果を
表 0-1b に示します。
表 0-1a. ガウス-ニュートン法
| \(n\) | \(a_n\) | \(S(a)\) | \(X(a)\) | \(X'(a)\) | \(\Delta a_n\) |
| 0 | 1.20000 | 0.06988 | -0.30115 | -1.56253 | -0.19273 |
| 1 | 1.00727 | 0.01173 | 0.00662 | -1.70446 | 0.00388 |
| 2 | 1.01115 | 0.01171 | -0.00003 | -1.70108 | -0.00002 |
| 3 | 1.01113 | 0.01171 | 0.00000 | -1.70109 | 0.00000 |
表 0-1b. ニュートン法
| \(n\) | \(a_n\) | \(S(a)\) | \(X(a)\) | \(X'(a)\) | \(\Delta a_n\) |
| 0 | 1.20000 | 0.06988 | -0.30115 | -1.49133 | -0.20194 |
| 1 | 0.99806 | 0.01200 | 0.02246 | -1.72833 | 0.01300 |
| 2 | 1.01106 | 0.01171 | 0.00012 | -1.71020 | 0.00007 |
| 3 | 1.01113 | 0.01171 | 0.00000 | -1.71010 | 0.00000 |
|
|
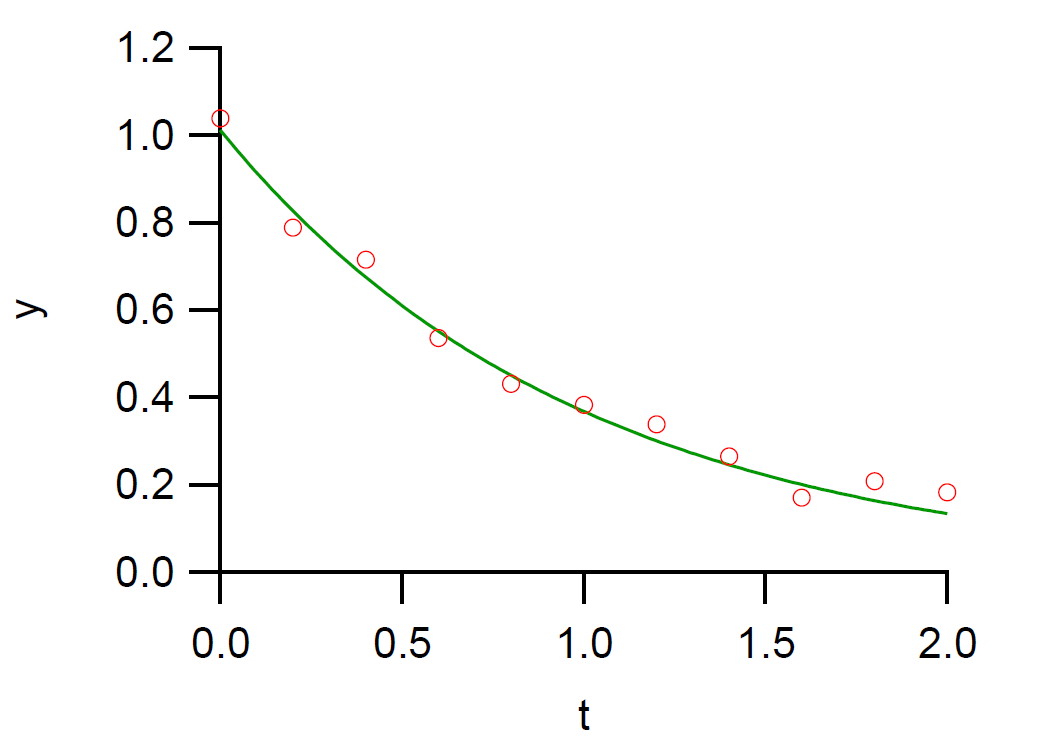
図 0-1. 非線形最小2乗法により、データを関数 \(a \rme^{-at}\) に当てはめた結果。
\(\alpha\) = 1.01113。
|
ガウス-ニュートン法も(元祖)ニュートン法も
数列は急速に収束し、両者ともに収束値 \(\alpha\) として 1.01113 を得ます。
収束に必要な数列の長さにも違いはありません。
式 \eqref{eq:normeqyy0} で 2 階微分の項を無視したガウス-ニュートン法で、
式 \eqref{eq:normeqx} の解を得るのに十分であることが分かります。
また式 \eqref{eq:normeqyy0} からも明らかに \(X'(\alpha) \lt 0\) で、
これは得られる極値が極大ではなく極小であることを保証してくれます
(\(\partial S(a)/\partial a = -2X(a)\) に注意)。
表 0-1 のデータ点と非線形最小2乗法で当てはめた関数 \(a \rme^{-at}\) を、
図 0-1 に示しました。
想定した関数形がデータを説明する上でもっともらしいものであり、
データが 1 つのパラメーター \(\alpha\) で特徴づけられるようになったといえるかもしれません。
そこにどのような意味を見出すかは、また別のはなしですが・・・
0-2.パラメーターの信頼区間:1 パラメーターの場合
先ほどの扱いではデータ \(\{y_i\}\) に対してパラメーター \(a\) のもっともらしい値 \(\alpha\) を定めることを考えました
(残差2乗和 \(S(a)\) が \(a = \alpha\) で最小になる)。
今度はデータ \(\{y_i\}\) が変動した時に、
もっともらしく決めたパラメーター \(\alpha\) がどれくらい変動するかを考えます。
大ざっぱに言えば線形の最小2乗法で見るような
\begin{equation}
\var{a^2} = K(\alpha; \{t_i\}) \var{y^2}
\label{eq:perr0}
\end{equation}
という関係を想定して、データの分散に対するパラメーターの分散の比例係数 \(K(\alpha; \{t_i\})\)
を決める問題です。
データ \(y_i\) が変動して最適のパラメーター値 \(\alpha\) が \(\delta a\) 変化したとした時、
方程式 \eqref{eq:normeq0} から次の関係がなりたっています:
\begin{equation}
X(\alpha + \delta a) = X(\alpha) + X'(\alpha) \delta a
\approx \sum_i {[y_i - f(\alpha; t_i)] f_a(\alpha; t_i)} + \sum_i {-[f_a (\alpha; t_i)]^2} \delta a
= 0
\label{eq:perr1}
\end{equation}
この関係式で \(y_i\) が揺らいだ時のパラメーター \(\alpha\) の揺らぎを、
それぞれの分散で評価します。
ここで次の関係に注意します:
\begin{equation}
\var{\{[y_i - f(\alpha; t_i)] f_a(\alpha; t_i)\}^2} = \var{[y_i f_a(\alpha; t_i)]^2} = [f_a(\alpha; t_i)]^2 \var{y_i ^2}
= [f_a(\alpha; t_i)]^2 \sigma^2
\label{eq:perr2}
\end{equation}
つまり元のデータ \(\{y_i\}\) の揺らぎが分散 \(\sigma^2\) を持っていたとすると、
そこから決まる最ももっともらしいパラメーター \(\alpha\) には次式で表される分散を考慮する必要があることになります:
\begin{equation}
\var{\alpha^2} = \var{(\delta \alpha)^2} = \frac{1}{\sum_i {[f_a (\alpha; t_i)]^2}} \sigma^2
\label{eq:perr3}
\end{equation}
この関係を確認するには、当てはめの関数として \(f(a; t_i) = a\)
をとり最小2乗法を適用することを考えていただければいいかもしれません。
この場合、最小2乗法からは \(\alpha = \sum_i y_i/N\) ですし、
その分散は \(\var{\alpha^2} = \sigma^2/N\) ですよね。
また分散が分かっていない時には、残差2乗和から分散が評価できます
(不偏推定を取らず単に \(N\) で割る流儀もある):
\begin{equation}
\sigma^2 = \avg{S(\alpha)/(N-1)}
\label{eq:varsamp}
\end{equation}
0-3.多パラメーターの場合のスケッチ
多くのパラメーターを含む関数、
たとえば今回扱う3 パラメーターを含む次のような関数への非線形最小2乗法の適用は、
線形の最小2乗法の手続きに、
前節までに述べた非線形方程式の扱いを組み合わせたものだといってよいでしょう。
\begin{equation}
f(\vec{p}; t) = p_1 + p_2 \rme^{-p_3 t}
\label{eq:expfunc}
\end{equation}
ただし 1 パラメーターの場合には単に逆数を取ればよかったところが、
ベクトルを扱う関係で逆行列を取ったりしないといけなくなります。
ここではどのような取り扱いになるのかの、
簡単なスケッチに止めます。
残差2乗和の極値を求めるための方程式(正規方程式)は、
次の連立方程式になります:
\begin{equation}
\vec{X}(\vec{p}) = 0
\label{eq:xnormeq0}
\end{equation}
ここで \(\vec{X}(\vec{p})\) の \(n\) 番目の成分は次式で与えられます:
\begin{equation}
X_n(\vec{p}) = \sum_i {R_i f_n(\vec{p}; t_i)}
\label{eq:xnormeq0a}
\end{equation}
この連立方程式を解くのに、適当なベクトル \(\vec{p}_0\) を与えて、
次の漸化式でベクトル列 \(\vec{p}_{n}\) を作り、
それが収束したところ \(\vec{\pi}\) が、正規方程式 \eqref{eq:xnormeq0} の解、
残差2乗和を極小にする解となります。
\begin{equation}
\vec{p}_{n+1} = \vec{p}_n - X'(\vec{p}_n)^{-1} X(\vec{p}_n) =\vec{p}_n + \Delta \vec{p}_n
\label{eq:xnormeqyy}
\end{equation}
ここで \(X'(\vec{p})\) は、その \((k, l)\) 成分が次式で与えられる \(M \x M\) の行列です
(ガウス-ニュートン法を適用しています):
\begin{equation}
X'(\vec{p})_{k, l} = -\sum_i { f_{k}(\vec{p}; t_i) f_{l}(\vec{p}; t_i)}
\label{eq:hessian0}
\end{equation}
ここで \(f_{k}(\vec{p}; t_i)\) は、関数 \(f(\vec{p}; t_i)\) の \(p_k\) による偏微分を示します。
正規方程式 \eqref{eq:xnormeq0} の解、\(\vec{\pi}\) の信頼区間については、
パラメーターが必ずしも互いに独立でないことに注意します。
得られたパラメーターの共分散行列 \(\var{{}^t \vec{\pi} \vec{\pi}}\)
は次式で与えられます:
\begin{equation}
\var{{}^t \vec{\pi} \vec{\pi}} = X'(\vec{\pi})^{-1} \sigma^2
\label{eq:xcovar}
\end{equation}
実験 2
実験 1 の表 0-1 のデータを関数
\[
f(a, b; t) = b \rme^{-at}
\]
を考え、先の実験 1 の表 0-1 のデータに当てはめてみます。
\(\vec{p} = (a, b)\) とし、初期値に \(\vec{p}_0\) = (1.2, 1.2) をとり、
漸化式 \eqref{eq:xnormeqyy} を計算した結果を表 0-2 に示します。
表 0-2. 2 パラメーターの場合のガウス-ニュートン法の計算例
| \(n\) | \(a\) | \(b\) | \(S(\vec{p})\) | \(\vec{X}_1\) | \(\vec{X}_2\) |
| 0 | 1.20000 | 1.20000 | 0.06988 | -0.00593 | -0.29523 |
| 1 | 0.98601 | 1.00641 | 0.01069 | -0.01597 | 0.02070 |
| 2 | 0.97227 | 1.00793 | 0.01043 | -0.00013 | -0.00012 |
| 3 | 0.97196 | 1.00777 | 0.01043 | -0.00001 | 0.00000 |
| 4 | 0.97195 | 1.00776 | 0.01043 | 0.00000 | 0.00000 |
2 パラメーターの場合に拡張しても、
無事収束してくれています。
ただし最初のところを見ると、\(\vec{X}(1)_1\) で小さくなりすぎていて(-0.00593 → -0.01597)、
足取りが少し乱れています。
パラメーターが増えると、
こうしたことが頻発するようになって、
いろんな工夫が必要になっていきます。
パラメーターの信頼区間についての計算も示しておきましょう。
まず測定データのばらつき具合、分散 \(\sigma^2\) があらかじめ分かっていない場合、
最小値として得られた残差2乗和 \(S_\mrm{min}\) から評価し、
不偏推定になるように \(N - M\) で割るのが普通です
(ざっくり \(N\) で割る立場もある)。
\(\sigma^2 \approx S_\mrm{min}/(10-2)\) = 0.01043/8 = 0.00130
\(\sigma\) = 0.0361
|
|
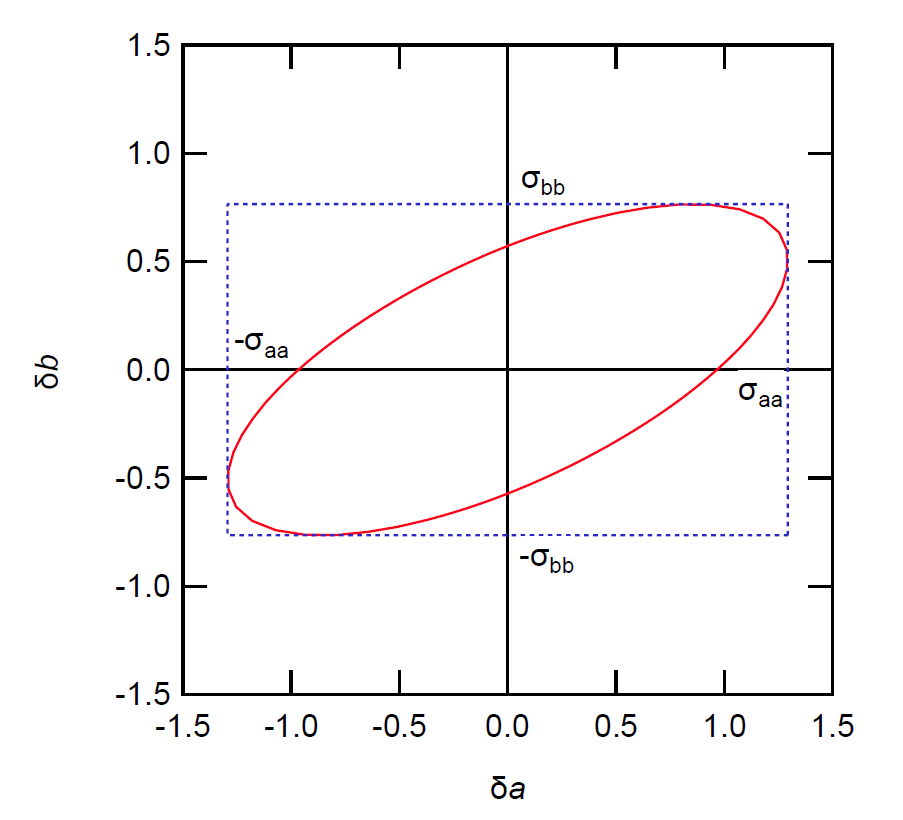
図 0-2. 測定データが分散 \(\sigma^2\) 程度揺らいだ時、
最小 2 乗法で決めたパラメーター \((a, b)\) の変動 \((\delta a, \delta b)\) の範囲。
|
パラメーター \((a, b)\) の共分散行列の計算結果は、表 0-3 のようになります。
表 0-3. 2 パラメーター \((a, b)\) の共分散行列(\(\sigma^2\) = 1 とする )
| a | b |
| a | 1.6735 | 0.6576 |
| b | 0.6576 | 0.5850 |
表 0-3 で \(\sigma_{ab}^2 = \var{ab} \ne 0\) であることからも明らかに、
最小2乗法で決めたパラメーター \(a\) と \(b\) は、
統計的に独立ではありません。
仮に元のデータが分散 \(\sigma^2\) だけ揺らいだ時に、
そこから決定されるパラメーターが変化するであろう範囲を、
図 0-2 に描いてみました。
パラメーターの信頼区間(”誤差”)を問題にする時に、
こうしたパラメーターの共分散も念頭においておく必要がありますが、
次のように自己分散(\(\var{a^2}\)、\(\var{b^2}\))に基づく解析結果を出すに止めることが多いです。
\(a\) = 0.97195 ± 1.294 \(\sigma\) = 0.97195 ± 0.047
\(b\) = 1.00776 ± 0.765 \(\sigma\) = 1.00387 ± 0.028
± 以下は標準偏差。
次のページへ
表紙のページへ

