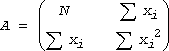付録Ａ. なぜ s₀²の計算において N - m で割るのか？

(25)式は次のようにして導ける。

v = y - X a (A1)

dy = y - y₀ (A2)

da = a - a₀ (A3)

とおく。ここで y₀、a₀ は、それぞれ真の y、a の値である。 こうおくと、y₀ = Xa₀ のはずだから

v = dy - X da　　(A4)

と書ける。

さて問題は、^Tvv = |v|²の期待値を y の分散 s₀²でどのように表現できるかにある。まず ^Tvv をあからさまに書いてみると次のようになる。

Tvv = (d^Ty - d^Ta ^TX) v = d^Ty v - d^Ta ^TX v　　(A5)

(A5)式の右辺第２項は、

d^Ta ^TX (y - X a) = d^Ta (^TX y - ^TX X a) (A6)

であり、正規方程式(23)から0に等しい。したがって

^Tv v = d^Ty v = d^Ty dy - d^Ty X da　　(A7)

という式を得る。この期待値をとると、第１項は

E(d^Ty dy) = E[S (dy_i)² ] = N s₀²　　(A8)

第２項は少しやっかいだが、(24)式から

E[d^Ty X da] = E[d^Ty X (^TXX)^{-1 T}X dy] (A9)

となり、E(dy_idy_j)=0 (i ≠j)に注意して

E[d^Ty X da] = Tr [X (^TXX)^{-1 T}X ] s₀²　　(A10)

巡回置換についてトレースは不変だから、

E[d^Ty X da] = Tr [X (^TXX)^{-1 T}X ] s₀²

= Tr [(^TXX)^{-1 T}XX] s₀²

= Tr[I_m ] s₀²

= m s₀²　　(A11)

をえる。ここで I_m は m×m の単位行列。(A6)および(A9)式から結局

E(^Tvv) = (N - m) s₀²　　(A12)

となり、これは s₀² が (25)式で（あるいは(15)式で）推定される事の根拠となる。

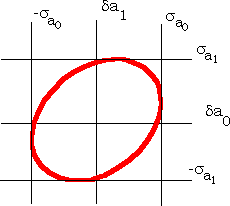
(13)、(14)式の a₀ および a₁ の偏差の推定は、da₀ と da₁ が独立でないので注意が必要である。

(11)式の dS(a) を次のように書き直す。

s₀² dS(a) = d^Ta A da 　　（B1)

ここで A は

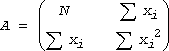　　(B2)

A は正定値だから、dS(a) を固定した時、da₀ と da₁ はダ円を描く。先の s_a0、s_a1は、 dS(a) = 1 とおいた時の da₀ と da₁ それぞれの最大値を求めた事になっている。なお(B2)式から明らかに、Σx_i = 0に選んだ時、da₀ と da₁ はそれぞれ独立になる。