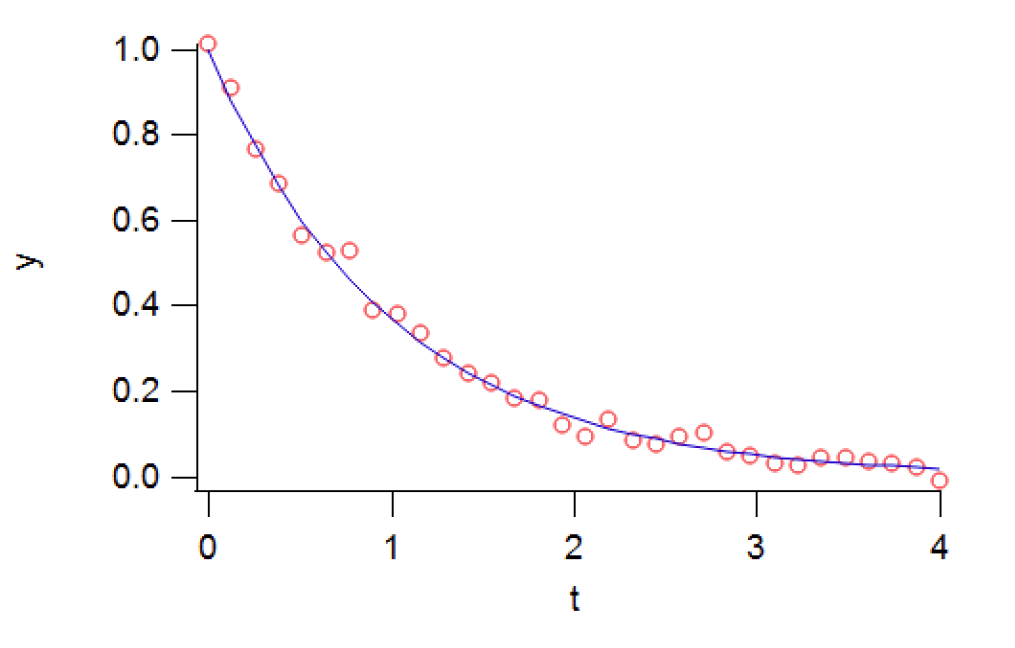
| 図 1-1. 典型的なテストデータ。N = 32, δ t = 4/31 = 0.129...。 |
学生実験の実習の中で、 Igorで時刻 0 ≤ \(t\) ≤ 4 の範囲で 32 点からなるテストデータを発生させ、 最小2乗法で当てはめた結果を調べてもらいます(gnoise(0.02)は標準偏差0.02の正規乱数を発生させる関数):
y = exp(-t) + gnoise(0.02)

| 図 1-1. 典型的なテストデータ。N = 32, δ t = 4/31 = 0.129...。 |
こうしておいて、Igorで exp_XOffset 関数
\begin{equation} y = y_0 + A \exp{\left[-\frac{x-x_0}{\tau}\right]} \label{eq:exp_XOffset} \end{equation}
ここではオフセット \(x_0\) = 0 とします。 Igor で用意されている exp 関数を使ってもよいのですが、 使用は推奨されていません。
への当てはめを行い
を検討してもらいます。
最初の課題 a については、典型的には次のような結果になると思います:
| 当てはめ範囲 | y0 | ± y0 | A | ± A | τ | ± τ |
| 0 ≤ x < 1 | 0.153 | 0.203 | 0.868 | 0.189 | 0.766 | 0.305 |
| 0 ≤ x < 2 | -0.018 | 0.048 | 1.025 | 0.042 | 1.041 | 0.109 |
| 0 ≤ x < 3 | 0.000 | 0.017 | 1.011 | 0.018 | 0.999 | 0.053 |
| 0 ≤ x < 4 | -0.003 | 0.009 | 1.013 | 0.014 | 1.007 | 0.036 |
ここで注目していただきたいのは、y0、A、τ それぞれの値もともかく、推定の標準偏差± の大きさです。 測定のばらつきが 2 %程度(gnoise(0.02))なわけですが(典型的な実験の測定精度と考えてよい)、 これで速度定数を 10 %程度の精度で決めようと思うと実験は 2/k = 2 τ ≈ 3τ1/2(半減期の3倍)くらいまではやらないといけないというわけです。 いろいろ参考書を見てもらうと「3半減期くらい測定する必要がある」と書いてあったりするのは、こうした事情があります。 3回生の実験で出会う塩化ブチルの加水分解反応では、 例えば 30 °Cで τ1/2 が1000 sぐらいなものですから 1 時間ぐらいも測ればいいというわけです。
さて (y0, A, τ) という3つのパラメーターがあるわけですが、 課題 b では y0 の値を固定して(y0 = 0)当てはめを行ってもらいます (Igor の curve fitting のオプションの coefficients で、 y0 の欄の Hold? をチェックして、Initial Guess を 0 にする)。 典型的には次表のような結果が得られ、 測定時間がもっと短くても、 10 %程度の精度が得られることも確かめていただけると思います
| 当てはめ範囲 | y0 | ± y0 | A | ± A | τ | ± τ |
| 0 ≤ x < 1 | 0 | 0 | 1.012 | 0.025 | 0.995 | 0.063 |
| 0 ≤ x < 2 | 0 | 0 | 1.011 | 0.016 | 1.003 | 0.028 |
| 0 ≤ x < 3 | 0 | 0 | 1.012 | 0.015 | 1.000 | 0.023 |
| 0 ≤ x < 4 | 0 | 0 | 1.012 | 0.013 | 0.999 | 0.020 |
このことは、\(y_0\) が分かっておれば速度定数を決めるのに
\begin{equation} \ln |y - y_0| = \ln A - k t \label{eq:lneq} \end{equation}
といった関係から、簡易な線形最小2乗法が使えることからも察しが付くことでしょう (この場合データのばらつきが等分散ではありませんが・・・)。 ですから遅い反応の場合には、例えば加熱して反応を促進する、 翌日に測定するなどして \(t\) → ∞ における \(y\) の値(\(y_0\) 相当)を得るといったことも考えられます。 けれども他の反応が起きたり、装置の安定性の問題などがあって、実際に \(y_0\) を評価するのは難しいことが多いのです。
なお実験課題では32点のデータへの当てはめを扱いますが、これを例えば128点、512点と増やしていくと、 データ点の数を4倍にするごとにパラメータの標準偏差が約半分になることが分かると思います。 1秒間隔でデータを取れば4秒間隔でデータを取るより2倍精度が向上する・・・。 こうなれば話がうまいのですが、 実際の測定では今回のテストデータで発生させているような白色ノイズではありません。 またそもそもの温度などの実験条件の再現性の問題があって、 得られた速度定数の自体のゆらぎが問題となります。