「紙の上のはなし」ばかりでは退屈でしょうから、 実際の反応に即した解析の例を紹介しましょう。
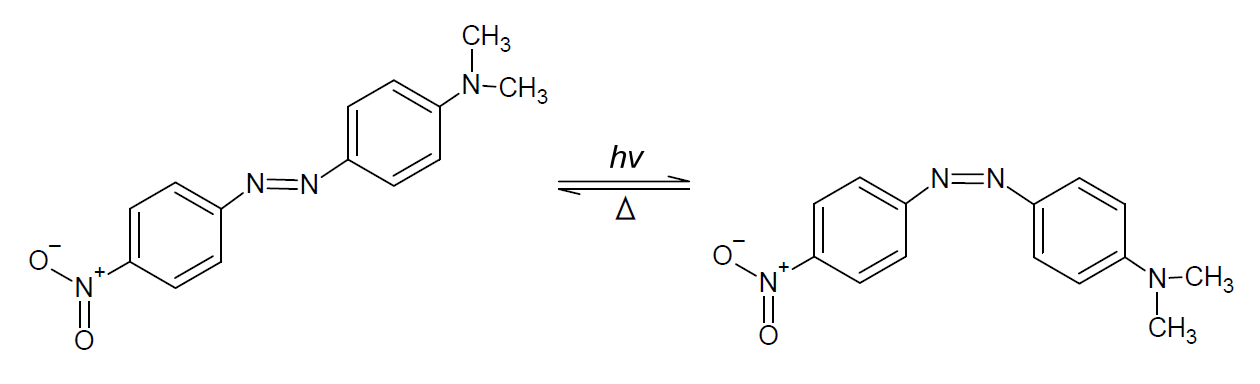
アゾベンゼンは通常 E 体(トランス体)が安定ですが、 光を吸収して一部異性化して Z 体(シス体)となり、 光照射を止めると、熱異性化して再び E 体に戻ります。 無置換のアゾベンゼンの熱異性化速度は遅く、 室温で Z 体を安定に取り出すことも可能ですが、 置換体の中には室温で熱異性化速度を学生実験で実施可能な時間スケールで追跡可能なものもあります (速度定数が 10-4 s-1 ~ 10-2 s-1 程度。 水中のメチルオレンジのように ps オーダー以下で完結してしまうものもある)。 ここでは図 3-1 に示す、4-ニトロ-4'-(ジメチルアミノ)アゾベンゼン(以下 NDMAB と略称します) の E-Z 異性化反応を取り上げます。

| 図 3-1. 4-ニトロ-4'-(ジメチルアミノ)アゾベンゼン(NDMAB)の E-Z 異性化反応。 |
|
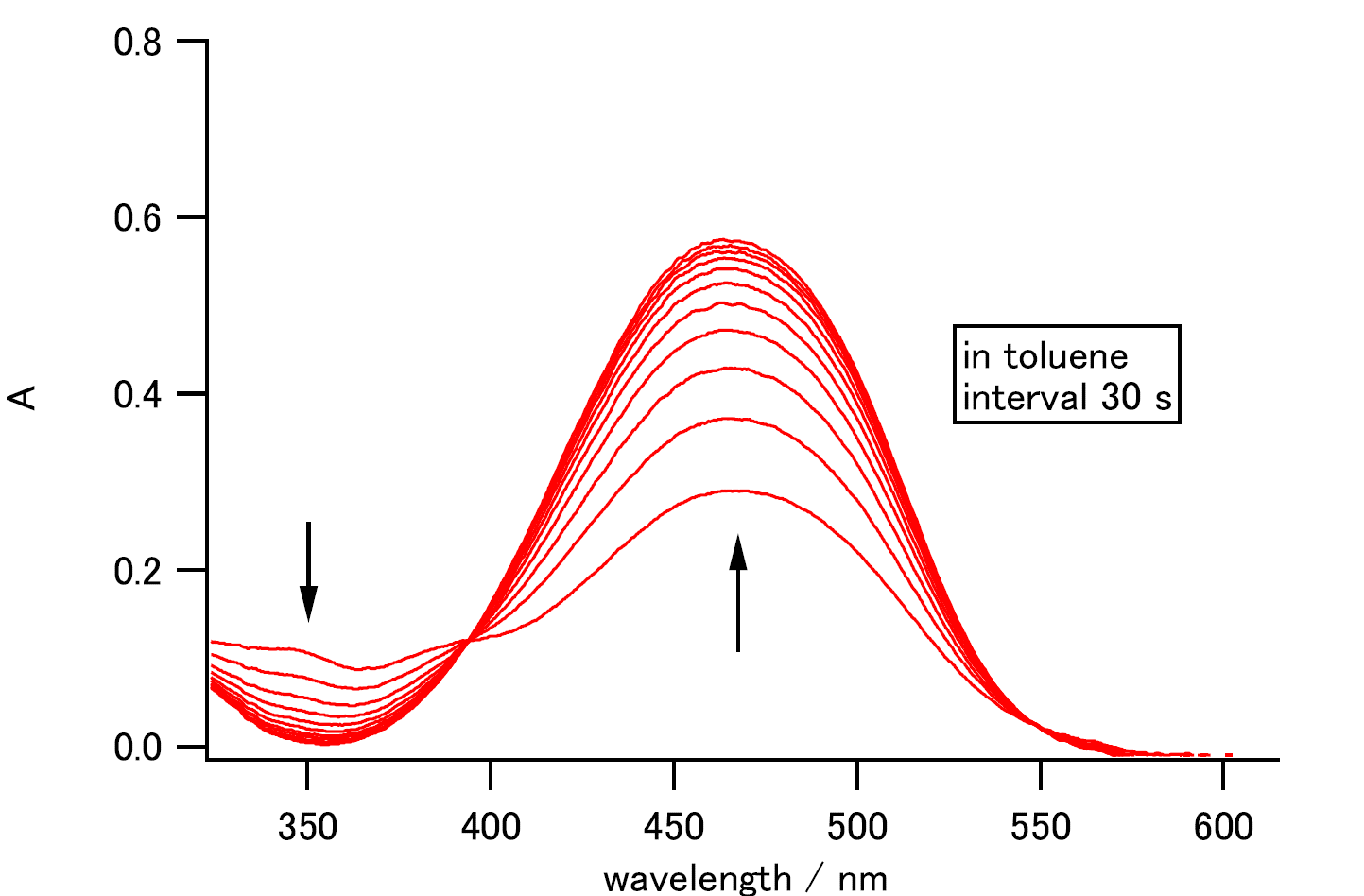
| 図 3-2 4-ニトロ-4'-(ジメチルアミノ)アゾベンゼン(NDMAB)の熱異性化にともなう吸収スペクトルの時間変化。 スペクトルの時間間隔は 30 s。 室温でトルエン中、濃度 2 × 10-5 mol/L。 |
図 3-2 には室温で NDMAB のトルエン溶液に、 青の LED ライト(極大波長 460 nm)を照射後の光吸収スペクトルの時間変化を示しました (小型分光光度計 CHEMUSB 4 を用いて測定)。
光照射の終了後、一部 Z 体になったアゾベンゼンは、 熱的により安定な E 体に変化し、 Z 体と E 体の違いに応じた吸収スペクトルの変化が起きます。 図 3-2 に見るように 470 nm 付近の吸収が増加するとともに 350 nm 付近の吸収が減少し、 394 nm に等吸収点が現れます。
さて E 体が減った分だけ Z 体が生成するわけですから、 平衡状態の濃度からの変化量 \(z\) について次の関係が成り立ちます:
\begin{equation} z = -([\mrm{E}] - [\mrm{E}]_\mrm{e}) = [\mrm{Z}] - [\mrm{Z}]_\mrm{e} \label{eq:advance} \end{equation}
ここで \([\mrm{E}]\) は E 体の、\([\mrm{Z}]\) は Z 体の濃度を示し、 下付きの \(\mrm{e}\) は平衡状態での量であることを示します。 \(z\) を用いると吸光度 \(A\) はベールの法則から、吸光係数 \(\epsilon\) を用いて 次式のように表されます(光路長は 1 とします):
\begin{equation} A = \epsilon(\mrm{E}) [\mrm{E}] + \epsilon( \mrm{Z})[\mrm{Z}] = \epsilon( \mrm{E}) [\mrm{E}]_\mrm{e} + \epsilon( \mrm{Z})[\mrm{Z}]_\mrm{e} + (-\epsilon(\mrm{E}) + \epsilon(\mrm{Z})) z = A_\mrm{e} + \Delta \epsilon z \label{eq:absorbance} \end{equation}
ここで \(\Delta \epsilon\) は E 体と Z 体の吸光係数の差(\(-\epsilon(\mrm{E}) + \epsilon(\mrm{Z})\))です。 E 体と Z 体の吸光係数の等しくなる波長では、 吸光度は平衡状態の吸光度に等しく時間変化しません (等吸収点 isosbestic point)。
1 次反応の速度則は \(z\) を用いて次のように書けます:
\begin{equation} \frac{\rmd z}{\rmd t} = -kz \label{eq:rateeqx} \end{equation}
ここで \(k\) は速度定数です。 これを積分すると次式になります:
\begin{equation} z = z_0 \rme^{-kt} \label{eq:advanceint} \end{equation}
よく行われる速度論の解析では、この速度定数 \(k\) は、 正反応と逆反応の速度定数の和(\(k_+ + k_-\))とされます。
ここで下付きの 0 は時刻 \(t\) = 0 での量であることを示します。 ですから吸光度の変化を、 \(\Delta \epsilon \ne 0\) である波長で観測し、 それを指数関数に当てはめてやれば、速度定数が得られることになります。
\begin{equation} A = A_\mrm{e} + \Delta \epsilon z_0 \rme^{-kt} \label{eq:abschange} \end{equation}
|
|
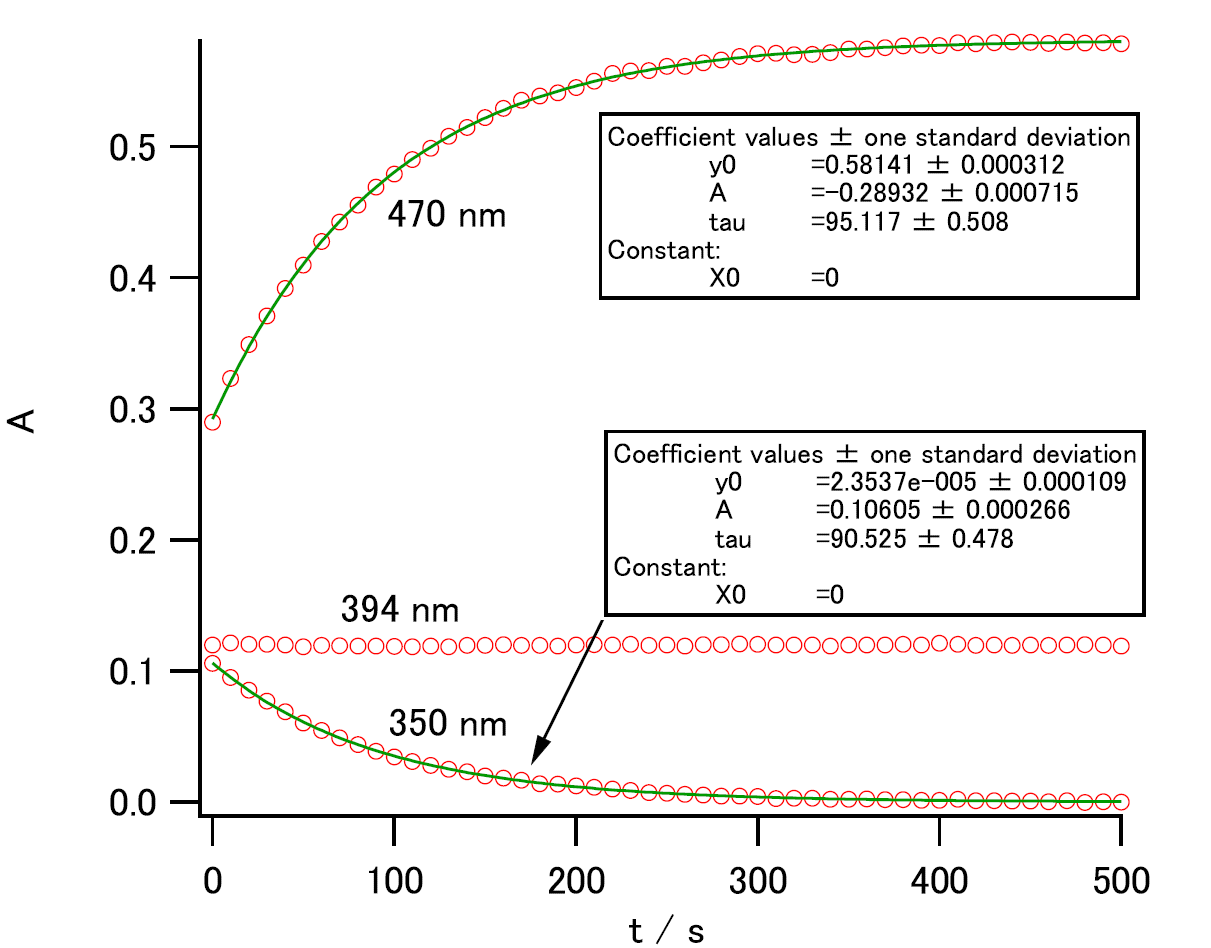
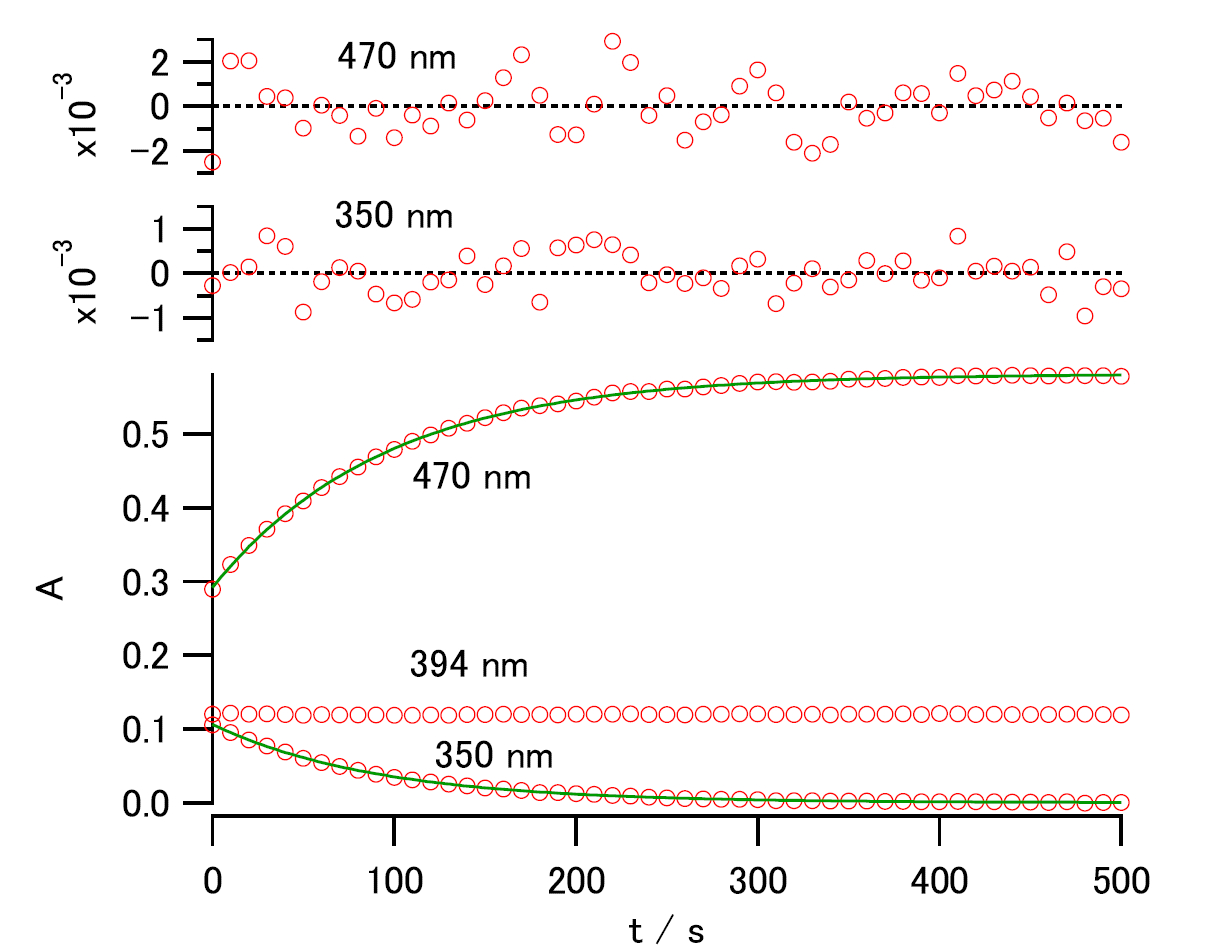
| 図 3-3a NDMAB の熱異性化にともなう吸光度の時間変化と、 非線形最小2乗法による指数関数への当てはめ。 等吸収点(\(\Delta \epsilon\) = 0)の 394 nm では時間変化が検出できない。 | 図 3-3b NDMAB の熱異性化にともなう吸光度の時間変化の 非線形最小2乗法による指数関数への当てはめと残差の表示 |
| 注目波長 | τ / s | 103 k / s-1 |
| 470 nm | 95.1 ± 0.5 | 10.51 ± 0.06 |
| 350 nm | 90.5 ± 0.5 | 11.05 ± 0.06 |
図 3-3a に4-ニトロ-4'-(ジメチルアミノ)アゾベンゼン(NDMAB)の、 470 nm と 350 nm における吸光度の時間変化と、 式 \eqref{eq:abschange} への当てはめの様子を示しました (394 nm は等吸収点で変化なし)。 表 3-1 にはそれぞれの波長の吸光度変化に指数関数を当てはめて得られた、 時定数 τ と速度定数 k を示しました。 どちらの波長の吸光度変化からも、ほぼ同じ値が得られていますが、 350 nm から得られる速度定数の方が 5 % 程度大きくなっています。
この速度定数の違いを、もう少し詳細に検討するために、 当てはめた関数との残差のプロットをしたものを図 3-2b に示しました (こうした機能は Igor Pro に標準で組み込まれており、 Curve Fitting の Output Options の Residual で _auto trace_ を選択すると自動的にグラフに付加されます)。 残差を見てみると、吸光度変化の大きい 470 nm の残差は 350 nm より大きく、 また 350 nm、470 nm ともに吸光度変化の起きている時間帯での残差が少し大きい傾向にあります。 ただし特に傾向だったちがいは認められないようです。 またこの実験は十分長い時間の測定を行っているので、 先の検討で行ったように y0 の値を固定して当てはめても、 得られる速度定数にほとんど変化はありません。
|
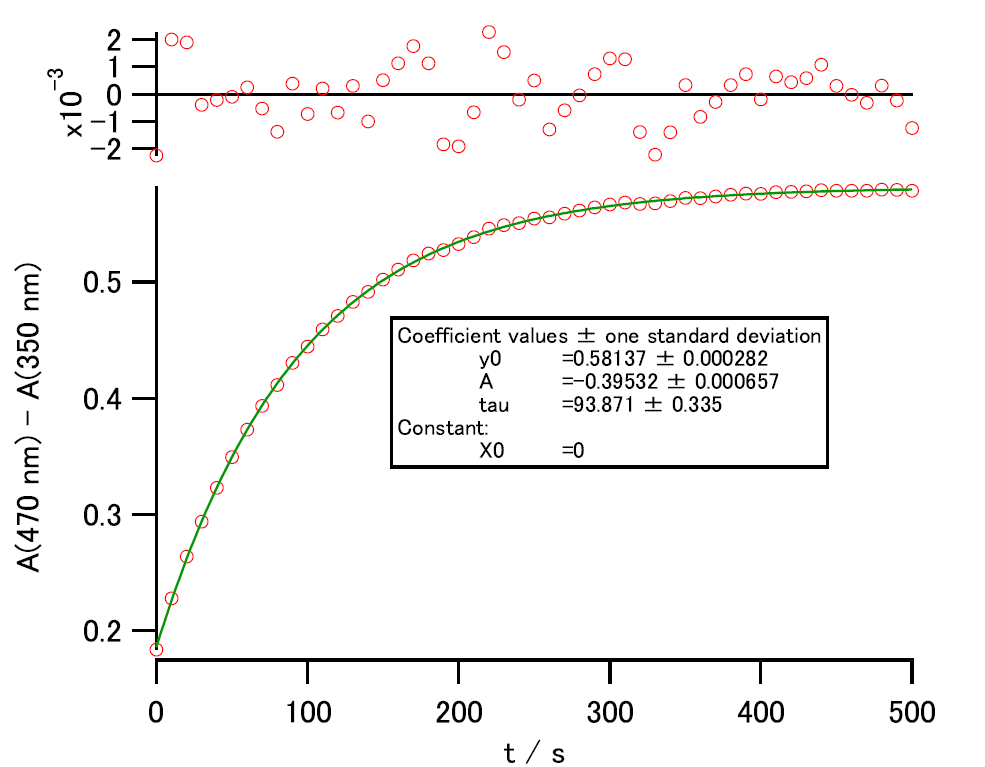
| 図 3-4 NDMAB の熱異性化にともなう 470 nm と 350 nm における吸光度の差 A(470 nm) - A(350 nm) の時間変化と指数関数への当てはめ結果。 |
ここで異性化の速度定数として、どういう値を採用するかは難しいところです。 たぶん 350 nm と 470 nm、両方の結果の平均を取るのが普通でしょう。 表 3-1 で 350 nm と 470 nm 速度定数の標準偏差が同じなので、両者の重みは等しいとみて、 次のようにするわけです:
k = (10.78 ± 0.54) × 10-3 s-1
もう少し測定値にこだわるなら、この場合 350 nm と 470 nm の吸光度の差を取って解析するというのも有力です。 共に式 \eqref{eq:abschange} に従うのなら、その差も同様に指数関数に当てはめられるはずです。 そして差を取ることで、何らかの実験的なノイズが測定値に入っているなら、 打ち消しあってくれることが期待できます。 図 3-4 には A(470 nm) - A(350 nm) を Igor で exp_XOffset 関数に当てはめた結果を示しました。 予期通り当てはめはうまくいっているようで(少しパラメーターの標準偏差が小さくなっている)、 速度定数としては次のようになります(時定数 τ = (93.9 ± 0.3) s):
k = (10.65 ± 0.04) × 10-3 s-1
この手法は今回のように増加する量と減少する量の差を取る場合には、 シグナルが増幅されるので有効です。 けれども共に増加あるいは減少する量の場合には、 シグナルがノイズに埋もれてしまう場合があるのであまりお薦めできません。
とまあ、データのクッキングの話を並べてきたわけですが、 実際には、波長によって速度定数に食い違いが出たりした時は、 まずもう一度実験をやり直すことをお薦めします。 経験的には実験をやり直すと、 食い違いが解消することが多いようです (学生時代、実験室に 「失敗した実験を繰り返せば必ず成功する」 というエピグラムが張ってあったのを思い出します)。 その上で同様の食い違いが出た時には、 もっと本質的な問題(異性体の存在、別の反応機構の存在 etc)が潜んでいる可能性があります。 ともあれデータ処理にあまりにのめり込むと、 得られるであろうものの意味を忘れがちになるので注意が肝要です。
余談ですが 4-ニトロ-4'-(ジメチルアミノ)アゾベンゼンのように 電子供与性の基と電子吸引性の基を持ったアゾベンゼンの異性化の反応速度は、 非常に大きな溶媒依存性を示します。 たとえば溶媒をアルコールなどに変えると、 熱異性化はミリ秒スケールの、まさに瞬時に起きる反応になります。