|
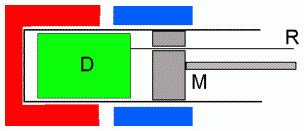
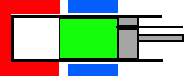
図6.原理的なスターリングエンジンの模式図。赤い部分は高温、青い部分は低温。 |
スターリングエンジンはカルノーが熱機関の原理についての考察を世に問うたよりさらに10年程前、1816年(特許をとった年)にイギリスのスターリング という人によって発明されました*1。 スターリングエンジンにはいろんな型がありますが、考えやすいように、図6のようなエンジンを考えてみましょう。

|
図6.原理的なスターリングエンジンの模式図。赤い部分は高温、青い部分は低温。 |
図6でシリンダーの先のほうは熱せられて高温(900 Kとしましょう)になっており、胴の部分は低温(300 Kとします)に保たれているとします。 この装置でもっぱら動力を生み出すのはピストンMです。 ピストン M とシリンダー、ピストン D を動かす軸 R とピストン M の間は空気がもれないように、はめあいがよくできています。 一方中に入っているピストン D はシリンダーとの間にすき間があって、ピストン D とシリンダーのすき間を自由に空気が行き来できるようになっています。 ピストン D は移動することによってシリンダー内の空気を、外壁によって加熱・冷却させる働きをするものでディスプレーサー(移動体 displacer)と呼ばれます。
このスターリングエンジンの1サイクルは図7の A → B → C → D → A のように進みます。
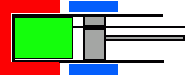
A(1 atm, 1 L, 300K) |
← (4) 温度一定で圧縮 ― |
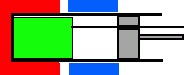
D(1/3 atm, 3 L, 300K) |
|
|
(1) 体積一定で加熱 ↓ |
↑
(3) 体積一定で冷却 | |
|
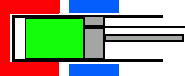
B(3 atm, 1 L, 900K) |
― (2) 温度一定で膨張 → |
C(1 atm, 3 L, 900K) |
(1) 体積一定で加熱、(2) 一定温度で膨張、(3) 体積一定で冷却、(4) 一定温度で圧縮、この4つの過程で1つのサイクルが完結します。ディスプレーサーと主ピストンの動作に注目すると、1/4サイクル分ディスプレーサーが先行して動いています。
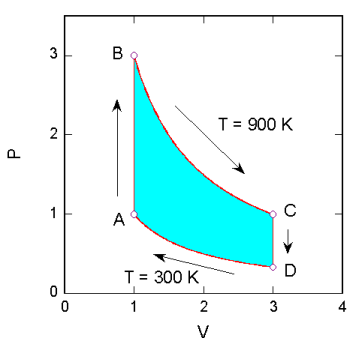
スターリングエンジンの動作をPV図上で書くと、図8のようになります。A→Bの過程で熱が吸収され、C→Dの過程で熱が放出されるのは分かりやすいと思いますが、熱の吸収・放出はB→C、D→Aの過程でも起きています(もし熱の吸収・放出が起きていないとすると、一定温度に保たれない。3章の注4参照)。
|
|
|
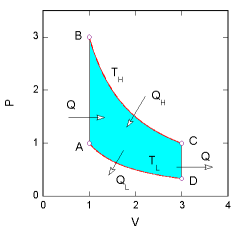
| 図8.PV図上で示した原理的なスターリングエンジンの動作 | 図9.原理的なスターリングエンジンの熱と仕事の収支 |
この熱の出入りを整理すると、A→Bの過程の熱の吸収と、C→Dの過程の熱の放出では、同じ温度差の間で同量の熱の受け渡しが起きるので影響は無視できます*2 。 熱が高い温度から低い温度へ“落ちてくる”という立場からすると、B→C(900 K)で受け取る熱をD→A(300 K)で吐き出すという熱の流れの中で仕事が取り出されたことになります。これをもう少し定量的に考えてみましょう。
B→C、D→A の過程での熱の出入りの大きさを考えるとき、このそれぞれの過程でする(される)仕事が受け取る(与える)熱に等しいことに注目します(温度が一定なので気体の内部に蓄えられるエネルギーは変化しません)。 B→C では D→A に比べて温度が3倍(= 900 K/300 K)なので、同じ体積では圧力も3倍、する仕事の大きさも3倍です。 ですから B→C で外部から与えられた熱を Q(= B→Cで外部にした仕事)とすると、この熱が900 Kから300 Kに"落ちる"ことによって1サイクルで取り出せた仕事は次のようになります。
(最終的に取り出した仕事)= Q - Q/3 = (2/3)Q
この熱Qの仕事への変換効率は次のように評価できます:
(熱の仕事への変換効率)=(最終的に取り出した仕事)/(落ちた熱量) = (2/3) Q/Q = 2/3
ここでは900 Kと300 Kの間で運転されるエンジンを考えたわけですが、一般的に高温THと低温TLの間で動作する熱機関の効率は次のように表現できます。
(熱の仕事への変換効率)= (TH - TL)/TH = 1 - TL/TH
ここではこれ以上触れる余裕がありませんが、カルノーは逆方向のサイクル(仕事をされて低温から高温へ熱を運ぶサイクル)を考えることで熱機関においてこれ以上の変換効率は実現できないことを示しました。この式から、熱機関の熱の最大効率は高熱源と低熱源の温度の比で決まり、低熱源が室温付近の温度で一定と考えれば、高熱源の温度を上げるほど効率が高くできることが分かります。圧力を高くしたり低くしたりするのは、「熱の経済」には無関係なわけです。
最近火力発電所で600℃を超える高温蒸気の利用が進められているようですが、単純に考えると500℃から600℃に上げることで、熱効率は0.52から0.57へ約1割向上することになります。けれどもそれを実現するには、高温に耐える材料の設計など、さまざまな技術的な課題が存在するでしょう。そうした課題の重要さはすでにカルノーが指摘しているところです:
燃料のもつ動力を実際にすべて利用しつくすというようなことは望めない。これになんとか近づこうとする試みも、それが他の重要な点を見過ごさせることになれば、かえって有害である。燃料の経済は、火力機関がみたさねばならない条件の一つにすぎない。多くの場合それは二次的なもので、しばしば機関の確実さ・堅牢さ・寿命・占める場所が小さいこと・建造のための費用、等々を優先させねはならない。おのおのの場合に、便利さと実現されうる経済性とを正しく評価し、もっとも重要なものを単に附随的なものから区別し、もっとも容易な方法によって最良の結果が達成されるように、それらを調和させること、これらをなしうる資質こそ、同胞の仕事を指導し、総合して、人々をなにによらず有用な目的のために協力させるという任を負った人物に要求されるのである。(カルノー、広重徹訳)
*2
同じ温度差の間で同量の熱の受け渡しとはいえ、A→Bの過程の熱の吸収と、C→Dの過程の熱の放出の過程を単純に組み合わせれば、A は 300 K と C は 900 K ですから、A と C の状態を接触させると 600 K で落ち着いてしまって、それ以上変化しないように思われるかもしれません。
ここでのポイントは、A と C の状態を接触させて 600 K にした時に、外部に何らかの仕事をさせることができるということです。
3章2節の最後のところで話題にしましたが、「どのように 300 K と 900 K の状態を接触させるか」が問題です。
仮に 300 K の A に、気体を詰めた 300 K のピストン-シリンダー容器 X を接触させることを考えます。
X を圧縮することで昇温して A と X を 900 K にし、今度は 900 K になった容器 X を 900 K の C に接触。
今度は X を圧縮したのと同じ経路を逆に膨張させることで温度を下げ C と X を 300 K にしたとしましょう。
もしまさつがなければ、X は同じ経路を行き来しただけですから何の仕事もしていませんし、熱の出入りもありません。
結果的に A を 900 K、C を 300 K にして立場を入れ替えただけのことになっています。
A と B を X を介して接触させたわけですが、こう考えると温度が 600 K で落ち着いて止まってしまうという事は起きません。
このあたりの事情のちがいは、900 K と 300 K のものがくっついて 600 K で落ち着いて変化しなくなってしまうのが、2章3節で考えた「釣り合いの下での、ゆっくりした変化」でないことに由来しているのですが、話が長くなるのでこのあたりで・・・。