３．温度と熱

３-１．温度

ある物体の状態を指定するのに、重さ（質量）、圧力などとともに温度が必要であることはみなさんよくご存知でしょう。 特に物質量を与えた時の圧力Pと体積Vと温度Tとの関係は、ふつう状態方程式equation of stateと呼ばれ、理想気体の状態方程式は特に有名です：

ここでnは物質量（単位はmol）、Rは物質によらない定数（気体定数^*1 ）です。 この理想気体の状態方程式に基づき、気体の圧力・体積を測ることで、温度の目盛りを決めることができます（気体温度計）。 この温度（絶対温度といいます）目盛りはSI単位系で採用され、単位はK（ケルビン）、水の凍る温度 0℃で 273.15 Kになるように決められています^*2。 このように決めた温度の目盛りの間隔は、従来の摂氏温度と一致します。

図５. A → B、とB → A で温度条件が違うと、A から出発して A に戻っても正味の仕事はゼロではない。

状態方程式を「熱のする仕事」という観点から見るときの最大のポイントは、圧力が体積だけではなく、温度によっても変化することです。

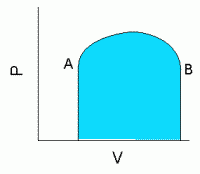
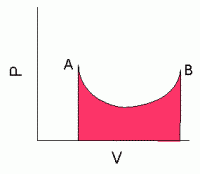
図４の上図のように、ある温度変化をさせることでAの状態から始まってBの状態になり、その後ちがう温度変化を経てAに戻ってきたとしましょう。 同じ状態に戻ってくるのだから何も仕事はしないようにも思えます。 けれども上で述べたように圧力が体積のみの関数でないので、温度変化のようすが違うと、圧力変化のようすも違います。 往きでは水色の部分の仕事をし、返りには赤の部分の仕事をされ、この往復の差引勘定をすると図４の下図のように、輪で囲まれた水色の部分の仕事が外部に対してなされたことになります。

もしかりに圧力が体積のみの関数であれば（バロトロピー流体）同じ線上を往き来するわけで正味の仕事は０です。 往きと返りで温度が違うことによって、初めて正味の仕事が取り出せる。 何でもないようですが、状態方程式にはそうした意味が込められていることに注意していただければと思います。

３-２．熱

温度はいわば「熱さ」の度合い（高い低い）を表すものであったわけですが、「熱さ」を生み出すもとになる「熱」があり、その量（多い少ない）を表すものとして熱量というものがあるはずです。 ですからある物体に含まれる熱の量を次のように考えてもよいはずでしょう。

この熱容量heat capacityというのは、それぞれの物体の熱を受け入れる大きさ・体積を意味し、温度はそうした単位容積当たりの熱量、熱の密度に相当することになります^*3。 そして以前は水 1 gの温度を 1 K上げるのに必要な熱量を1 cal（カロリー）と呼び広く用いられてきました。 なおここで、「物体固有の熱」と呼んだものは、今回のお話ではこれ以上触れませんが、氷が 0℃で融けて水になる時、温度が変化しなくても熱の吸収があるように、温度変化をともなわない「熱」（「潜熱」と呼ばれます）を考えたものです。

けれどもこうした考え方ではうまく説明できないことが多々あります。 たとえば空気を急激に膨張させると温度が下がり、圧縮すると温度が上がります。 これを上の式で説明するには、空気の熱容量が体積の変化とともに変化すると考えねばなりません。 ところが実際にいろんな体積で空気の熱容量を測ってみると、熱容量は体積に依存しないのです^*4。 あるいは物体を温めても重くなるわけではありません。 またあるいは電子レンジでチンとすると温度が上がります。 焚き火の火照りでものが暖まるのは、もともと焚き火が熱いからだと考えて納得できる部分があります。 けれども電子レンジでは特に高温を発生させているわけではありません。 熱を物質のように考えるとすると、よほど特殊な物質を考えねばなりません。

したがって熱は変化にともない放出・吸収される量で、状態の変化の仕方を指定してはじめて意味を持つと考える必要があります。 ですから熱の定義は次のようなものになってきます（構造変化の項は先の潜熱に相当）。

状態の変化の仕方によって熱、熱容量は変化します。 空気の場合、体積一定、圧力一定で温度変化をさせた時、熱容量はそれぞれ温度・密度によらずほぼ一定ですが、圧力一定の熱容量の方が４割程度大きいことが知られています。 こうした態度は「『熱』そのものはない」ということでもあります。 「煮えたぎっているやかんの水は、冷めたやかんの中の水より『エネルギー』を多く含むが、『熱』については議論のしようがない」あるいは 「エネルギー変化の中で力学的・化学的に説明のつかない部分が熱だ」というわけです。

以上述べたように、熱をあたかも何らかの物質であるかのように考えるのは、問題が多々あり、今日の科学では否定されています。 けれどもカルノーが熱機関の動力の秘密を洞察しぬいたように、実際に問題を解決する上では有効な考え方になりえることを見過ごしてはならないでしょう。 たとえば「30℃の水 100 g と 60℃の湯 200 g を混ぜると何度になるか？」という問題を考えて見ましょう。 小学生・中学生ならすぐに、

といった具合にすぐに答えを出します。 ところが熱力学を教わった大学生のお兄さん・お姉さんでは、ウ～ンと考え込んで答えはなかなか出てきません。 今回のお話とも関わりますが、お兄さん・お姉さんが答えを出すには、「この水と湯の混合がいかに行われたか」という情報がなければいけないからです。 けれども、そんなことを考えている間に、お湯は冷めてしまいますよね！

３-３．エネルギー

状態の変化の仕方を指定してはじめて、熱があいまいさのないものとして定義できるわけですが、これは仕事の場合と同じです。 皆さんご存知のことでしょうが、物体に仕事がされた時、まさつによってその仕事の効果をすべて熱に変えることができます。 そしてその熱量は、された仕事に比例することが知られています。この比例係数（ J と cal の換算係数と思えばよい）を熱の仕事当量と呼び 1 cal は約 4.2 Jです^*5。

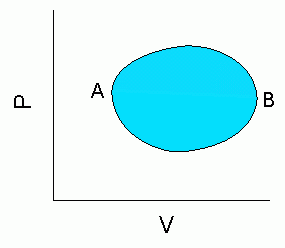
仕事が熱に変わるように、熱を仕事に変えることもできます。そこで熱・仕事を生み出すもっと根源的なものを考え、それをエネルギーと呼びます。 カルノーの時代にも薄々は予感されていたようですが、このエネルギーが保存されるというのがいわゆるエネルギー保存の法則で、今日の科学の基礎にある重要な考えです。 エネルギー保存の法則によれば、図２の下の図のように同じ状態に戻ってきたとすると、した仕事は受け取った熱の総量と同じになります。 カルノーはこの熱の総量を、「受け取った熱」と「与えた熱」に分けて考えることで、さらに熱機関の内実に踏み込んだのでした。

*1
8.314 472(15) J K^-1 mol^-1（CODATA 1998）。

*2
正確には水の三重点（氷と水蒸気と水が同時に共存する状態）の温度を 273.16 Kとして定義されています。また SI では摂氏温度は絶対温度から 273.15 引いたものと定義されています。 水の氷点を0°C、標準沸点を 100°C とする従来の摂氏温度の定義とは実際上は同じですが、精密な測定によると水の標準沸点が 99.97°C ということになっています（ITS-90）。

*3
同じようにことばで比熱 specific heat というのがあります・ 比熱は、比重 specific gravity 同様、ある物体を単位温度だけ温める際に吸収する熱を、基準となる物質（もっぱら水）の場合に比べた比です。 もっとも現在では、比熱は熱容量と等価な言葉として用いられるのが一般です。

*4
体積一定での比熱は空気の場合およそ0.17 cal K^-1 g^-1 = 0.72 J K^-1 g^-1で、ほとんど温度・圧力に依存しません。 ですから温度が一定の条件の下で気体に熱を加えるということは、それと同量の仕事を外部にさせることになります。

*5
今日ではカロリーはこの仕事当量を用いて定義されます。 なお歴史的にカロリーがさまざまに定義されてきた結果、いくつかのカロリーが併用されているので注意が必要です。 化学・食物学の分野では 1 cal = 4.184 J（熱化学カロリー。cal_thと表記）が用いられますが、4.1855 J （15℃カロリー。cal₁₅）、4.1868 J （国際蒸気表カロリー。cal_IT） は国際的にも用いられ、国内では今も一部4.18605 J （「旧計量法カロリー」。1 cal = (1/860)×3600 J） が生き残っています。