お話のはじめに「仕事」ということばを、少しはっきりさせておきましょう。 以下では「仕事」の大きさを次のように考えます。#
「する仕事」=(動かす力)×(動かした距離)
SI単位系では仕事の単位はJ(ジュール)で、物体に1 Nの力(単1の乾電池の重さがこの程度)を加えて1 m動かす仕事に相当します。 たとえば60 kgの人を1 m持ち上げるのであれば、60 kgの人に働く重力はおよそ600 Nですから600 Jの仕事ということになります。

|
この仕事の定義をもとに、油圧式のピストンを使った機械のする仕事を考えてみましょう。 ピストンに働く力は(圧力)×(断面積)ですから仕事の大きさは
「する仕事」=(圧力)×(断面積)×(動かした距離)
=(圧力)×(体積変化)
で表現されることになります。蒸気や空気のように形を持たない流体のする仕事を考える上でこの表現は便利です。
|
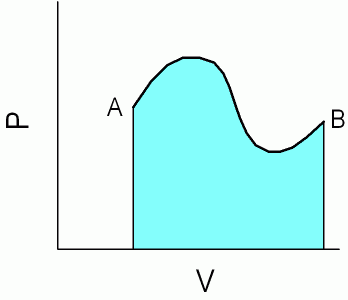
仕事を(圧力)×(体積変化)で表そうというわけですが、仕事をしている間に力・圧力が変化したらどうなるでしょう? そうした場合には、時々刻々、その時々の(圧力)×(体積変化)を足しこんでいけばよいでしょう。 これはグラフで考えると、図3のようにAからBまで体積Vが変化する道中の圧力Pの変化のようすがわかっておれば、その間に外部にした仕事が、図の水色をつけた部分の面積を求めることに相当するということです(逆にBからAまで体積が変化するとすると“された仕事”がわかるわけで、この時には“マイナスの仕事をした”ことになります)。 なお単位時間当たりどれだけの仕事をするかというのを「仕事率」とよび、SI単位系の単位はW(ワット)。自動車などでよく使われる馬力はこの仕事率の単位で、1馬力は約740 Wです。
以下では特に注意しませんが、仕事は力がほぼつりあった状態でゆっくりなされ、同様に熱のやり取りもほぼ温度が等しい条件の下でゆっくり起きるもの(準静的過程)とします。 力がほぼつりあった状態で仕事が行われるというのは、内外での圧力が同じ、つまりまさつがないということです。 また熱のやり取りがほぼ同じ温度、温度がつりあった状態で行われるというのは、カルノー流のたとえで言えば、熱の落下に対するまさつがないことに相当します。
#
ここではある流体が外部の物体に「する仕事」に注目して議論を進めていくことにします。いわば次のような表式に立って議論しようとするわけです:
(熱) = (エネルギー変化) + (する仕事)
一方、今日の標準的なエネルギー保存則の表記は、
(エネルギー変化) = (流入する熱) + (される仕事)
というものです。
どちらの表式でも符号にさえ注意すれば同じことのようですが、「熱」の概念的な位置づけ、あるいは系の性格付け(能動的か、受動的か)にちがいがあります。
今回のお話の文脈には、今日の標準の取り扱いはそぐわないと考え、敢えて「する仕事」という観点を取っています。
なおこの件に関わって注意しておくと、「AがBにする仕事」は「AがBからの力に抗して行う仕事」という意味ですが、「AがBにされる仕事」は「Aからの力に抗して行われたBの仕事」ではなく「Bからの力をもってAに対して行われた仕事」という意味です。 同じように思われるかもしれませんが、一般にはAがBに及ぼす力とBがAに及ぼす力は等しくありません。 両者の力が等しくないので運動が始まり、その運動の中で「仕事」も行われるわけですから。 (2005.5.9 付記)
* 注意深い方は、この図で体積の増加とともに圧力が増加する部分があることに違和感をもたれるかもしれません。 膨張して圧力が増えるという現象は温度一定の条件では起こりません(いわゆる「機械的な不安定性」を起こす)。 けれども温度上昇にともない体積が増加するといった過程(そこで圧力の増加も起きる)を考えていただければ、図のような変化も許されることに留意ください。