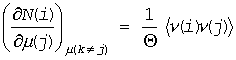(F1)
(F2)
OZの論文におけるOZ方程式の導出にはいささか疑義があります。たとえば(C1)式で、ν(i) についての高次の項を除いたことの当否、あるいは g(0, ν(0)) を任意であるとして 0 とおくことは正しいのでしょうか。このあたりを探るために、OZ方程式に対するぼくなりの熱力学的な説明を示しておきましょう。
２つのセル i と j に存在する粒子を、それぞれ分子種 i、j と見なしたとしましょう。（このように異なる場所に存在する分子を異なる分子種と見なすことに抵抗を覚える方がおられるかもしれませんが、そもそも分子種という概念自体が、何らかの操作に基づいて人間の都合で作った概念であることに注意してください。）すると粒子数のゆらぎの表現から温度一定の条件のもと、次の関数 G(i, j) を考えることができます（この G は(E1)式の G(k) とはちがうので注意）。
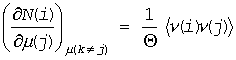(F1)
(F2)
この逆に、粒子数変化に対する化学ポテンシャルの応答 H(i, j) を考えることもできます。
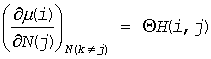(F3)
ここで２つの関数 G(i, j) と H(i, j) をそれぞれ行列要素とする行列（ヤコビ行列）を考えれば、互いに逆行列の関係にあります。
(F4)
この式の導出については
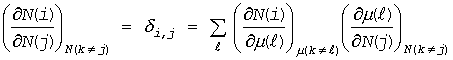(F5)
であることに注目ください。
実はオルンシュタイン-ゼルニケの式は、この式と等価なのです。この事情を少し説明しましょう。
理想気体について関数 G、H を考える（下付き ０ で示します）と、容易に次のような関係式を得ることができます（理想気体については、μ =μ* + Θ ln N であることを思い出していただければよいでしょう）。
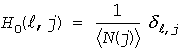(F6)
(F7)
そこで G と H それぞれを、次のように理想気体の部分 G0、H0 と非理想性の部分 Γ(i, j)、-c(i, j) に分けて書いてみます。
(F8)
(F9)
この式を上の式に代入すれば
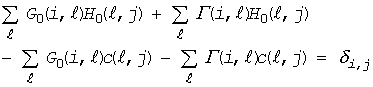(F10)
先の(F6)と(F7)式に注意して整理すると、次の式を得ます：
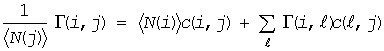(F11)
ここで新たに関数 h(i, j) を次のように定義してやります。
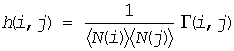(F12)
そうすると、結局、次式を得ます。
(F13)
一つのセグメントの大きさを十分小さくしたときには、右辺の総和の部分を積分に移行できて次式となります：
(F14)
特に系が均一ならば、次の式、OZの積分方程式、(C8)式を得ることができます（ρh(r) が g(r)、ρc(r) が f(r) に対応）：
(F15)
このように、OZ式で注目しているのが化学ポテンシャルに対する粒子数の応答、あるいはその逆であったと考えると、OZの論文での２つの関数、fとgの性格付けもより明確に理解できるのではないでしょうか。(C1)式で高次の項が出てこないのは、そもそもが１次の微分量を考えているからなのです。また関数fを単に「分子間の相互作用の効果のものさし」とだけ考えていたのでは、たとえば剛体球分子を考えた時、剛体球の直径より内側で関数fが有限の負の値をとることはちょっと説明できないでしょう。こうした話は言い出すと長くなるので、このあたりにしておきます。
なおここで展開した議論は、汎関数微分を用いた方法 [4] と等価なものです。人によると密度汎関数を用いた記述の方が、よりエレガントで好ましいものに見えるかもしれません。けれどもぼくにはOZの論文の持っていたより直截な見通しを損なうように思え、さらに言うと、ぼくの化学者としての感性になじまないものを感じて、好みではありません。