さてOZの論文では光散乱に注目して、fやgをフーリエ変換した形でkの関数としてもっぱら考えたのですが、実空間で r の関数として考えたらどうなるでしょうか。論文 [2] の中で、ゼルニケはこの問題に一つの答えを与えました。なおこの論文では、ローレンツ(H. A. Lorentz)による電子による光の散乱に対する理論 [15] を取り入れて、臨界点での光の吸収についても論じているのですが、ローレンツの議論も知らないぼくにはその意義をよく捉えられません [16] ので、ここでは関数 g(r) (今日的には、全相関関数 h(r) に数密度をかけたもの)の実空間での挙動に絞って紹介します。
すでに g(r) が f(r) に比べて、距離についてゆっくり変動するであろうことは見ました。ですから十分遠いところでは f(r) は 0 と見なせ、g(r) は f(r) が 0 でない値を取る領域(E節の最後で評価した R 程度)では、ゆっくり変動する関数とみなすことができるでしょう。この考えを、(C8)式のたたみこみ積分に適用して、十分大きな r について g(r) を評価することを考えます(以下ではゼルニケの原論文の導出を簡略化してあります)。
距離 r を十分長く取れば、(C8)式の右辺の f(r) は無視できます。
ついで、f(r') が 0 でない値を取る領域に注目すれば、g(|r - r'|) を r の周りで展開することができるでしょう。
ここで g(r) の1階微分の項は f(r') が等方的なので落としました。この2階微分までの項を取って、次の g(r) についての微分方程式を得ます(F(0)、ε については(E5)-(E7)式参照):
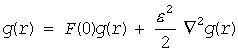 (G3)
(G3)
この方程式を解くと、大きな r での解として
をえます。ここでκは
で与えられます(三次元の方程式∇2q(r) = q(r)で、q = p/r とおくと、1次元の微分方程式 d2p/dr2 = pになることと、g(r) の全空間にわたる積分が G(0) になり(E4)式を満たすことに注意する)。
この式から κ-1 が分子の分布の相関距離(電解質溶液で出てくるデバイ距離と形式的には同じ形で興味深いのですが、内実は異なる)を与えることになります。温度・圧力を変えて臨界点に近づけば、F(0) は 1 に近づき、相関距離は発散していくことになります。
密度ゆらぎを表わす関数 g(r) が遠方で(G4)式のような形を持つことは、(E7)式を(E2)式に代入し G(k) の逆フーリエ変換を行っても得られます。けれどもここで示された実空間での議論は、短距離に止まる分子間相互作用の効果が繰り込まれて、長距離にわたる分子の凝集をもたらす仕掛けを、より生き生きと見せてくれたものといえましょう。