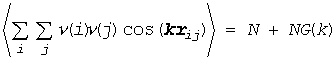 (E1)
(E1)
周囲のゆらぎを固定した時(→ f )とゆらいでいる時(→ g )の、ある場所の粒子数変化が他の場所の粒子数ゆらぎに及ぼす影響を考えて得られたOZの積分方程式(C8)ですが、このような表現をして何かいいことはあったんでしょうか?2つの関数 f と g が導入されたといっても、OZ式だけを眺める限り両者には(符合を除けば) f と g には特に違いがあるわけではありません。
このOZ式が意味を持つのは、導入された2つの関数 f と g の性格付けに関わってきます。先の考察から f は分子間相互作用の到達する程度の距離で値を持つ関数でしょう。一方、g は分子間相互作用による密度の変動が、さらに他の場所の変動を引き起こし、広範囲に広まっていく効果を含んでいます。
こうしたアイデアと、光散乱について重要なのが、微小領域間のゆらぎの相関であったことを結び付けて、考えを進めて見ます。先の(B5)式と密度のゆらぎの相関の式を比べると、次のような関数が重要であることが分かります(論文中では G(k) は Gc と表記されています)。
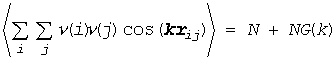 (E1)
(E1)
これは密度ゆらぎのフーリエ変換。今風に言えば「構造因子」と言われるもの(S(k) = G(k) + 1)に対応しています [14]。フーリエ変換をほどこせばOZ式の第2項はたたみ込み積分の形をしていて、(C8)式は次のように整理できます。
先に G(0) と等温圧縮率の関係はみました。
臨界点に近づくにつれ圧縮率は非常に大きくなりますから、臨界点近傍では G(0) もどんどん大きくなります。一方、(E2)式から F(0) については
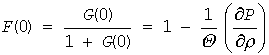 (E4)
(E4)
これは臨界点では 1 になる量です。この G(0) と F(0) の挙動からも、g(r) が長距離に及ぶものであるのに対し、f(r) が分子近傍でのみ 0 と異なる値をとる関数であることがわかります。さて、光の波長程度の長さ(数百nmなので、分子が 1 nmぐらいとすれば数百個入る)に相当する k を考えれば、cos kr は非常に小角での散乱(θ = π - φ ~ 0)でない限り、f(r) よりもっと緩やかに変化するでしょう。ですから、cos kr を k のベキで展開して考えます。
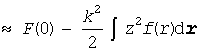 (E6)
(E6)
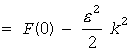 (E7)
(E7)
ここで、ε はおおよそ f(r) が値を持つ範囲を与える長さ(分子間引力の及ぶ範囲)の2乗に相当します。この式を、先の光散乱の式に適用すると、次のように書けます。
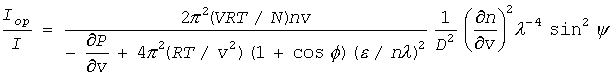 (E8)
(E8)
ここでは半角公式を使って、2 cos2(φ/2) を 1 + cos φ にしています。また(B11)式でも触れたように、たぶん分子にある n は2乗でないといけないのですが、原論文のままにしてあります。この式から、臨界点に近づくにしたがって、散乱光の強度が波長の4乗から2乗に反比例するようになること、そして前方(φ~π、θ~0)により強く散乱されるようになることがわかります。特に臨界点では、dP/dv は0になるので、
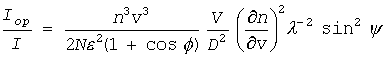 (E9)
(E9)
という式を得ます(ここでも分子は n4v3 でないといけないが原論文のまま。また因子1/2が抜けているので補いました)。臨界点で散乱強度は発散せず、有限に止まるわけです。
このことはゼルニケの実験でも示された [9] ところのようです。彼は温度を臨界温度 TK に近づけていった時 I/Iop が直線的に減少していくが、温度を臨界温度に外挿したとき、それが 0 になるのは臨界温度より 0.012 低いところでした(原論文では、T - TK = 0.012 となっています。トリエチルアミン-水のような下部臨界温度のある混合系の相分離の臨界点で行ったのかもしれませんが、1916年のゼルニケの論文 [2] から察するに-0.012の誤りでしょう。直線的に減少していくのは、今日風に言えば臨界指数 γ がほぼ1 (彼らの採用したファンデルワールス状態方程式なら 1。今日知られている値は 1.25 ぐらい)であることに対応。なおここでの温度の単位は何かよくわかりません。正確なところはゼルニケの学位論文 [9] に当たる必要があるようです)。
ここから ε/λ を算出すると 0.0022、ε は 1.2 × 10-7 cm となりました(用いた光の波長は 550 nm ということになるのですが、どんな光源を用いていたのでしょうか?ナトリウムのD線は 590 nm で若干ちがいます)。また f(r) が、r < R で一定の値、それ以外で 0 とすれば、R は √5 ε、2.7 × 10-7 cm となります(εが r2 ではなく、z2 についての積分であることに注意します。(E6)式)。どのような系について検討したのか定かではありませんが、これは今日想定される、分子間力の及ぶ範囲と同程度といえるでしょう。