さて光の散乱が密度のゆらぎに深く関わっていることを見たわけですが、今度は系全体の密度のゆらぎと流体中の局所構造とのかかわりを考えてみましょう。ある体積 V の領域を考え、そこに見いだす分子数 N の揺らぎと、局所的な密度の揺らぎの関わりを考えます。そのために、この領域を同じ体積 δv を持つ微小なセルに分割したとします。かりにセルの体積が極めて小さく、見いだす分子数がせいぜい 1 個であるとすれば、i 番目のセルに見いだす分子数 N(i) が 0 か 1 の値しか取りませんから
です。ですから i 番目のセルに見出す分子数の分散は次のようになります((δv)2 はあまりに小さいので無視)。
一方、系全体の粒子数のゆらぎは
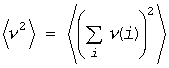 (D3)
(D3)
![]() (D4)
(D4)
ここで第1項は(D2)式から、全粒子数 N に等しく、第2項は先ほどの関数 g(i, j) を用いて評価でき、系全体の粒子数の揺らぎは次式で評価できることになります。
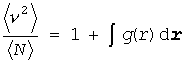 (D5)
(D5)
この式と先の圧縮率の式 (B10) を組み合わせたものを、今日「圧縮率方程式」と称します。