空気による光の散乱(空はなぜ青い)については、レーリー(Rayleigh)の有名な理論があり、OZの論文(あるいはそれに先行する研究)はそれを当然の前提としています。このレーリーの議論を説明するには、電磁波の放射に対する基礎的な知識が必要になるのですが、液体の統計理論を勉強しようという人は、そうした基礎的な素養を欠いていることが多い(少なくとも、ぼくはそうです)ようです。そこでまず光散乱についての、ぼくなりのラフなスケッチを示すことにします。
レーリーの光散乱の議論は、大きく
という3つの段階からなっていると見ることができます。
光というのは電磁波、つまり電場と磁場の振動ですから、光がやってくるということは、いわば変動する電場が働くことだと思ってよいのです。電場が働けば、物質は静電誘導で分極し、誘起双極子モーメント Mind が生まれます。電場があまり強くなければ双極子モーメントの大きさは働く電場に比例すると見なせ、その比例定数は分極率αで評価できます。そしてこの双極子モーメントは光の振動数(ω/2π)に応じて振動します。
なお分子の姿かたち(分極率の異方性)や内部構造(振動状態・電子状態など)、摩擦(緩和)などを考えないといけないようなケースでは議論は単純ではありません。ここではそうした効果は無視します。
電気のスイッチを切ったり入れたりする時にラジオにノイズが入るように、電気の流れの様子が変化すると、その流れの変化速度に応じて電磁波、光が発生します。双極子が振動するということは、電気の流れが周期的に変動することですから、同様に電磁波の放出をともないます。これが散乱光の素になります。この散乱光の電場 Escat は、双極子モーメントの変化速度の変化、時間についての2階微分に比例します。
ここでψは双極子モーメントの軸から測った角度です(光の偏光方向に対する角度と思えばよい)。光は横波ですから、電場の振動する方向と垂直方向に強く放射され、その角度依存性は正弦関数sineで評価されるというわけです。そして光の強さ(単位時間あたりのエネルギー)は、電場の強さの2乗に比例しますから、散乱される光の強さIscatは振動数の4乗に比例(波長の4乗に反比例)することになります。
なおOZの論文では取り上げられていませんが、無偏光の場合、この式を偏光方向について平均化すると、散乱方向に対して 1 + cos2θ の依存性が現れ、前方・後方に対称的に散乱が起きることになります。
さて(2)の議論は、物質のある領域からの散乱光の話でした。実際には同じことが物質を構成する無数の微小領域(分子を考えてもよい)について成り立ち、そこから出てくる散乱光を総和したものを観測するわけです。ここで散乱光の互いの干渉の効果を評価する必要があり、ここからが OZ の議論でも重要になるところです。
もしすべての微小領域がまったく同じ分極率をもったものとして振舞うならば、散乱光は互いに干渉しあってどんどん弱くなっていくでしょう(完全に均一なら散乱は起きない)。けれども、もし、それぞれの微小領域で分子運動によって分子の数に変動があり、分極率が平均からいろいろにゆらいでおれば、事態は違ってきます。このあたりの事情を式で書いてみれば次のようになります。
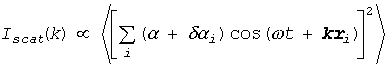 (B4)
(B4)
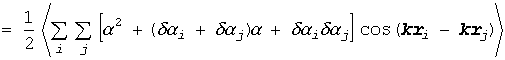 (B5)
(B5)
ここで積和の公式を用い、時間とともに変動する項(cos(2ωt + k ri + k rj))は時間平均を取ると 0 になるので落としました。この(B4)式の [ ] の中の項を見てみると、α2 の項は cos(k ri - k rj) を平均すると 0 になるので落とせます(まったく均一な分布(連続体)をしておれば散乱は起きない)。また分極率のゆらぎの1次の項は平均するとこれも 0 になるはずです。ですから、光の散乱を与えるのは、分極率のゆらぎの相関で、次のように表現できます(相対距離を rij で表記)。
![]() (B7)
(B7)
レーリーの光散乱の議論では希薄な気体を考えているので、微小領域の間のゆらぎに相関がないと考え、自己相関のみを考えます。そして微小領域では分子が存在するかしないか、0か1かという選択肢の中で分極が起きるので、その度合いは数密度 ρ に比例することになります(後出の(D2)式参照)。
なお、OZの原論文では光の位相の部分 ωt + k r を
としていますが(n は屈折率。原論文ではμを使っている)、これを簡単のため今風の表式に焼きなおしました。ここで k は、入射方向と散乱方向の波数ベクトルの差です。なお今は、φ を π - θ と置くのが普通です( k = (4π/nλ) sin(θ/2) となります)。
この気体の光散乱の議論を、もっと密度の高いものに適用しようとした時、分極率の揺らぎ(∝ 密度・粒子数の揺らぎ)は、分子間相互作用の結果、単純ではなくなります。ところで、この粒子数Nのゆらぎは、系の等温圧縮率(1/ρ)(dρ/dP) と関係づける事ができます(OZの原論文には丁寧な解説はありませんが、結果は示されています。アインシュタインがこうした表式を導入したらしい [7] )。
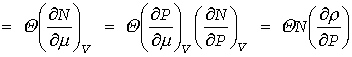 (B10)
(B10)
ここでギブズにならって、Θはボルツマン定数に絶対温度をかけたもの kBT を示します。なお粒子数ゆらぎを、粒子数の化学ポテンシャルの微分で表現するのはすでにギブズが示しているところ [13] です。(それをギブス-デュエムの関係を使って、圧縮率と関連付けたのは誰なんでしょうね?)
こうしたところから、キーソム、アインシュタインは次のような散乱強度の式を導いたようです:
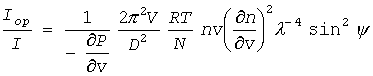 (B11)
(B11)
ここで D は観測地点までの距離、N は分子数、V は体積、v は分子あたりの体積(ρの逆数。V/N)、n は屈折率で、屈折率の2乗(誘電率に相当)から1を引いたものが分極率に相当します。臨界点に近づくと体積弾性率はどんどん小さくなります(圧縮率はどんどん大きくなる)。この式によると、臨界点に近づくと光の散乱が大きくなって臨界タンパク光が観察されるようになり、臨界点では発散するというわけです。
なおこの式の表記はOZの論文のものをそのまま引き写しました(屈折率の表記をμから n に改めた以外)。式中 nv のところは、たぶん n の2乗でないといけないのですが、そのままにしてあります(後出の(E8)式でも n の1乗なので、単なる誤植ではなく、著者自身が何かの勘違いをしていたか、あるいはもっと深い事情があるのかもしれません)。こうした内容的な問題以外に、この式は分子あたりの体積 v と系の体積 V がない混ぜられて、いささかゴタゴタしています。この事情は定かではありませんが、RT/N という表記(つまりギブズのΘ、kBT)に何かこだわりがあったためのように思われます。(dv/dP でなく dP/dv にしたのは、後出の(E8)式、OZの光散乱の式との関係でしょう)
ここまで見てきたところで、OZの論文で何が議論されるのかもう分かりますね。(B5)式から(B6)式のところで無視した微小領域のゆらぎの間の相関、そしてそのk依存性が問題なわけです。