2025.12
吉村洋介
化学実験法 II
確率と統計のはなし
3.平均と分散
ランダム変数の分布関数が与えられた時、その特徴をいくつかの数値・特性値に凝縮させて理解することができれば便利である。
そうした特性値として平均と分散がある。
ランダム変数 \(x\) の重みである分布関数 \(f(x)\) を付けて、
関数 \(q(x)\) を全区間で積分したものを \(\avg{q(x)}\)と書き、\(q(x)\) の平均あるいは期待値と呼ぶ 。
またこれは積算分布関数 \(F(x)\) を用いて表すこともできる。
\begin{equation}
\avg{q(x)} = \int_{-\infty}^{\infty} {q(x) f(x) \rmd x}
\left[ = \int_{0}^{1} {q(x) ~\rmd F(x)} \right ]
\label{eq:mean0}
\end{equation}
\(\avg{x}\) を簡単のため \(\mu\)(あるいは \(\mu_x\))で表わすこともある。
\begin{equation}
\avg{x} = \mu = \int_{-\infty}^{\infty} {x f(x) \rmd x}
\left[ = \int_{0}^{1} {x ~\rmd F(x)} \right ]
\label{eq:mean1}
\end{equation}
平均は分布の中心位置を示すものと考えてよい。
また \(x\) の \(n\) 乗の平均 \(\avg{x^n}\) を \(x\) の \(n\) 次のモーメントと呼び \(\mu_n\) と表記する。
なお分布関数のフーリエ変換 \(\hat{f}(\omega)\) は次のように表せる(分布関数の特性関数 characteristic function と呼ばれる)。
\begin{equation}
\hat{f}(\omega) = \int_{-\infty}^{\infty} \rme^{\rmi \omega x} f(x) \rmd x = \avg{\exp(\rmi \omega x)}
\label{eq:mean0ex}
\end{equation}
一般に \(N\) 個のサンプル \(x_1, x_2, \cdots, x_N\)(≥ 0)の「平均」としては、
算術平均 \(AM\)(相加平均)、幾何平均 \(GM\)(相乗平均)、調和平均 \(HM\) の3つがよく知られています(「ピタゴラス平均」。\(AM \ge GM \ge HM\))。
\[
AM = \frac{x_1 + x_2 + \cdots + x_N}{N},~~~~~~
GM = \sqrt[N]{x_1 x_2 \cdots x_N},~~~~~~
HM = \frac{N}{x_1^{-1} + x_2^{-1} + \cdots + x_N^{-1}}
\]
これ以外にも気体分子運動論で、「根平均2乗速度」に出会ったことがあるでしょう。
いろんな平均の取り方があるのですが、
このおはなしで「平均」は式 \eqref{eq:mean0}、
算術平均 \(AM\) に相当するものとします。
化学反応速度では、反応物の平均寿命がしばしば話題になります。
1 次反応 A → B では反応物の寿命 \(t\) は指数分布に従います:
\[
f(t) = k \rme^{-kt}~~~~(t \ge 0)
\]
あるいは時刻 \(t\) までに分解する確率は積算分布関数を用いて次式で表されます:
\[
F(t) = 1 - \rme^{-kt}~~~~(t \ge 0)
\]
ここで \(k\) は反応速度定数で、指数分布の \(n\) 次のモーメントは、次式で与えられます(ラプラス変換の公式を思い出そう!):
\[
\mu_n = \int_0^{\infty} t^n k \rme^{-kt} \rmd t = \frac{n!}{k^n}
\]
平均寿命 \(\tau\) は \(\avg{t} = \mu_1 = 1/k\) になります。
確率分布の平均、モーメントは常に存在するとは限らず、例えば 2 次反応
2A → B の場合、反応物 A の寿命 \(t\) の分布は次式に従います:
\[
f(t) = \frac{k c_0}{(k c_0 t + 1)^2} ~~~~(t \ge 0)
\]
ここで \(k\) は 2 次反応速度定数で、\(c_0\) は A の初濃度です。
ここから寿命(1 次のモーメント)を計算すると、発散してしまいます:
\[
\avg{t} = \int_0^{\infty} \frac{k c_0 t}{(k c_0 t + 1)^2} = \left[ \ln (k c_0 t + 1) + \frac{1}{k c_0 (k c_0 t + 1)} \right]_0^{\infty} \to \infty
\]
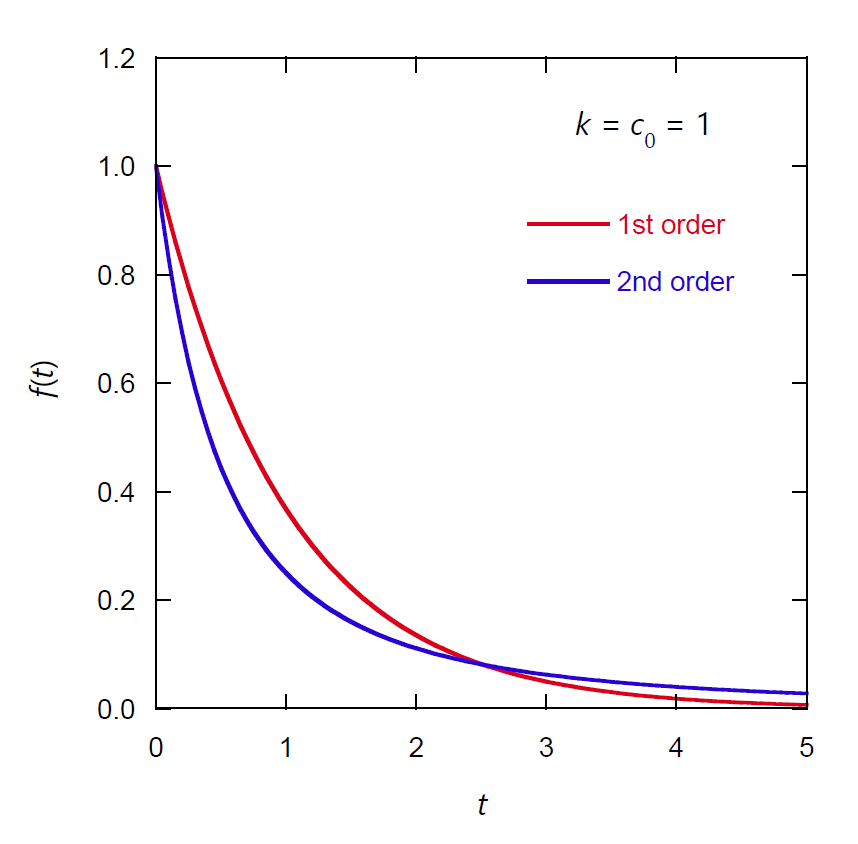
それぞれの寿命の分布関数を図 1 に、積算分布関数を図 2 に示しました。
2 次反応の場合の分布関数が、裾を長く引いていることが分かります。
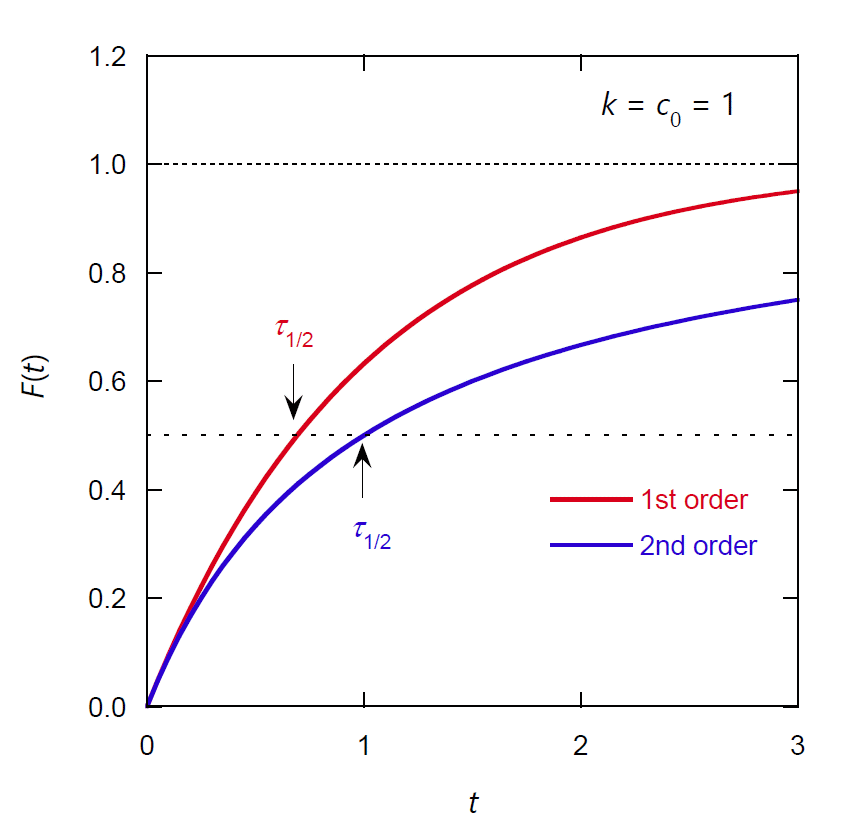
また積算分布関数で \(F(t) \)= 1/2 となる時刻 \(t\) は半減期 \(\tau_{1/2}\) と呼ばれ、
統計の分野の言葉で言えば、寿命分布のメディアン(中央値)に相当します。
|
|
|
図 1. 1 次反応と 2 次反応における反応物の平均寿命の分布関数。
|
図 2. 1 次反応と 2 次反応における反応物の平均寿命の積算分布関数。
1 次反応の半減期 \(\tau_{1/2}\) は ln 2/k = 0.693/k、
2 次反応は 1/(k c0)。
|
平均については次のような関係が成立する。
\begin{equation}
\avg{a x + b} = a \avg{x} + b ~~~ \mbox{(\(a\) と \(b\) は定数)}
\label{eq:mean2}
\end{equation}
\begin{equation}
\avg{x + y} = \avg{x} + \avg{y} ~~~ \mbox{(\(x\) と \(y\) はランダム変数)}
\label{eq:mean3}
\end{equation}
特に \(x\) と \(y\) が統計的に独立であるなら、\(x\) と \(y\) の積について次の関係式が成立する。
\begin{equation}
\avg{xy } = \avg{x} \avg{y} ~~~ \mbox{(\(x\) と \(y\) は独立)}
\label{eq:mean4}
\end{equation}
平均は分布の中心位置に相当するものを与えるのに対し、
分散・標準偏差は分布がどの程度の広がりを持っているかを与える。
ランダム変数 \(x\) の分散は \(\sigma^2\)(あるいは \(\sigma_x^2\)、 \(\sigma_{xx}\))で表され、
ここでは \(\var{x, x}\) あるいは \(\var{x^2}\) という表記も用いる。
ここで \(\var{x, y}\) は次の量に相当する。
\begin{equation}
\var{x, y} = \var{xy} = \avg{xy} - \avg{x}\avg{x}
\label{eq:mean5}
\end{equation}
\(x\) の分散 variance は次式のように定義される:
\begin{equation}
\var{x, x} = \var{x^2} = \sigma_x^2 = \avg{x^2} - \avg{x}^2
\label{eq:mean6}
\end{equation}
先に導入した \(\var{x, y}\) はランダム変数 \(x\) と \(y\) の共分散 covariance と呼ばれる。
共分散に関わっては次の関係式が成立する(\(x\)、\(y\)、\(z\) はランダム変数。\(a\) は定数)。
\begin{eqnarray}
\var{x, y} &=& \var{y, x}
\label{eq:mean7}\\
\var{x, a} &=& 0
\label{eq:mean8}\\
\var{x+y, z} &=& \var{x, z} + \var{y, z}
\label{eq:mean9}\\
\var{ax, y} &=& a\var{x, y}
\label{eq:mean10}
\end{eqnarray}
したがって次式が成立する(\(\mu = \avg{x}\))。
\begin{equation}
\var{x, x} = \var{x - \mu, x - \mu} = \avg{(x - \mu)^2} \ge 0
\label{eq:mean11}
\end{equation}
分散は平均の周りの2次のモーメントに相当し、負にはならない。
分散の平方根を標準偏差 \(\sigma\)(あるいは \(\sigma_x\))と呼ぶ。
\begin{equation}
\sigma_x = \sqrt{\var{x^2}}
\label{eq:mean12}
\end{equation}
同様に共分散 \(\sigma_{xy}\) は次式で表現することができる。
\begin{equation}
\sigma_{xy} = \var{x, y} = \var{x - \mu_x, y - \mu_y} = \avg{(x - \mu_x)(y - \mu_y)}
\label{eq:mean13}
\end{equation}
共分散が正であれば、\(y\) は \(x\) の増加にともなって増加し、
負であれば減少する傾向にある。また \(x\) と \(y\) が統計的に独立であれば共分散はゼロになる。
\begin{equation}
\var{x,y } = 0 ~~~ \mbox{(\(x\) と \(y\) は独立)}
\label{eq:mean14}
\end{equation}
共分散がゼロの場合 \(x\) と \(y\) は無相関であると呼ぶ。
無相関であっても統計的に独立であるとは限らないが、統計的に独立であることの重要な指標となる。
また統計的に独立なランダム変数の和 \(z = x + y\) の分散は、\(x\) と \(y\) それぞれの分散の和になる。
\begin{equation}
\var{z^2} = \var{x + y, x + y} = \var{x, y} + 2 \var{x, y} + \var{y, y} = \var{x^2} + \var{y^2}
\label{eq:mean15}
\end{equation}
モーメントや分散に関わって、少し具体的に眺めておきましょう。
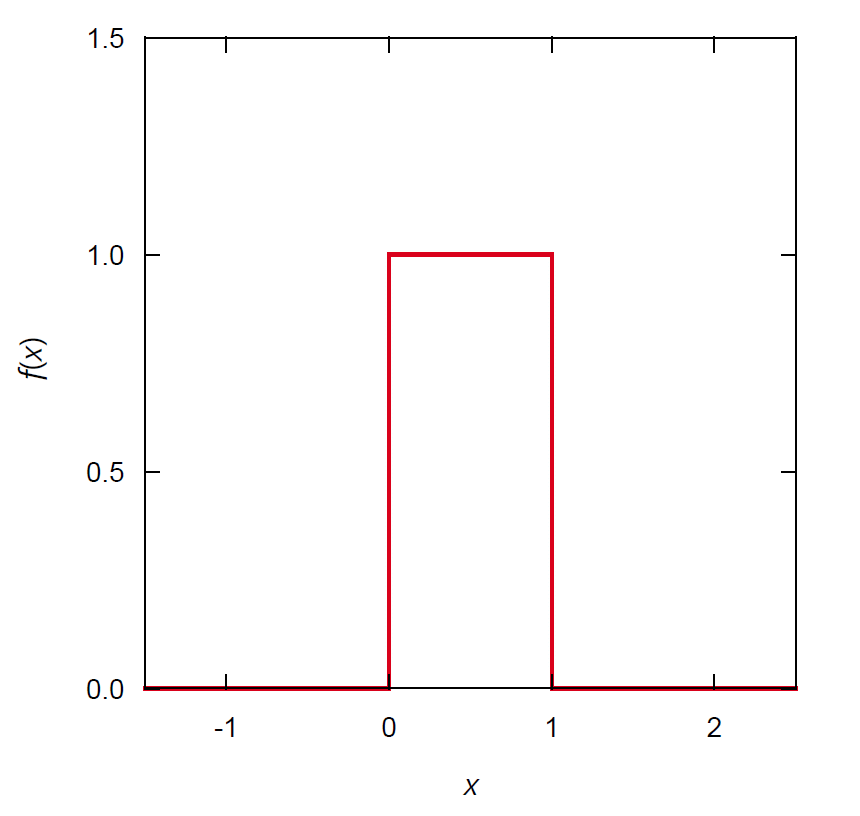
計算機では、次のような [0, 1) 区間の一様分布 uniform distribution(矩形分布 rectangular distribution とも)に従う乱数がよく用いられます:
|
|
図. [0, 1) 区間の一様分布の分布関数
|
\[
f_x(x) = \left\{
\begin{array}{rl}
1 & 0 \le x < 1\\
0 & \mbox{その他}
\end{array}
\right.
\]
この分布関数について、モーメントを求めると次のようになり:
\[
\avg{x^n} = \int_0^1 x^n \rmd x = \frac{1}{n+1}
\]
分散は 1/12 になります:
\[
\sigma^2 = \avg{x^2} - \avg{x}^2 = \frac{1}{3} - \left( \frac{1}{2} \right)^2 = \frac{1}{12}
\]
平均 \(\mu\)(= \(\avg{x}\))は分布の中心 1/2 で、
標準偏差 \(\sigma\) は \(\sqrt{1/12}\) = 0.288675... になります。
分布が ± 0.5 に広がっているからといって、標準偏差が 0.5 にはならないことに注意してください。
この [0, 1) 区間の一様分布を [a, b) 区間の一様分布に拡張するには、
\(y = a + (b-a)x\) という変換を施せばよいのです:
\[
f_y(y) = \left\{
\begin{array}{cl}
1/(b-a) & a \le y < b\\
0 & \mbox{その他}
\end{array}
\right.
\]
一般のモーメントの計算はこの分布関数を用いるのが簡単です:
\[
\avg{y^n} = \int_a^b y^n \rmd y = \frac{1}{n+1} \frac{b^{n+1} - a^{n+1}}{b-a} = \frac{1}{n+1} \sum_{i=0}^{n} {a^i b^{n-i}}
\]
分散は [0,1) 区間の一様分布 \(x\) の結果を用いた方が簡単です:
\[
\var{y^2} = \var{(a + (b-a)x)^2} = (b-a)^2 \var{x^2} = \frac{(b-a)^2}{12}
\]
前のページへ 次のページへ
「確率と統計のはなし」の表紙へ


