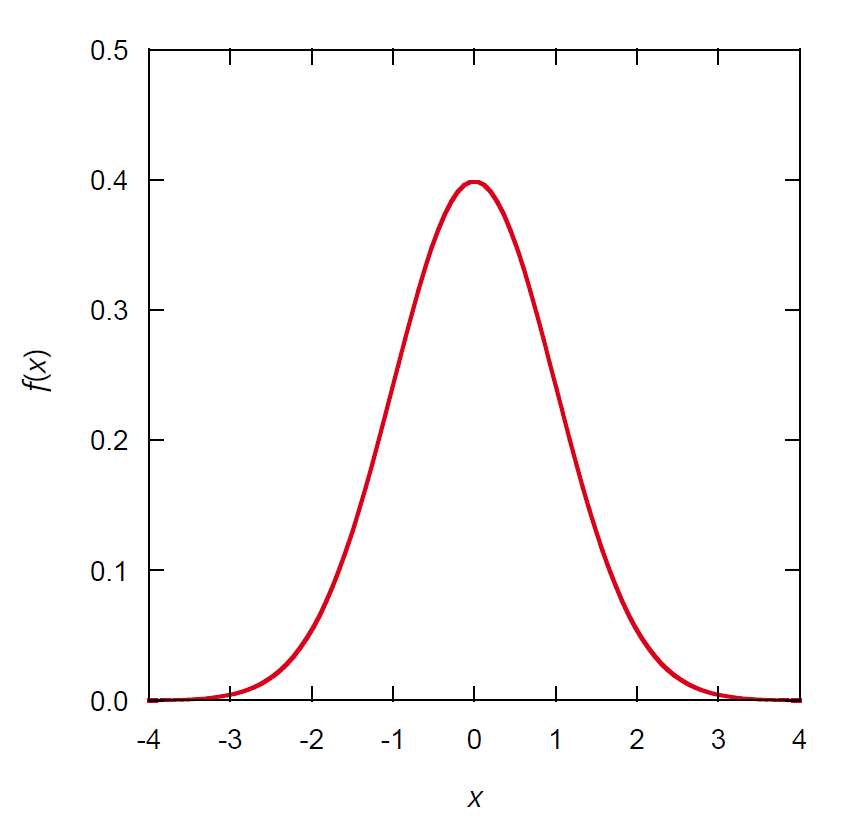
平均 \(\mu\)、分散 \(\sigma^2\) の正規分布(ガウス分布)は \(\mrm{N}(\mu,\sigma^2)\)と表記され、 分布関数は次式で与えられる。
\begin{equation} f(x) = \frac{1}{\sqrt{2 \pi} \sigma} \rme^{-\frac{(x - \mu)^2}{2 \sigma^2}} \label{eq:gauss1} \end{equation}
\(x\) について
\begin{equation} y = \frac{x - \mu}{\sigma} \label{eq:gauss2} \end{equation}
という変換を施すと、\(y\) は平均 0、分散 1 の正規分布 N(0, 1)に従うことになる。
\begin{equation} f(y) = \frac{1}{\sqrt{2 \pi}} \rme^{-\frac{y^2}{2}} \label{eq:gauss3} \end{equation}
これを標準正規分布 standard normal distribution と呼び、標準正規分布に従うランダム変数を標準正規変数と呼ぶ。

|

|
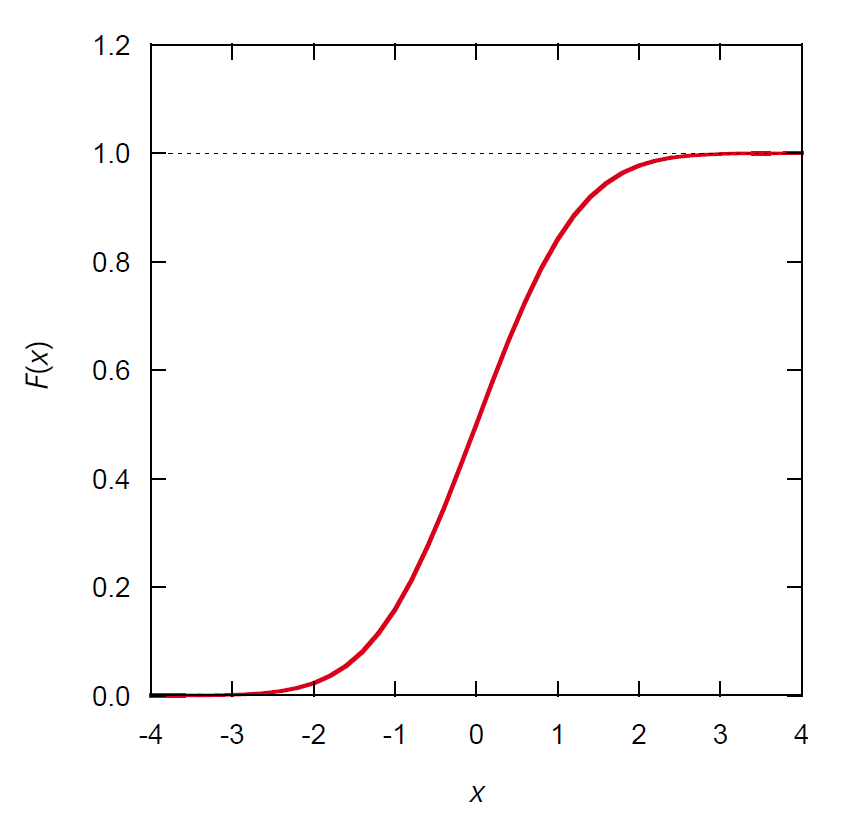
| 図 1a. 標準正規分布 N(0, 1) の分布関数。 | 図 1b. 標準正規分布 N(0, 1) の積算確率分布。 |
正規分布の重要な特徴は、正規分布に従う独立なランダム変数の和も正規分布に従うことである。 実際に 2 個の独立な標準正規変数の和 \(z = x + y\) の分布関数を計算すると次のようになり
\begin{equation} f(z) = \int_{-\infty}^{\infty} {f(z - y) f(y) \rmd y} = \frac{1}{2 \pi} \int_{-\infty}^{\infty} {\rme^{-\frac{1}{2}[(z - y)^2 + y^2]} \rmd y} = \frac{1}{2 \pi} \rme^{-\frac{z^2}{4}} \int_{-\infty}^{\infty} \rme^{- (y - z/2)^2} \rmd y = \frac{1}{2 \sqrt{\pi}} \rme^{-\frac{z^2}{4}} \label{eq:gauss4} \end{equation}
独立な標準正規変数の和が N(0, 2) の正規分布に従うことが分かる。 一般の正規分布についても、先の式 \eqref{eq:gauss2} の逆変換を取れば、\(\mrm{N}(\mu_1, \sigma_1^2)\) と \(\mrm{N}(\mu_2, \sigma_2^2)\) のランダム変数の和が \(\mrm{N}(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)\) の正規分布に従うことになる。
多数の独立なランダム変数 \(x_i\)(\(i = 1, 2, \cdots, N\))を加えたランダム変数 \(y = \sum_i x_i\) の確率分布は、たいてい平均 \(\sum_i \avg{x_i}\)、分散 \(\sum_i \var{x_i^2}\) の正規分布に近づくことが知られている (中心極限定理 central limit theorem)。 同じような分布関数に従うランダム変数の場合、典型的には5個程度の和を取るとほぼ正規分布と見なせるようになる。 測定値のばらつきは多くの独立な不確定要素が絡み合って生じることが多く、分布関数はたいていの場合、正規分布に従うものと考えてよい。 このため正規分布、そしてそれを決める要素である平均と分散に大きな注目が集まることにもなる。
中心極限定理が成り立つかどうか、 先の [0, 1) 区間の一様分布関数を用いてテストしてみましょう。
独立で同一の分布関数 \(f(x)\) に従う \(n\) 個のランダム変数 \(x_1, x_2, \ldots\, x_n\) の和 \(y = x_1 + \cdots + x_n\) を考えると、 その分布関数は、次の畳み込み積分になります:
\[ f_y(y) = \int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} [ f(y - x_2) f(x_2 - x_3) \cdots f(x_{n-1} - x_n) f(x_n) ] \rmd x_2 \cdots \rmd x_n \]
|
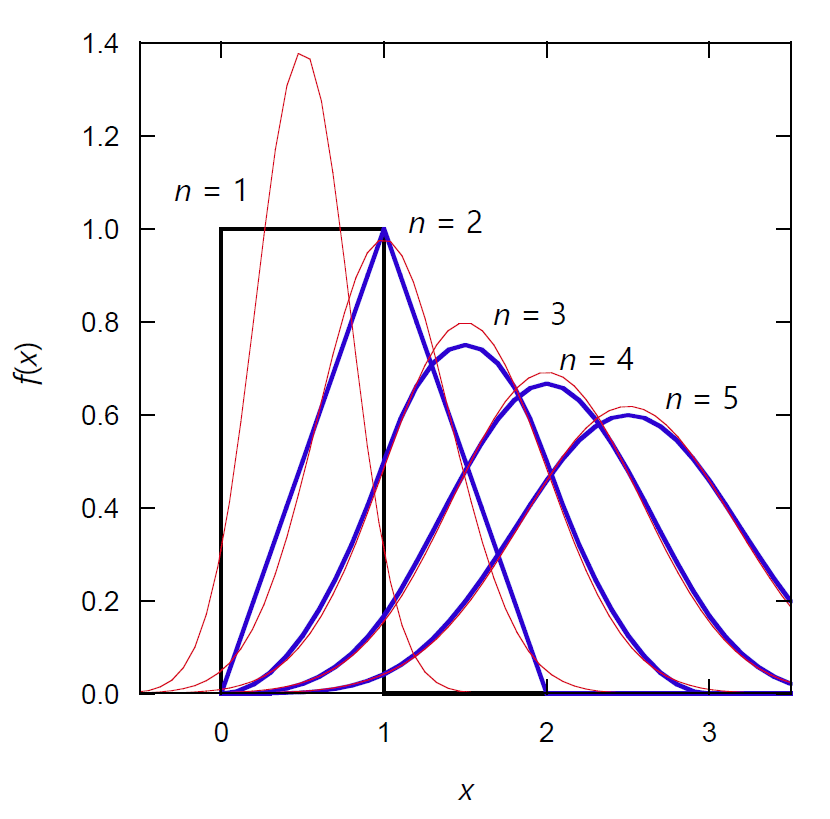
ここで \(f(x)\) として [0, 1) 区間の一様分布関数を取ると、 \(y\) の分布関数として次式を得ます(ラプラス変換を使うと簡単):
\[ f_y(y) = \sum_{i=0}^n \left[(-1)^i {}_n \mrm{C}_ i \frac{(y - i)^{n-1}}{(n-1)!} U(y - i) \right] \]
ここで \(U(x)\) は単位関数(階段関数)です。 図には \(n\) = 5 まで計算した結果を示しました。 図中、対応する平均と分散を持つ正規分布 N(\(n/2\), \(n/12\)) も示しています。 最初の箱型の分布関数が、畳み込み積分を順次行うにつれ、 正規分布に近づいていきます。
概形が似かよって来るように見えるのはよいのですが、少し定量的に比較するのに、 モーメントの計算を示しましょう。 表 1 には [0, 1) 区間の一様分布に従う独立な \(n\) 個のランダム変数を足しこんだランダム変数 \(y\) の分布関数 \(f_y(y)\) について計算したモーメント(表中 H の列)と、 それと同じ平均と分散を持つ正規分布 N(n/2, n/12) について計算したモーメント(表中 G の列)を示しました。 1 次と 2 次のモーメントは平均と分散が等しくなるようにとっているので当然同じになりますが、 一様分布の場合には平均値周りに対称な分布なので 3 次のモーメントも等しくなります (\(\avg{(x - \mu_1)^3}\) = 0)。 ですから両者の差については、4 次以上のモーメントに注目する必要があります。
4 次のモーメント μ4についてみると、n = 1 では一様分布と正規分布の比 H/G は 0.96 ですが、n = 2, 3, … と増えるにしたがって 0.992, 0.9971... , 0.9986..., 0.9992... と着実に 1 に近づいていきます。 5 次についても同様、0.8888..., 0.9729..., 0.9892..., 0.9946..., 0.9969... となっています。 このようにモーメントに注目することで、 足しこむ数が増えるにしたがって正規分布に近づくことが分かります。 しかしその近づき方はゆっくりしていて、 特に低確率の領域が正規分布に従うかどうかについては慎重に検討する必要があります (独立な [0, 1) の一様分布を n 個足しこんだ値域はあくまで [0, n) であって、 正規分布の期待する (-∞, ∞) ではありません)。
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H | G | H | G | H | G | H | G | H | G | |
| μ1 | 1/2 | 1/2 | 1 | 1 | 3/2 | 3/2 | 2 | 2 | 5/2 | 5/2 |
| μ2 | 1/3 | 1/3 | 7/6 | 7/6 | 5/2 | 5/2 | 13/3 | 13/3 | 20/3 | 20/3 |
| μ3 | 1/4 | 1/4 | 3/2 | 3/2 | 9/2 | 9/2 | 10 | 10 | 75/4 | 75/4 |
| μ4 | 1/5 | 5/24 | 31/15 | 25/12 | 43/5 | 69/8 | 243/10 | 73/3 | 331/6 | 1325/24 |
| μ5 | 1/6 | 3/16 | 3 | 37/12 | 69/4 | 279/16 | 185/3 | 62 | 675/4 | 8125/48 |
なおランダム変数の和ではなく積が同じ分布に従う分布として、正規分布に従うランダム変数 \(x\) を指数に持つ \(y = \exp(x)\) というランダム変数を考えることができます。 このランダム変数は対数正規分布 log normal distribution と呼ばれる分布に従い、 粉粒体のサイズ分布などでしばしば見られます。