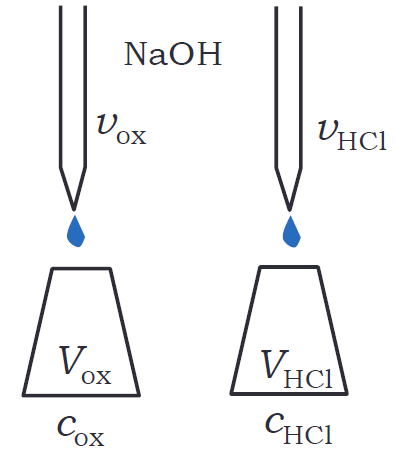
|
| 図 3-1．標定と試料の滴定操作 |
標準溶液の調製に関わって、 1/1000 の精確さを実現する話をみたわけですが、 その後の実験操作を考えると無駄な努力のようにも見えます。 たとえばホールピペット（全量ピペット）の許容誤差は、 JIS R3505 では 10 mL で ±0.02 mL ということになっていて、 1/1000 に届きません。 では標準溶液にかけた努力は無駄だったんでしょうか？ そうではありません。 実験を巧妙に設計することで、 1/1000 が視野に入ってくるのです。
|
|
| 図 3-1．標定と試料の滴定操作 |
実験ではシュウ酸標準溶液（濃度 \(c_\mrm{ox}\)）をホールピペットで体積 \(V_\mrm{ox}\) とって水酸化ナトリウム溶液で滴定した後、 試料溶液である塩酸（濃度 \(c_\mrm{HCl}\)）をホールピペットで体積 \(V_\mrm{HCl}\) とって水酸化ナトリウム溶液で滴定します。 起きる反応はそれぞれ次のように書けます。
H2C2O4 + 2 NaOH → Na2C2O4 + 2 H2O
HCl + NaOH → NaCl + H2O
それぞれの滴定の滴定値を、\(v_\mrm{ox}\)、\(v_\mrm{HCl}\) とし、 水酸化ナトリウム溶液の濃度を\(c_\mrm{NaOH}\) とすると、 次式が成立します。
\[ c_\mrm{ox}~ V_\mrm{ox} = \frac{1}{2}c_\mrm{NaOH} ~v_\mrm{ox} \\ c_\mrm{HCl} ~V_\mrm{HCl} = c_\mrm{NaOH} ~v_\mrm{HCl} \]
したがって、試料である塩酸の濃度 \(c_\mrm{HCl}\) は標準溶液であるシュウ酸濃度 \(c_\mrm{ox}\)と、 次の関係にあります。
\begin{equation} c_\mrm{HCl} = \frac{V_\mrm{ox}}{V_\mrm{HCl}} \frac{v_\mrm{HCl}}{v_\mrm{ox}} 2 c_\mrm{ox} \label{eq:vanalX} \end{equation}
ここで考える滴定操作では、 フェノールフタレインを用い、目視で終点を判定します。 実験テキストなどであまり注意されることがないようですが、 変色が十分明瞭である時、指示薬を用い目視で終点を判定するなら、 一般に入れすぎてしまいます。
滴定操作で１滴 \(a\) ずつ加えていく過程を考えましょう。 滴定では変色を確認したところで滴定を止め、 そこまでに加えた量を滴定値とします。 ですから滴定値は、 真の滴定終点（変色点）より平均的に \(a/2\) 大きくなり、 またその分散としては、\(a^2/12\) （標準偏差は\(a/2 \sqrt{3}\)）が見込まれます。 学生実験で使用している通常の 25 mL 程度のビュレットから滴下する液滴は、特に操作しなければ 0.04 mL 程度のものですから、 滴定値には +0.02 ｍL の偏り（バイアス）と 0.012 mL 程度の標準偏差があることになります。
|
|
| 図 3-2. 目視で終点を判定すると入れすぎる。 偏りが \( (a/2) \pm (a/2)\) の範囲に均一に分布するなら、 分散は \(a^2/12\) になる。 | |
なお上では変色点と当量点が一致するものとしての扱っていますが、 一般に変色点と当量点は完全には一致せず、 使用する指示薬（たとえばフェノールフタレインとブロモフェノールブルー）によっても偏りが生じます。 また目視による終点の偏りの評価は、個人差もあり、一般に困難です。
滴定値に偏り（バイアス）が生じることを見たわけですが、 最初に触れたホールピペットの誤差といい、 1/1000 の精確さはとても望めないように思えます。 けれども標定操作を組み込むことで偏りは大きく低減されます。
ホールピペットの誤差も考慮した形で、 最終的に式 \eqref{eq:vanalX} から得られる塩酸の濃度 \(c_\mrm{HCl}\) の誤差を評価すると、 標準溶液の濃度の誤差 \(\Delta c_\mrm{ox}\) は無視できるものとして、 誤差の表現を求めると次式のようになります。
\begin{equation} \frac{\Delta c_\mrm{HCl}}{c_\mrm{HCl}} = \left [ \frac{\Delta V_\mrm{ox}}{V_\mrm{ox}} - \frac{\Delta V_\mrm{HCl}}{V_\mrm{HCl}} \right] + \left [ \frac{\Delta v_\mrm{HCl}}{v_\mrm{HCl}} - \frac{\Delta v_\mrm{ox}}{v_\mrm{ox}} \right] \label{eq:vanalY} \end{equation}
この式 \eqref{eq:vanalY} を見ると、 巧妙に塩酸の濃度 \(c_\mrm{HCl}\) の偏りが打ち消される構造になっていることが分かります。 まず右辺第１項の\([ ~~]\) に注目しましょう。 実験操作にはあからさまに記述されていませんが、 シュウ酸溶液と塩酸溶液をはかり取るのに、 面倒なようですが、 同一のホールピペットを共洗いして使っているはずです。 同じホールピペットを使っているのですから、 採取する溶液量 \(V_\mrm{ox}\)、 \(V_\mrm{HCl}\) の偏りは打ち消されます （ \( \langle \Delta V_\mrm{ox} \rangle = \langle \Delta V_\mrm{HCl} \rangle \) ）。 ホールピペットが何本もあって、 「シュウ酸用」「塩酸用」という風に使えば、 共洗いの必要がなくスムーズに実験が進められそうですが、 そうしたことをすると、採取する溶液量の偏りは打ち消されず、 測定値に偏りが生まれます。 ケチだからホールピペットを１本だけにしているわけではないのです！
次に右辺第２項の\([ ~~]\) を見てみましょう。 同じ指示薬を使っておれば滴定値の偏りはほぼ同じで（\( \langle \Delta v_\mrm{ox} \rangle \approx \langle \Delta v_\mrm{HCl} \rangle \)）、 滴定量がほぼ同程度であれば（\(v_\mrm{ox} \sim v_\mrm{HCl}\)。 通常、相違は 10 %程度でしょう）、 滴定値の偏りは打ち消されます。 たとえばシュウ酸溶液の調製をまちがえて、 濃度を２倍の 0.1 mol/L にしたとしましょう。 単純に考えると、標定の際の滴定値 \(v_\mrm{ox} \) が２倍になるだけで、 実験に支障はないように思えるかもしれません。 しかし滴定値の偏りに注意すると、 滴定値の間の偏りの打ち消しが起きなくなり、 結果に偏りを生じさせることになるので好ましくありません。
ここでは話を簡単にするため、 ビュレットの誤差を考慮していませんが、 ビュレットの目盛りが等間隔に付けられておれば、 式 \eqref{eq:vanalX} は、 ビュレットではかった体積の偏りが打ち消される構造になっています （\(v = k v^\circ\) であるとすると、\(v_\mrm{HCl}/v_\mrm{ox} = v^{\circ}_\mrm{HCl}/v^{\circ}_\mrm{ox}\) ）。
滴定値に偏り（バイアス）が生じることを見たわけですが、 式 \eqref{eq:vanalY} から得られる、偏差の分散を考えると、 \(V_\mrm{ox} = V_\mrm{HCl} = V\)、 \(v_\mrm{ox} \approx v_\mrm{HCl} = v\)、 \(\langle (\delta V_\mrm{ox})^2 \rangle = \langle (\delta V_\mrm{HCl})^2 \rangle = \langle (\delta V)^2 \rangle \)、 \(\langle (\delta v_\mrm{ox})^2 \rangle \approx \langle (\delta v_\mrm{HCl})^2 \rangle = \langle (\delta v)^2 \rangle \) として、次式のようになります。
\begin{equation} \frac{\langle \delta c_\mrm{HCl} \rangle^2}{c_\mrm{HCl}^2} \approx 2 \frac{\langle (\delta V)^2 \rangle }{V^2} + 2 \frac{\langle (\delta v)^2 \rangle }{v^2} \label{eq:vanalQ} \end{equation}
ここで右辺第１項のホールピペットの採取量の分散 \(\langle (\delta V)^2 \rangle\) は、 10 mL のホールピペットで、 少し練習すれば (5 μL)2 程度にはなります。 第２項は滴定終点の判定が鮮明であれば、終点近傍で加える１滴の体積 \(a\) にかかっていますが、 半滴 0.02 mL のオーダーまでにすれば、およそ \(\langle (\delta v)^2 \rangle \sim (a^2 / 12) \approx \) (6 μL)2 といったところです。 ですから、えられる塩酸濃度の分散の相対値 \(\langle (\delta c_\mrm{HCl})^2 \rangle / c_\mrm{HCl}^2\) は (1.1 × 10-3)2。 つまり少し手練を積めば、 標準偏差は 1/1000 のオーダーには届くわけです。