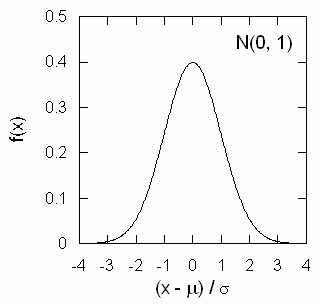
図2.標準正規分布のグラフ
1章では何らかの実験で得られた N 個のデータの平均 μ、分散 σ2、標準偏差 σ の大雑把な意味合いや計算について述べました。 実験で得られたデータの平均や分散(標本平均、標本分散)を計算する時、 実験の背景にある無数のデータの集団(母集団)の平均や分散を推定するという立場に立ってデータを取り扱います (標準偏差を計算する時、データ数 - 1で割る)。 ここではもっと単純化して、 無数のデータの集団について、あるデータ x の出現確率 Pr(x) がよく分かっているという前提の下で、 平均、分散などの統計量について、見てみることにしましょう。
ある量を測定し x というデータを得るものとし、x の関数 q(x) についてその平均を <q(x)> で表記することにします。 ここで平均を次式で定義します。
この記法を使うと、平均μ、分散σ2 は、それぞれ次のように定義されます。
また分散は次のように、2乗の平均から平均の2乗を引いたものとしても記述できます。 (この文脈では平均・標準偏差はただの数であって確率変数でないことに注意)
かりに q = a x + b という1次関数を考えると、q の平均μq、分散 σq2 は、 x の平均、標準偏差と次の関係にあります。
σq2 = a2 σ2、 σq = | a | σ
すでに述べたように平均は x のおよその値を与え、分散(標準偏差)は x の値が平均値からどれぐらいばらけているかの度合いを与えてくれます。 次のチェビシェフの不等式は、この平均と分散(標準偏差)の関係を如実に示すものです。
チェビシェフの不等式によると、平均値の周りに標準偏差σの 2 倍ぐらいの幅を取れば、最低、全体の4分の3はカバーできます。 チェビシェフの不等式は統計分布によらず成立するわけですが、 個々の統計分布の特性を取り込むことで、もっと強い条件を導くことができます。 たとえば図1の玄米の重さの分布では、平均値の周り、±σ の範囲でだいたい4分の3ぐらい入っていました。

出現確率 Pr(x) が x に対してどのような変化を示すかについては、2項分布を始めさまざまな分布が知られていますが、 後でも述べるように特に重要なのは正規分布(ガウス分布)です。 正規分布は連続関数で与えられ、ある値 x 近傍のデータの出現する確率密度 f(x) は次式で表されます。
ここで C は規格化のための定数です(C2 = 1/2πσ2)。 正規分布の特性は平均値と分散が与えられると決まり、一般の正規分布は N(μ, σ) のように表記されます。 そして一般の正規分布に従う変数 x に次のような変換をほどこす事で、 平均 0、標準偏差 1 の正規分布(標準正規分布)に従う変数 q に焼き直すことができます。
こうした操作を「標準化」と称し、図2に示すのは標準正規分布です。 正規分布(ガウス分布)は釣鐘型の分布を示し、チェビシェフの不等式よりもっと強い以下のような関係式が成立します:
ここでは統計分布の特色を、平均 <x> と分散 <x2> - <x>2 で見たわけですが、 <x3>、<x4> といった高次のべき乗の平均(「モーメント」と称します)に注目することで、 もっと統計分布の特色を語ることができるはずです。 こうした考え方は確率 P(x) のフーリエ級数展開に通じます(x = exp(ik) と置き換えてみてください)。 しかし実用的に重要な確率分布(特に正規分布)は2次までのモーメントで決まってしまうので、あまり表に出ることはないようです。