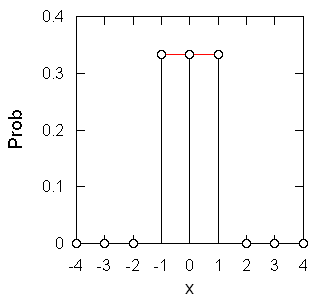
図3a. 1個の確率変数 x = x1 の確率分布
x = x1 + x2
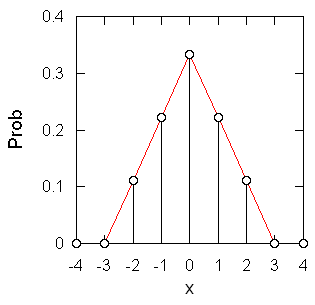
図3b. 2個の確率変数の和 x = x1 + x2 の確率分布。
x = x1 + x2 + x3
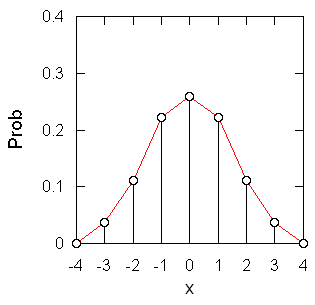
図3c. 3個の確率変数の和 x = x1 + x2 + x3 の確率分布。
いくつかの測定値の平均や分散を問題にする際、それぞれの測定はその前後の測定と関わりなく行われるのが普通です。 こうした「独立」の測定値の和や差の不確かさについては、「加減した数の分散は、加減する数の分散の和になるという性質があります。
独立に行われた測定値 x、y の和を z とします。
この時、z の平均、分散は、x、y の平均・分散を用いて次式のように表現できます。
ここで x' = x - μx、y' = y - μy とおきました(<x'> = <y'> = 0)。 x と y は独立なので、<x' y'> = <x'> <y'> = 0 となります。
ポイントは、z の標準偏差が x、y それぞれの標準偏差の和よりは小さいことです。 たとえば標準偏差を用いて誤差を見積もったとすると、±0.1 のデータを足したものの誤差は、±0.2 ではなく、±0.141 ... となるのです。 このような挙動はちょっと意外に思われるかもしれません。 ±0.1 のデータを足せば、±0.2 になるはず・・・。
簡単のため、-1、0、+1 となる確率が等しく 1/3 であるような変数、{xi} を考えて、その和を考えてみましょう。 2変数の和 x1 + x2 を取ると図3b に見るような値域が -2 から +2 に広がった分布を得ます。 しかしその確率分布は一様ではなく、中心に偏った形になっています (たとえば x = 2 になるのは (x1, x2) = (1, 1) の場合だけなのに対し、x = 0 となるのは (-1, 1), (0, 0), (1, -1) という3つの場合であることなどに注意)。 値域は広がるのですが、分布が平均値の周りに収縮する結果、標準偏差は2倍ではなくルート2倍、1.414... 倍になるのです。 同様にもう一つ、3つの和を取ると図 3c のような確率分布に従い、釣鐘型の形状を持つようになります。 こうして多くの独立な確率変数を足しこんだものは (例外はありますが)最終的に正規分布に接近していきます(中心極限定理)。

図3a. 1個の確率変数 x = x1 の確率分布 |
⇒ ⇒ ⇒
x = x1 + x2 |

図3b. 2個の確率変数の和 x = x1 + x2 の確率分布。 |
⇒ ⇒ ⇒
x = x1 + x2 + x3 |

図3c. 3個の確率変数の和 x = x1 + x2 + x3 の確率分布。 |
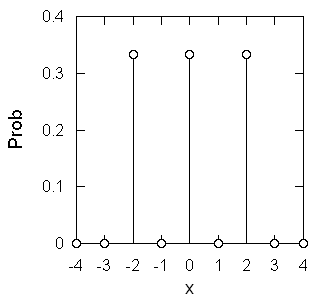
なおここでは、独立な変数の和を考えていたことは重要です。 もし x = x1 + x1 (= 2 x1) という変数を考えるなら、その分布は図3d のようなものになるだけで、一様な分布の形状に変化はおきません。
有効数字の計算で、足し算・引き算で「最後のケタを揃えて計算する」ことの根拠も、独立な値の和・差の分散が、元の数の分散の和になっていることにあります。 たとえば 2.56 + 3.3 という計算を取れば、2.56 について分散は最大 0.12 = 0.01、3.3 については 12 = 1 ですから、 2つを足した結果の分散は 1 だと見なせます。つまり結果は 5.9 というわけです。 同様に10回測っていずれも 3.12 というデータがえられたとすれば、その平均値は 3.120 と、1ケタ上げて記載することが妥当であるということになります。
最後に正規分布に従う確率変数について触れておくと、 通常の実験では、多くのふらつきを生み出す要素が最終結果に独立に関わっています。 ですから実験データの偏差が正規分布に従うと考えても、そんなに見当違いではありません。 特に5個ぐらいのデータの平均(5個の独立な変数の和)の分布は、正規分布に従うと見なしてよい理論的な根拠(中心極限定理)が存在しています。 正規分布が統計理論において重要な位置を占めるのはこうした背景があるためです。