|
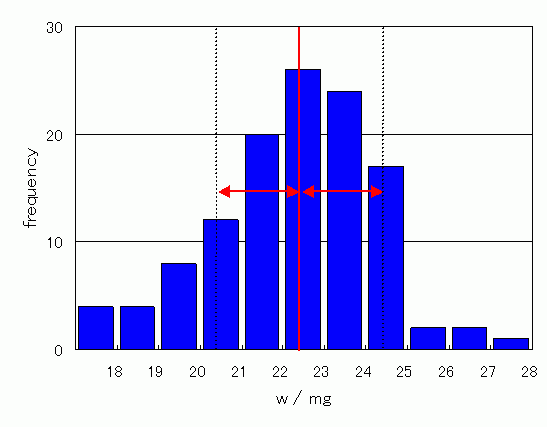
図1. 玄米(福島産コシヒカリ)1粒の重さの分布(2003年度学生実験の結果から)。 平均 μ = 22.31 mg、標準偏差 σ = 2.02 mg。 縦の赤い実線は平均 μ、黒い点線は μ ±σ の位置を示す。 |
何らかの実験で得られた N 個のデータ {xi} があるとしましょう。 実験データにはさまざまな原因でゆらぎが現れ、得られたデータはある分布を持ちます。 この分布の特色をいくつかの特性値に凝縮することが一般に行われます。 この時よく用いられる特性値として、平均 μ、分散 σ2、標準偏差 σ があります。
平均 μ は皆さんよくご存知のように、データの総和をデータ数で割って計算されます。
分散 σ2、標準偏差 σ については、なじみのない人がいるかもしれません。 まず偏差2乗和(偏差平方和、残差2乗和) S を次式で定義します。
分散 σ2 は偏差2乗和を、データの総数 N から 1 を引いたもので割ったもので、 標準偏差 σ は分散の平方根をとったものです。
平均は x のおよその値を与え、分散(標準偏差)は x の値が平均値からどれぐらいばらけているかの度合いを与えてくれます。 図に 120 粒の玄米を一粒ずつ 0.1 mg まで精確に量った結果の頻度分布を示します(2003年度の学生実験の結果の一部です)。 米粒の重さはだいたい 19 mg から 25 mg の間にあり、少し軽い側に分布がずれた釣鐘型になっています。 この分布から計算される平均は 22.31 mg、標準偏差は 2.02 mg でした。 図の縦の赤い実線が平均値の位置、両向き矢印は標準偏差に対応する長さを示しています。 平均値が分布の中心位置、標準偏差が大まかな分布の広がりの目安を与えてくれていることがわかります。 この例では平均値の周り±σ の範囲に全体の 72 %、87 粒のデータが収まっています。

|
図1. 玄米(福島産コシヒカリ)1粒の重さの分布(2003年度学生実験の結果から)。 平均 μ = 22.31 mg、標準偏差 σ = 2.02 mg。 縦の赤い実線は平均 μ、黒い点線は μ ±σ の位置を示す。 |
ここでよく混乱が起きるのは分散・標準偏差の計算です。 偏差2乗和をデータ数 N で割ってしまいたくなるからです。 しかし化学実験の課題で標準偏差を使うときは、この定義で計算したもの (「標本分散」「標本標準偏差」とも呼ばれます)を使ってください。 カシオの統計機能付きの電卓を持っている人であれば、 「σn」ではなく「σn-1」という方の結果を使って欲しいのです。
なぜ N - 1 で割るかについては、また後で述べますが、 得られたデータの不確かさ(直接的には平均値 μ の不確かさ)を考慮した結果であると考えていただけたらよいと思います。 同じ条件で同じように測定を行って N 個のデータを得た無数の自分のクローン(複製)を思い浮かべてみてください。 今手にしている N 個のデータは、あり得たであろう無数の結果の一つで、 ここでは、手にしたデータから、無数のデータの平均なり標準偏差なりを推し量ろうとしているのです (先に述べた「平均値の平均値」や「分散の平均」を考えようとしているわけです)。 実際、1個しかデータがなければ、データのばらつきなんて見当のつけようもありません。
この点で中学・高校時代に皆さんが出会ったであろう「偏差値」での標準偏差の扱いは、毛色が違っています。 ある人の成績の偏差値 di は、その人のテストの点数 xi から、 試験成績の平均点 μ、標準偏差 σ を用いて次のような計算式で定義されています。
ここで使われる標準偏差 σ は、偏差2乗和を人数 N で割ったもの S/N、の平方根です。 偏差値を考える時には、対象とする集団がすでに完全にわかっています。 ですから「平均値の平均値」や「標準偏差の平均」を議論する余地はなく、与えられた集団の中で閉じた議論でよいのです。
化学実験で扱う数値データの場合には、そもそものどんな分布に従うデータが出てくるか分かっていません (分かっていればやる必要がないとも言える)。 偏差値の例で言うと、かりに 10000 人の受験者のいる試験があったとしましょう。 この時、その試験を受験したある学校の生徒 100 人の成績だけから偏差値を計算するようなものです。 偏差値の計算には 10000 人の平均点、標準偏差が必要なわけですが、 それを 100 人分の平均点、標準偏差で置き換えるとしたらどうするのがいいでしょう? 化学実験の数値データの取り扱いは、いわばこの学校がきわめて「平均的」な学校であるとして、 10000 人の平均点、標準偏差の、「平均的」に正しい評価法を問題にしていると考えていただければ結構です。
ここで問題にする「平均」は、上式に示すようにいわゆる算術平均に相当するものです。 これ以外にも、幾何平均(正の値を取るデータ N 個を掛け合わせて、その N 乗根を取る。 平均律の音階では幾何平均が有用。ドとミの周波数の幾何平均がレの周波数)、 調和平均(逆数の算術平均を取り、その逆数を取ったもの。 ピタゴラス音階の構成法の基調にある)といったものも登場することがあります。