|
|
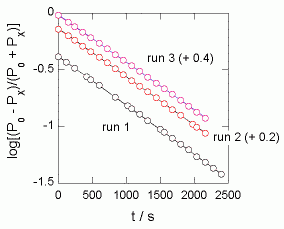
| 図4-1 開放型装置での実験例 | 図4-2 閉鎖型装置での実験例 |
図4-1 に予備実験で行った開放型についての実験結果を示します。 室温は 27℃、使ったステンレスチューブは内径 0.23 mmのものでした。 3回やった結果はよく一致しています。 粘度が圧力に依存しないとして導いた式がきれいに成立していることがわかります。 気体分子運動論の教えるとおり、空気の粘度は圧力に依存しなかったわけです。

|

|
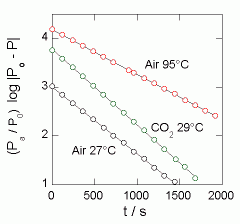
| 図4-1 開放型装置での実験例 | 図4-2 閉鎖型装置での実験例 |
図4-1 の直線の勾配から、少し定量的な空気の粘度の導出を行ってみます。 3回実験を行って得られた b の値は (9.7±0.1)×10-9 Pa-1 s-1。 フラスコの体積を 500 mL、チューブの長さを 1 m、チューブの半径を 0.115 mm として空気の粘度を計算すると、14 μPa s という結果を得ます。これは 27℃での空気の粘度として知られている 18.6 μPa s と比較すると 25% ぐらい小さい数字になっています。 この不一致はフラスコの体積が死容積の部分も含めて 700 mLぐらいだったとして説明がつきます。
もっともこの実験から空気の粘度の絶対値を決定するのはチューブの内径の誤差の問題があって、そもそも精度が期待できません。 カタログ記載のステンレスチューブの内径の公差は±0.02 mm、±9% 程度ですが、b の値には半径の4乗で効くので、40%ぐらいの誤差は覚悟しなければならないからです。
図4-2 には、閉鎖型装置で室温で空気についての実験結果、チューブを沸騰水中に浸けた空気についての結果、二酸化炭素での結果を示しました。 比較を容易にするために、縦軸は式 (3-11) の左辺に大気圧 Pa と最終到達圧力 P0 の比をかけたもので表わしています。 図からただちに空気より二酸化炭素のほうが粘度が小さいことがわかります。 また空気について温度を上げた場合の勾配の比が 0.67 と、温度の比(300 K/368 K)の 0.82 より小さいことから、粘度が大きくなることもわかります。