３．結果の解析

細管の中のおそい流体の流れはポアジュイユ（Poiseuille）の流れとして知られ、ハーゲン（Hagen）－ポアジュイユの法則を用いて記述することができます。この法則によれば定常状態における流体の流れは次の式で記述できます。

　　(3-1)

ここで η は粘度、a は管の半径、Ｇ は圧力の勾配です。 この法則が成り立つにはレイノルズ数が十分小さいことが必要ですが、今回の実験条件ではレイノルズ数は 100 以下でこの要件を満たしています。 また平均自由行程が十分短いことも必要な条件ですが、これも 1 μm以下で問題ありません（というかこうした条件を満たし、かつ１時間以内で１つの測定が終わるようにチューブを選択したのです）。

この式を液体の流れに適用する際には流体の圧縮性を考慮する必要はありませんが、気体の流れにこの式を適用する時には、気体の収縮・膨張の効果を正しく評価しておく必要があります。 気体の流れを取り扱う場合には、流れが定常状態になったとしても流れの速さは細管の場所場所で異なっています。言いかえれば圧力勾配が一定ではありません。この問題を定量的に議論するには、定常状態で質量の流れ・粒子数の流れが一定であることに注目します。 そしてここがポイントですが、粘度が圧力に依存しないとします。つまり以下の導出で出てくる関係が、実験的に再現できないなら、粘度は圧力に依存して変化するということになるわけです。

下の図のように座標をとり、Y から X 方向への流れを正にとるものとしましょう。

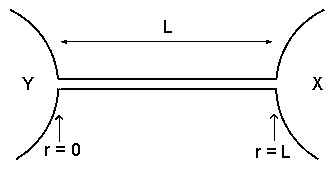
まず定常状態での粒子数の流れを c とすると、理想気体の状態方程式から r における流れの速さ u(r) は c と次の関係にあります。

　　(3-2)

ここで k_B はボルツマン定数、T は温度、P(r) は r における圧力です。したがって細管の内部の圧力の分布は(１)式を用いて次の微分方程式で表現できることになります。

　　(3-3)

この微分方程式をといて、質量の流れ c を細管の長さ L、細管両端の圧力 P_Y 、P_X を用いて表わすと次のような関係を得ることができます。

　　(3-4)

容器 X の圧力変化は、容器の体積を V_X とすると気体の状態方程式から次のように表わされます。

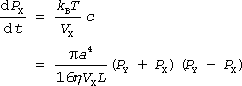　　(3-5)

開放型の場合には、P_Y = P_a （大気圧）で一定ですから、次の関係式を得ます。

　　(3-6)

装置による定数 b

　　(3-7)

を導入し、積分形で書くと次の関係式になります。

　　(3-8)

ここで閉鎖型の場合について考えましょう。もし２つの容器の体積が等しければ、閉鎖型では P_Y + P_X は一定で、最終の圧力 P₀ の２倍に等しいはずです。 ですから次の関係式が成り立ちます：

　　(3-9)

したがって閉鎖型についての微分方程式は次のようになります。

　　(3-10)

開放型と同様に積分形の式を書くと

　　(3-11)

この導出で２つのフラスコの体積は等しいと置きましたが、もしフラスコの体積が等しくないときには式はもう少し複雑になります。V_X/V_Y = 1 + 2α とおくと

　　(3-12)

積分形では

　　(3-13)

です。十分 α が小さければこれは

　　(3-14)

としたのと同じことです（あるいは(3-12)式で P₀ - P_X の２次項を無視して線形化したことに相当）。

なお温度を変えた実験の場合には、上の扱いで、容器の温度と細管の温度とが等しいとしている前提が成立せず、実測される b* は温度の比だけ変化します。

　　(3-15)

ここで T_r は室温です。