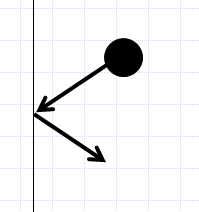
図3-1. 平らな剛体壁面に衝突する分子。 直接壁面に衝突する分子について、衝突する際の運動量変化を評価することで、圧力を知ることができる。
前章では分子の配置について考え、 それが熱力学量とどう関わるかについて見ました。 ここでは「力」という面から、液体を考えてみることにしましょう。
まず気体分子運動論で皆さんよく御存じと思いますが、 流体の圧力というのは、 分子間力そのものではないという何でもない事実に注目ください。 教科書を見ると分子間相互作用として、 静電相互作用や水素結合、分散力、交換斥力といったものがいろいろ並んでいますが、 いろんな分子間力が働いたところで、 われわれが流体の圧力として測るものは、 器壁と流体を構成する分子の間に働く力です。 器壁と流体分子の間の相互作用についても、いろいろ言うべきことは多いのですが、 ここでは話を単純にして、 前章同様、パチンコ玉からできた流体と、 剛体的な相互作用するをする壁を考えることにします。

P = ρT (3-1)
ここでρは分子の数密度で、単位体積中の分子数です。*1 この状態方程式の導出については、 すでに皆さん学ばれたことと思います。 ではこの論法は液体について成り立つのでしょうか? もし成り立つなら、すべての液体は理想気体として振る舞うことになります。 学部レベルの物理化学の教科書では、 このあたりの事情について語られず 「気体は気体、液体は液体」 といった記述に終始しているようです。 でも2章で触れたように、 マクスウェルの速度分布則は通常の液体でも成立しますし、 式の導出に問題はありません。 ではどこに問題があるのでしょうか?
P = ρC T (3-2)
十分希薄な状態では、 どこをとっても密度は一定とみなせるので、 接触距離の密度ρC は流体の密度(バルクの密度)ρと同じとみなせ、 理想気体の状態方程式が成立します。 しかし密度を上げていくと、 器壁との接触距離における局所的な密度は複雑に変動します。 例えば前章の図2-4を思い出してもらえば、 パチンコ玉からできた流体では器壁の密度は流体の密度より大きく、 理想気体の状態方程式で想定されるより大きな圧力を示します。 あるいはその変動を、 われわれはある流体の状態方程式として観測しているといってもよいのです。
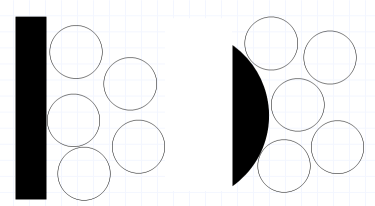
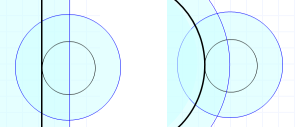
上では平らな壁面について考えましたが、 器壁の形状によっても粒子分布は変化し、 図3-2 のような直線状の壁面と弧状の壁面でも、 接触距離の密度は違ってきます。 このことは排除領域の大きさを考えると、 ある程度察しはつきます。 壁面に接したパチンコ玉の配置を考えると、 凸型の壁面の方がパチンコ玉の排除領域との重なりが小さく、 存在確率が小さくなることが期待されるからです。
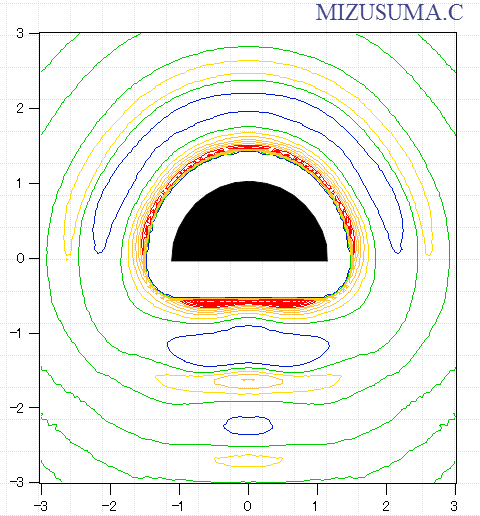
先の議論をさらに進めれば、 分子の表面についても、同様のことを考えることができます。 分子の形状が複雑になると、 分子各部にかかる圧力は均一ではなくなるのです。 図3-3 に示すのは半月盆状の分子の周りのパチンコ玉の分布です。 円弧の部分に比べて、 弦の部分の中心部では接触距離の密度が高く、 大きな圧力がかかっています。 また半月盆の尖った部分の周りでは、 密度が低くて受ける圧力も小さくなります。 分子レベルで見たとき、 パスカルの原理は成り立ちません。
ΔV = (∂PX/∂P)ΔVX (3-3)
ここでPX は、分子コアを変化させる部位に働く圧力です。 分子の注目する部位に及ぼされる圧力 PX と、系の圧力 P の関係が分かっていないと、 体積変化の正しい評価はできません。 たとえば分子の部位によっては、流体の圧力 P の増加とともに、 及ぼされる圧力が低下することもありえます。 この場合、分子コアを大きくすることで、体積の減少が起きることになります。