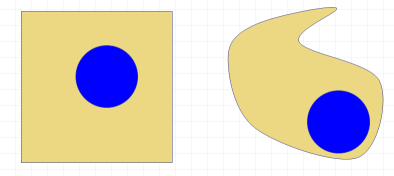
 図2-1. パチンコ玉の存在確率。
1個しかないときには、領域内のどこをとっても等確率。
図2-1. パチンコ玉の存在確率。
1個しかないときには、領域内のどこをとっても等確率。
平衡状態の速度分布の場合には、各分子の速度分布は独立で、 ある分子が上向きに運動しているからといって、 周りの分子の速度の向きはそれと無関係です。*1 けれども速度と違って、容器中のある場所に、分子がどれくらいの確率で存在するかは、 他の分子がどこに存在しているかに依存していて、 単純ではありません。 これは分子間の相互作用エネルギーが分子配置に依存しているためです。 分子間相互作用に関わってはいろいろ考えないといけないことが多いのですが、 話を簡単にするために、以下では一辺の長さ L の正方形の箱の中に入ったパチンコ玉の分布を考えます。 パチンコ玉の中心はこの箱の外に出られず、 パチンコ玉同士は距離1(パチンコ玉の直径を長さの単位にとったことに相当)以内には近づけないものとします (=剛体的な相互作用のみからなる系)。*2
 図2-1. パチンコ玉の存在確率。
1個しかないときには、領域内のどこをとっても等確率。
図2-1. パチンコ玉の存在確率。
1個しかないときには、領域内のどこをとっても等確率。
古典統計力学における重要な原理は、 箱の中にパチンコ玉が1個しかない時、箱の中の粒子分布は均一とみなせるということです。 これは当たり前のように思われがちですが、 たとえば図2-1のような複雑な形状の箱を考えて見てください。 先の尖がったところと、箱の中央とでは、粒子の存在確率が違ってもよいように思えませんか? こんな場合でも、どの場所をとっても存在確率が等しいとするところから、 液体の統計力学の話が始まります。
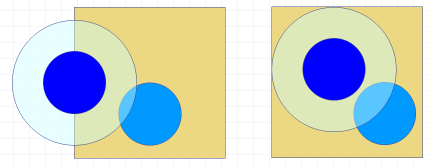 図2-2. 2個のパチンコ玉の存在確率。
2個目のパチンコ玉(水色)が存在できる領域の面積(自由体積)は、
最初の1個が正方形の辺上にある時(L2 - (π/8))の方が、
正方形の中心近くにある時(L2 - (π/4))より大きい。
パチンコ玉は正方形の中央付近より、辺上により多く見出されることになる。
図2-2. 2個のパチンコ玉の存在確率。
2個目のパチンコ玉(水色)が存在できる領域の面積(自由体積)は、
最初の1個が正方形の辺上にある時(L2 - (π/8))の方が、
正方形の中心近くにある時(L2 - (π/4))より大きい。
パチンコ玉は正方形の中央付近より、辺上により多く見出されることになる。
P2(R1, R2) = P1(R1) × P1(R2; R1)ここで P1(R1)は、R1によらず一定ですが、P1(R2; R1)は、 R1によって値が異なります。 図に示すように、R1が正方形の頂点である場合は、R1が正方形の中心の場合に比べて、 より確率が高くなります。 2個のパチンコ玉を考えると、 その内1個が正方形の境界線付近に存在して、排除領域が小さくなると、 その分統計的な重みが大きくなる、 つまり正方形の境界線近傍でパチンコ玉を見出す確率が高まるのです。
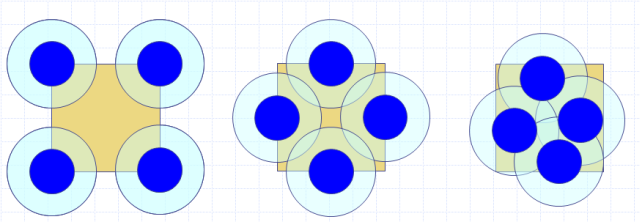 図2-3. 多数のパチンコ玉が存在する場合の存在可能領域。
5番目のパチンコ玉の存在できる領域の面積は、
4個のパチンコ玉の配置によって、複雑に変化する。
図2-3. 多数のパチンコ玉が存在する場合の存在可能領域。
5番目のパチンコ玉の存在できる領域の面積は、
4個のパチンコ玉の配置によって、複雑に変化する。
2個から3個、4個とパチンコ玉の数が増えていっても、 基本の考えは変わりません。 しかし、パチンコ玉の存在できる面積の計算は急速に難しくなっていきます。 たとえば4個のパチンコ玉が図2-3 のように配置している時、 5個目のパチンコ玉が存在できる面積を考えてみましょう。 図2-3の左端の場合には容易に計算できますが(L2 - (π/4))、 図2-3の真ん中の配置では2つの円同士の重なりの面積が入ってきてちょっと厄介です。 これがさらに一般的な場合、 例えば図2-3の右端になると、多数の円の重なりの評価が必要になり、 解析的な評価は絶望的になってきます。 液体の統計力学をめぐる困難は、ここにあるといってもよいのです。
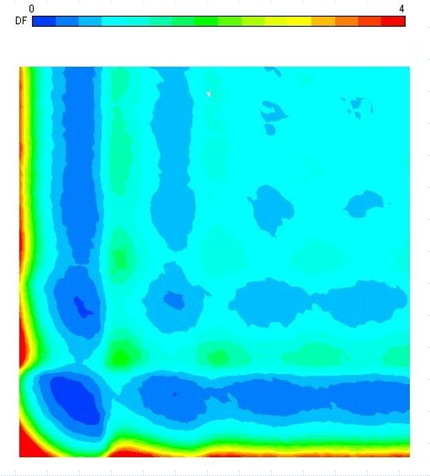
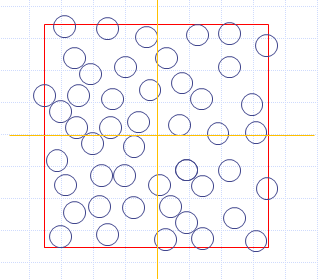
今日では、 多数の粒子が存在する場合の存在確率の計算、 つまりは存在可能領域の面積の計算のために、 コンピューターを用いた種々の手法が用いられるようになりました。 モンテカルロ法はその代表的な手法で、 図2-4には箱の中に49 個のパチンコ玉を入れて、 箱の中のパチンコ玉の分布を計算した例を示します。 この計算結果は、 ここまでのお話で言えば、 48 個のパチンコ玉を箱の中に詰めていろいろ動かしたとき、 49 番目のパチンコ玉が入れる隙間がどのあたりにできるか、 パチンコ玉の存在確率がどの程度かを計算したことに相当しています。 結果を見ていただくと、 パチンコ玉は図2-2 で見たように、 箱の隅の方、 1個のパチンコ玉を最初に置いた時に排除領域が小さいところに、 高い確率で存在します。 しかし多数のパチンコ玉が存在することで、 複雑な山あり谷ありの構造が形成されます。
図2-4 の結果はいろいろ示唆に富んでいます。 ここで取り上げるパチンコ玉からできた流体のように、 引力的な相互作用のない系では、 分子は均一に分布するような描像が暗黙の内に仮定され、 静電的な相互作用や水素結合、 π電子間の相互作用などといったもので、流体中の分子の分布が議論されることがあります。 そうした議論はまったくの誤りというわけではありませんが、 大事なポイントを外しています。 分子間の斥力的な相互作用の組み合わせ、 いわば分子のパッキングの効果で、 種々の複雑な分子分布が実現され得るのです。 それはまた日常の経験の中でも、満員電車の中で、 扉に接したところ、 凹んだ角になったところの居心地がよい、 という形で経験するところでもあるでしょう。
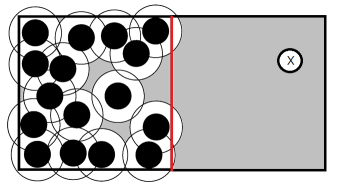
ここまでは粒子の存在確率という観点で眺めてきましたが、これを熱力学量に引き付けて考えてみることもできます。 図2-5 のようにある特定のパチンコ玉 X のみを透過することのできる、半透膜を考えてみましょう。 半透膜をはさんで、一方は他のパチンコ玉が存在しない状態、 もう一方には多数のパチンコ玉が存在していて、 両方の箱の大きさは同じだとします。
Δμ° = -T ln <Vf>/V
こうした話を聞くと、皆さんはたかが面積(体積)の計算じゃないかと思われるかもしれません。 実際そうなのです。 液体の平衡状態の統計力学の核心部分は、面積(体積)の計算にあるといってよいのです。 パチンコ玉が2個の場合は高校程度の知識でも何とかなります(逆三角関数が出てきますが)。 しかし図2-3 でも見たように、パチンコ玉の数が増えるにしたがって面積の計算は急速に難しくなって行き、 図2-4 に見るような複雑な流体構造、 あるいは種々の流体の熱力学的な個性を生み出すのです。 面積計算がパチンコ玉のような単純な形状の分子についてさえきわめて困難であること、 これが液体の統計力学の一筋縄でいかない部分であり、 「たかが面積、されど面積と」言いたいところです。
*2
「粒子がどこにあるか」「壁がどこにあるか」というのは、
まじめに考えると意外に厄介な問題です。
ここではパチンコ玉の中心(相互作用の中心)を、パチンコ玉の存在する場所とし、
パチンコ玉の中心が閉じ込められている領域の境界を器壁と考えます。
パチンコ玉が、境界線からパチンコ玉の半径入ったところで跳ね返されるといった描像をとることも可能ですが、
そのように器壁の位置を指定すると、異なるサイズのパチンコ玉については存在できる領域の大きさが変化し、取り扱いが厄介になります。