ありふれた液体は古典統計力学に従うものとみなせます。 この「古典統計力学に従う」というのは、 平衡状態で分子の速度(運動量)と位置が統計的に独立な量として扱えるということです。 まずこのことの重要性をよく認識していただく必要があるかと思います。
f(v) = C exp(-mv2/2T)
しばしば見過ごされているようですが、 このマクスウェルの速度分布則の大きなポイントは、これが密度や圧力に依存しないことです。 つまり気体でも液体でも、温度が同じなら分子の速度分布は変わらないのです。 液体中では「分子運動が遅い」、 「運動エネルギーが小さい」ように語られることがありますが、注意が必要です。
また気体の凝縮、液体の蒸発に関わって、 「運動エネルギーを失って凝縮する」 「運動エネルギーを得て蒸発する」といった表現が用いられます。 一見もっともらしく聞こえますが、正しくありません。 エネルギーの大きさを考えて見ても、 水の蒸発には44 kJ/mol(25 ℃。100 ℃では41 kJ/mol)のエネルギーが必要ですが、 運動エネルギーはせいぜい4~5 kJ/molで、1ケタ違います。
直感的には、蒸発では周りの分子からの束縛を振り切って自由になるわけですから、 それには運動エネルギーが必要であり、
「温度を上げると運動エネルギーを得て蒸発する」
のは極めて自然な主張であるように見えます。 けれども圧力を低くしても水は蒸発します。
「圧力を下げると運動エネルギーを得て蒸発する」
のでしょうか? このあたりの事情を考えてみていただけると、話が単純でないことをご理解いただけるでしょう。
同様に
「気体が溶解する時、運動エネルギーを失うので発熱する」
といった説明がなされることがあります。 これも正しくありません。 これは温度を上げた時に気体の溶解度が下がることの定性的な説明には都合がよいのですが、 気体の溶解度は温度を上げると大きくなることもあるのです。 ごく身近な例でいえば、60 °C以上では窒素の水への溶解度は温度とともに大きくなります。*2 「液体に溶解すると運動エネルギーを失う」といった考えに縛られていては、 こうした何でもない現象を見落とす危険すらあります。
このような話が出てくると、 「量子力学的な効果があるから気体中の方が運動が激しい」 といったことを考える人がいるかもしれません。 量子論的な効果がどれほど現れるかを評価する方法として、 平面波基底を用い状態和(分配関数)Z を、プランク定数 hの巾で展開する手法があります。 それによると状態和に対する量子論的な補正は次式で表わされます (添え字の cl 古典的に扱った場合を意味します。ここでは記号等の詳細は無視して眺めてください):
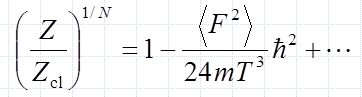
分子に働く力 F が大きいほど、 分子の質量 m が小さいほど、温度 T が低いほど、 量子論的な補正は大きくなるわけですが、 ふつうの液体について評価して見ると、 この補正は万分の1程度の数字になってきます。 しかもこの補正を施すと、運動エネルギーは大きくなります(調和振動におけるゼロ点エネルギーを思い出していただければよいでしょう)。 つまりふつうの液体については、量子論的な補正は小さく、 しかもそれを考慮すれば液体中の方が、 気体中より激しく運動しているわけです。
*2
気体の体積一定の条件の下での溶解度(オストワルドの溶解度)を考えます。
分圧一定の条件ではPV仕事に相当するエネルギーが必要で、
溶解度の極小はより高温側に現れます。