|
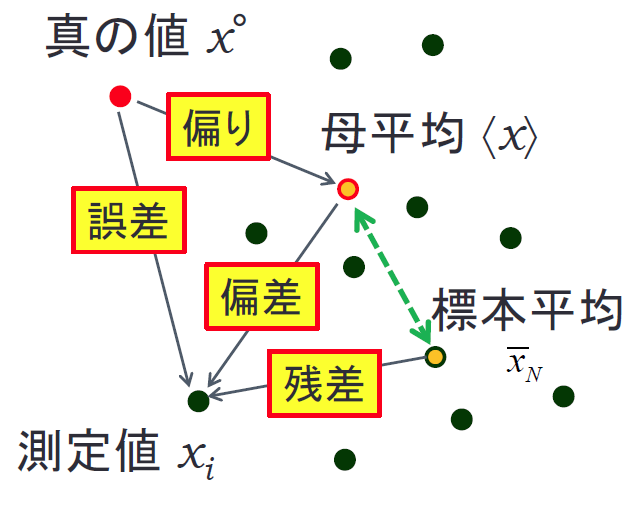
| 図 1-1.誤差をめぐる諸量 |
「真の値」\(x^{\circ}\) をえるために、 何回か測定をして \(x_i ~ (i = 1, 2, \ldots) \) という値を得たものとしましょう。 測定値の誤差 \(\Delta x_i\) というのは、真の値からの外れで表されます。
\begin{equation} \Delta x_i = x_i - x^{\circ} \label{eq:DefErr} \end{equation}
測定にばらつきは付きものですが、何回も何回も測定して平均をとれば、ばらつきの影響は除けます。 平均することでばらつきの影響を除いた値を母平均と呼び、 ここでは \(\langle ~~ \rangle \) でくくって表します。 この母平均 \(\langle x \rangle\) が、測定で得られるまっとうな値であると考えられます。 けれどもこれが真の値と一致するとは限りません。 たとえば滴定値でいうと、使っているビュレットの目盛付けが間違っていたら、読み取った値は真の値から外れています。 こうした測定値と真の値との差を偏り(バイアス bias)と呼び、ここでは添え字を付けない \(\langle \Delta x \rangle\) で表すことにします:
\begin{equation} \langle \Delta x \rangle = \langle x \rangle - x^{\circ} \label{eq:DefBias} \end{equation}
また誤差からこの偏りを差し引いたものを偏差(deviation)と呼び、 ここでは \(\delta x_i\) で表すことにします (偏差の生じることを、ばらつき(dispersion)と呼びます):
\begin{equation} \delta x_i = \Delta x_i - \langle \Delta x \rangle = x_i - \langle x \rangle \label{eq:DefDev} \end{equation}
偏差の母平均は 0 になり、 偏差、ばらつきの大きさを表すのに、 その2乗の平均である分散 \(\sigma_x^2\)、 あるいは分散の平方根の標準偏差 \(\sigma_x\) が採用されます。
\begin{equation} \langle \delta x_i \rangle= 0\\ \sigma_x^2 = \langle (\delta x_i)^2 \rangle \label{eq:variance} \end{equation}

|
| 図 1-1.誤差をめぐる諸量 |
さて何回も測定して得られるであろう母平均に注目しましたが、 実際には限られた数 \(N\) 回の測定の結果得られる標本平均 \(\bar{x}_N\) を得ることができるだけです。
\begin{equation} \bar{x}_N = \frac{1}{N} \sum_{i = 1}^N {x_i} \label{eq:smean} \end{equation}
十分多数回測定すれば、標本平均は母平均に漸近しますが(大数の法則)、 有限回の測定で考える時には、式 \eqref{eq:DefDev} の偏差の代わりに残差 \(x_i - \bar{x}_N\) を用いた議論が登場します (標本標準偏差を求めるのに残差二乗和を作るのはおなじみでしょう。 もっともここでのお話では、このあたりの話題は端折らせていただきます)。 標本平均のばらつきはまた後で考えるとして、 ここまでに出てきた概念の見取り図を、図 1 に示します。 なお、系統誤差、偶然誤差という言葉が使われることがありますが、 これはそれぞれ、偏り、偏差(ばらつき)に相当します。
実際にはいくつかの測定値にさまざまな演算を施して、 最終的な結果を得ます。 ここでは四則演算にともなう誤差を考えます。 なお測定値 \(x\) の大きさに比べて、誤差 \(\Delta x\) は十分小さいものとします (たとえば滴定値 12.20 mL に対し、0.02 mL の誤差といった程度)。
\begin{equation} |x| \gg |\Delta x| \label{eq:errScale} \end{equation}
ある測定値 \(x\) に線形の変換(定数 \(a\) をかけて定数 \(b\) を足す)を行った時、 誤差は \(x\) の \(a\) 倍になります。 また2つの測定値 \(x\) と \(y\) を加減したものの誤差は、 \(x\) と \(y\) の誤差の加減になります。
\begin{eqnarray} \Delta (ax + b) &=& (a x + b) - (a x^\circ + b) = a \Delta x \label{eq:errRel1a} \\ \Delta (x \pm y) &=& (x \pm y) - (x^\circ \pm y^\circ) = \Delta x \pm \Delta y \label{eq:errRel1b} \end{eqnarray}
誤差の偏り(バイアス)は、 式 \eqref{eq:errRel1a}、\eqref{eq:errRel1b} の平均を取ればよいわけですから、 \(\langle \Delta (ax + b) \rangle = a \langle \Delta x \rangle\) などとなるだけで簡単です。 けれども偏差、ばらつきの大きさについては分散を評価する必要があり、 単純ではありません。
\(x\) に式 \eqref{eq:errRel1a} のような線形の変換を行った時、 分散は、元の \(x\) の分散の \(a^2\) 倍になります。
\begin{equation} \langle (\delta (ax + b))^2 \rangle = \langle (\delta (ax))^2 \rangle = a^2 \langle (\delta x)^2 \rangle \label{eq:errRel2} \\ \sigma_{ax + b} = |a| \sigma_{x} \end{equation}
2つの測定値 \(x\) と \(y\) を加減したものの偏差の分散を評価するには、 \(x\) と \(y\) のばらつきの共分散、 \(\langle \delta x \delta y \rangle\) を考える必要があります。 \(x\) と \(y\) の測定が、別個に行われている、 独立の測定であるとすると、 \(\langle \delta x \delta y \rangle = \langle \delta x \rangle \langle \delta y \rangle = 0\) より、次式が成り立ちます。
\begin{eqnarray} \langle (\delta (x \pm y))^2 \rangle &=& \langle (\delta x)^2 \rangle \pm 2 \langle \delta x \delta y \rangle + \langle (\delta y)^2 \rangle \\ &=& \langle (\delta x)^2 \rangle + \langle (\delta y)^2 \rangle \label{eq:errRel3} \end{eqnarray}
これらの関係を用い 式 \eqref{eq:smean} の標本平均の偏りと分散を求めると次のようになります:
\begin{equation} \langle \Delta \bar{x}_N \rangle = \langle \bar{x}_N - x^\circ \rangle = \frac{1}{N} \sum_{i = 1}^N {\langle x_i - x^\circ \rangle } = \langle \Delta x \rangle \label{eq:smean_bias} \end{equation}
\begin{equation} \langle (\delta \bar{x}_N)^2 \rangle = \frac{1}{N^2} \sum_{i = 1}^N {\langle \delta (x_i)^2 \rangle } = \frac{\langle (\delta x)^2 \rangle }{N} \label{eq:smean_var} \\ \sigma_{\bar{x}_N} = \frac{\sigma_x}{\sqrt{N}} \end{equation}
ここで \(N\) 回の測定はそれぞれ独立で(\(\langle \delta x_i \delta x_j \rangle = 0,~~ i \ne j\))、 偏り \(\langle \Delta x \rangle \) 、分散 \(\langle (\delta x)^2 \rangle \) が等しいとしています。
測定を \(N\) 回行うと、 偏りを取り除くことはできませんが、 偏差、ばらつきは \(1/\sqrt{N}\) に比例して小さくなります。 最初に述べた「何回も何回も測定して平均をとれば、ばらつきの影響は除けます」 というのはこのことに対応します。
もっぱら測定値の加減算の誤差をみたのですが、 最後に乗除の誤差についても見ておきましょう。 乗除で得られる値の相対誤差は、下式のように \(x\) と \(y\) の相対誤差\(\Delta x/x^\circ\)、\(\Delta y/y^\circ\) の加減で与えられます。 たとえば縦 3.00 m、横 2.50 m の長方形について、 実際に測った時、縦 3.03 m、横 2.45 m だったとすると、 面積の相対誤差は 0.03/3.00 + (-0.05)/2.5 = -0.01 というわけです。
\begin{equation} \frac {\Delta (x y)}{x^\circ y^\circ} \approx \frac {\Delta x}{x^\circ} + \frac {\Delta y}{y^\circ} \label{eq:errRel4} \\ \frac {\Delta (x/y)}{x^\circ /y^\circ} \approx \frac {\Delta x}{x^\circ} - \frac {\Delta y}{y^\circ} \end{equation}
式 \eqref{eq:errRel4} の関係は、次の計算で \(\Delta x \Delta y \sim 0\)、\(1 + \Delta y/y^\circ \sim 1\) に注意すれば導かれます。 あるいは \(x\)、\(y\) を正であるとし、 \(\ln (x^\circ + \Delta x) \approx \ln x^\circ + \Delta x/x^\circ\) といった関係に注目してもよいでしょう。 \[ \Delta (x y) = (x^\circ + \Delta x) (y^\circ + \Delta y) - (x^\circ y^\circ) \approx y^\circ \Delta x + x^\circ \Delta y\\ \Delta (x/y) = \frac{x^\circ + \Delta x}{y^\circ + \Delta y} - \frac{x^\circ}{y^\circ} = \frac{x^\circ}{y^\circ} \left [ \frac{\Delta x/x^\circ - \Delta y/y^\circ}{1 + \Delta y/y^\circ} \right ] \approx \frac{x^\circ}{y^\circ} (\Delta x/x^\circ - \Delta y/y^\circ) \]
また \(x\) と \(y\) の乗除の偏差の分散については、 式 \eqref{eq:errRel4} から、次の関係が成立します。 乗除の結果の分散の相対値は、 元の \(x\) と \(y\) の相対分散の和で与えられます。
\begin{eqnarray} \frac{\langle (\delta (x y))^2 \rangle}{(x^\circ y^\circ)^2} & \approx & \frac{\langle (\delta x)^2 \rangle}{{x^\circ}^2} + \frac{\langle (\delta y)^2 \rangle}{{y^\circ}^2} \\ \frac{\langle (\delta (x/y))^2 \rangle}{(x^\circ /y^\circ)^2} & \approx & \frac{\langle (\delta x)^2 \rangle}{{x^\circ}^2} + \frac{\langle (\delta y)^2 \rangle}{{y^\circ}^2} \label{eq:errRel5} \end{eqnarray}
測定に関わる偏り(バイアス)、偏差(ばらつき)などについて見たわけですが、 かりに偏り\(\langle \Delta x \rangle\)がわかっておれば、 \(N\) 回の測定の結果得られる標本平均 \(\bar{x}_N\) から、 次の量 \(x^{*}\) を求めれば、
\begin{equation} x^{*} = \bar{x}_N - \langle \Delta x \rangle = \bar{x}_N - (\langle x \rangle - x^\circ) \label{eq:calbA} \end{equation}
\(\langle x^{*} - x^\circ \rangle = 0\) ですから、 「真の値」\(x^\circ\) が、偏差(ばらつき)の分散
\begin{equation} \langle (\delta x^{*})^2 \rangle = \frac{\langle (\delta x)^2 \rangle}{N} \label{eq:calbB} \end{equation}
で求められたことになるわけです。 こうやって得られた値の不確かさを考える時、 真の値にどれくらい近いか、 そしてばらつきがどれくらい大きいか、 というのを議論することになります。
このあたりを語る「ことば」に、今もいささか混乱があるので、 少し整理しておきます。 真の値にどれくらい近いかを、 「正確さ」(あるいは「真度」)と呼び、 ばらつきがどれくらい小さいかを、 「精密さ」(あるいは「精度」)と呼びます。 無論「正確さ」と「精密さ」を兼ね揃えたのがいいわけですが、 こうした観点からの不確かさについての評価を「精確さ」と呼びます。 (JIS Z8103:2019 「計測用語」)
以前、計測用語の世界では「精確さ」を「精度」と呼んでいましたが、
2019年に JIS Z8103 が「精密さ」を「精度」と呼ぶように改訂され(以前は「精密度」)、
他の規格との整合が図られました。
なお「正確さ trueness」という概念はなじみが薄いかもしれません。
ぼくが学生時代は、誤差の話は precision と accuracy の2本立てで行われていました。
どうやらその後、”真なるもの” をめぐる議論に関わって、
trueness という概念を導入して議論の整理がおこなわれたようです。

|
| 図 2. 標準温度計の検査成績書。 これはメーカーで検査したものだが、 さらに上位の計量標準総合センターでの検定を受けたりすると、 「基準温度計」などと呼ばれ、値段も跳ね上がる (温度計の構造も、外気の影響を受けにくい2重管型になる)。 |
実際の測定において、較正 calibration(あるいは補正 correction)というのは、偏り(バイアス)を減らす操作に相当します。 たとえば標準温度計として市販されているガラス温度計には、 検査成績表が付いてきて、「器差表」というのが書いてあったりします。
器差というのは、この温度計を使って読み取るであろう温度 \(\langle x \rangle\) から真の温度 \(x^\circ \) を引いたもの \(\langle x \rangle - x^\circ \) 、 ここでいう偏り(バイアス) \(\langle \Delta x \rangle\) になっています。 ですからたとえば器差表に 25 °C での器差が +0.03 °C となっておれば、 標準温度計の示度が 25.55 °C の時、真の温度として 25.52 °C を取れば、 その時々の温度の不均一性などの影響によるばらつきを除けば、精確な温度を与えるわけです。 なお余談ですが、 メーカーによっては「補正表」が付いてくることがあります。 補正表に示されている補正値というのは、真の温度から示度を引いたもの \(x^\circ - \langle x \rangle\) になっていて、 較正に当たっては引くのではなく、足すことになります。 器差と混同すると、較正しない方がよかったという残念な事態になるのでご用心 (図 2 の温度計の検査成績書には、こうした問題を避けるためか、 器差や補正値ではなく、単に正確な温度における示度が書かれています)。
温度計の較正操作に見るように、 あらかじめ偏りが知られている場合はそれでいいのですが、 日によって装置の調子が違い、偏りが変動する場合も少なくありません (温度計の較正値もメーカーの保証期限がくると、厳密には較正のやり直しが必要)。 そういう場合には、 何かある精確な値、 参照とできる値 \(y^\circ\) を与えるものがあるならば、 その測定値 \(\bar{y}_N\) を得て、測定の偏り(バイアス) \(\langle \Delta x \rangle\) を知ることができます (標準温度計についてくる「器差」や「補正値」も、こうした参照値からの偏りを示すものと見ることができます)。
\begin{equation} \langle \Delta x \rangle = \langle \Delta y \rangle = \langle \bar{y}_N \rangle - y^\circ \label{eq:refstate} \end{equation}
最近のちょっと上等な化学天秤では、 較正の必要性を自動で判断して較正操作が行われるようになっていて、 「何か天秤がうなっている」程度で、ことさらに意識されることはないかもしれませんが、 こうした操作は当たり前に行われています。 またpH 測定などでも、よく出会うところです。
参照できる値 \(y^\circ\) が利用できない場合、 あるいは偏りの評価に手間がかかる場合も少なくありません。 そうした場合には偏り(バイアス)を打ち消すように実験を構成することが考えられます。 ここではビュレットの読み取り誤差について考えましょう。
|
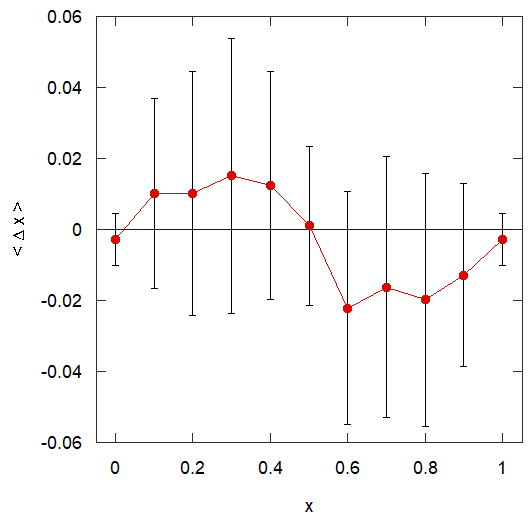
| 図 1. 読み取り誤差の実験の結果 (65人、2473件の結果から作成)。 設定された値 \(x^\circ\) を、 マウスでクリックした位置の値 \(x\) から引いた \(\Delta x \) の平均 を \(x^\circ\) に対しプロットしてある。 バーは標準偏差 ±σに対応。 |
学生実験の容量分析の実験では、 ビュレットの目盛りを最小目盛の 1/10、0.01 mL まで読むわけですが、 0.1 mL おきの目盛り線の中間地点 0.05 mL を読み取るより、 中途半端な 0.03 mL を読み取る方が難しそうです。 こうした目盛りの読み取り誤差について、 当化学教室の新3回生諸君に web 上で行う簡易なシミュレーション実験で取り組んでもらった結果を図 1 に示しました。 シミュレーションでは目盛りの 0.1 刻みの位置に 0.01 程度の精確さでマウスカーソルを合わせてもらいます。 実験結果では、どの目盛り位置でも、だいたい ±0.05 には収まっていますが、 総括的に見ると2割ぐらい ±0.05 以上の誤差が生じています。 また 0.0 ~ 0.5 と 0.5 ~ 1.0 では、 読み取りの誤差は正負、逆方向に出る傾向(偏り)があります。 さらにここでは示していませんが、 個人差が大きいです(どうも老人は苦手のようです・・・)。
この読み取りの誤差の偏りを、 実際の滴定値にどのように較正すればよいでしょうか? 図1の web 上のシミュレーションの結果を、 そのまま信じて処理するのもアリかもしれません。 けれども実際のビュレットの目盛りはもっと細かく、 液面のメニスカスは曲がっていて、 ディスプレイ上のマウスクリックのようには行きません。 また個人差が大きいので、他人の結果をそのまま利用するわけにはいきません。 それでは、こうしたシミュレーションではなく、 実際にビュレットを使って、各自で読み取り誤差を調べる必要があるでしょうか? こうした時に使えるのが、 (当たり前のように行っていますが)滴定前後での読み取りの値の差を取るという方法です。
これは2つの読み取り値 \(x\)、 \(y\) についてその差をとると、 それぞれの値の偏り \(\Delta \langle x \rangle\) と \(\Delta \langle y \rangle\) が打ち消すだろうという考えです:
\begin{equation} y - x = (y^\circ - x^\circ) + (\Delta \langle y \rangle - \Delta \langle x \rangle) + (\delta y - \delta x)\\ \langle y - x \rangle = \langle y^\circ - x^\circ \rangle \label{eq:setout} \end{equation}
差を取ることによって得られる滴定値 \(y - x\) についての偏りは除かれます (\(\langle y^\circ - x^\circ \rangle\) と真の値について平均化操作を施しているのは、 目盛位置が実験のたびに変動することを見込んでいるからです)。 ただしその標準偏差は \(\sqrt{2}\)倍になります。 けれどもこの程度のばらつきについては、測定回数を増やすことで対処可能な誤差なので、 偏りを除くことを優先するのです。
\begin{equation} \langle (\delta(y - x))^2 \rangle = \langle (\delta x)^2 \rangle + \langle (\delta y)^2 \rangle \approx 2 \langle (\delta x)^2 \rangle \label{eq:setout_var} \end{equation}
ここで注意が必要なのは、 \(x\) と \(y\) がそれぞれ同じように測定されている(偏りが同じ)ということです。 仮に液面の位置をちょうど目盛の切りのいいところ(たとえば 1.00 mL)に調整してから滴定を行うのは (こういう手法を推奨する向きもあります)、 ばらつきは小さくなりますが、 偏りが打ち消されず、原則として好ましくありません。
せいぜい数回の滴定について、 それも 1/1000 になるかどうかという問題について (学生実験では 10 mL 程度の滴定量について、0.01 mL まで読み取る)、 こうしたことをあげつらうのは無駄だという考え方はありえます。 しかし少なくとも「教育的」には、 大事なポイントであると思っています (実験計画法をご存じの方は、 フィッシャーの3原則(繰り返し、ランダム化、局所管理)に照らしていうと、 ここでの操作がランダム化に相当しているにお気づきでしょう)。
長々と誤差にまつわる話をしてきたわけですが、 最後に測定に当たっての心得として、 「偏りのない独立な」測定を行うことの重要性を強調しておきたいと思います。
先に見たように、実験を繰り返すことで偏差 \( \delta \bar{x}_N \) は小さくすることができますが、 偏り(バイアス) \( \langle \Delta x \rangle \) を除くことはできません。 このあたりの事情を見るのに、 ぼくがよく出すのは、有効数字の計算です。 次の計算を考えてみてください。
両方とも有効数字の計算のルールに則っていることはお分かりでしょう。 でも出てくる結果は、有効数字 3 ケタと 4 ケタで違っています。
このことの背景にあるのは、 a では同じ数値の 10 倍であるのに対し、 b ではそれぞれ異なる測定によって得られた数値を問題にしていることです。 かりに問題にしている数値が 3.670 ± 0.005 (標準偏差が 0.005)とします。 a の場合には先の式 \eqref{eq:errRel2} から標準偏差は 10 倍(分散は 102 = 100 倍)、 36.70 ± 0.05 なので36.7 にして、 b の場合には式 \eqref{eq:errRel3} から標準偏差は \(\sqrt{10} \approx\) 0.31 倍(分散は 10 倍)、 36.70 ± 0.016 なのでこれを有効数字 3 ケタに丸めるには忍びないので 36.70 にしたわけです (このあたりは有効数字の取り扱いの妥協的な部分)。 足し算の場合にこうした扱いになるのは、式 \eqref{eq:smean_var} の標本平均の計算で見たように、 それぞれが独立な測定であるからです(\(\langle \delta x_i \delta x_j \rangle = 0,~~ i \ne j\))。 b の足し算記号「+」には、繰り返し実験しては「また 3.67 か」という、 人間のため息が隠されていると思えばよいかもしれません。
ところでこの有効数字の計算で、扱っているのが 3.670 ± 0.005 と考えて議論しました。 でもこれが 3.673 ± 0.005 だったらどうでしょう? この時、これを 10 回足しこんだ計算の結果は 36.73 ± 0.016 になっているでしょう。 そしてこの場合には、10 回とも 3.67 というのではなく、たとえば3 回ぐらい 3.68 が登場して、 3.67 + 3.67 + 3.68 + 3.67 + 3.67 + 3.67 + 3.67 + 3.68 + 3.68 + 3.67 = 36.73 といった計算になったケースが多いであろうことが予想されます。 個々の測定値を見ていてもなかなか気づきませんが、 多数回の測定の結果から、こうしたちがいが浮かび上がってくるので注意が必要です。 くれぐれも、小さくとも偏りはできるだけ消すこと、 それぞれの測定はできるだけ独立に行うことを心がけるべきです。