これは B3 実験の準備実験の課題説明のプリントでした。 準備実験のレポートシートはこちら
当方で予定していた計算は次のとおり (\(a \ne 2m \pi\)。 \(\Im (z)\) は \(z\) の虚部を与える関数。 2行目のように対称化操作を施すと話が簡単になる。 無論 \(a = 2m \pi\) の時は \(f(x) = (N + 1) \sin x\)):
\begin{eqnarray} f(x) &=& \sum_{n=0}^N \sin (x + na) = \Im \left[\sum_{n=0}^N \rme^{\rmi(x + na)} \right] = \Im \left[ \rme^{\rmi x} \frac{1 - \rme^{\rmi (N+1) a}}{1 - \rme^{\rmi a}} \right] \nonumber \\ &=& \Im \left[ \rme^{\rmi x} \frac{\rme^{\rmi (N+1) a/2}}{\rme^{\rmi a/2}} \frac{\rme^{-\rmi (N+1) a/2} - \rme^{\rmi (N+1) a/2}}{\rme^{-\rmi a/2} - \rme^{\rmi a/2}} \right] = \Im \left[ \rme^{\rmi (x + N a/2)} \frac{\sin{(N+1) a/2}}{\sin{a/2}} \right] \nonumber \\ &=& \frac{\sin (N+1) a/2}{\sin (a/2)} \sin (x + N a/2) \label{eq:qq} \end{eqnarray}
皆さんの結果の多くもこの線を踏襲したものでしたが (力でねじ伏せたり、天才的なひらめきで一挙に導出した人もありました)、 三角関数の積和・和積の公式を利用した次のような解を示してくれた人もあったので紹介しておきます(少し簡単化してあります):
\begin{eqnarray} 2 \sin(a/2) f(x) &=& \sum_{n=0}^N 2 \sin(a/2) \sin(x + na) = \sum_{n=0}^N \left[ \cos(x + na - a/2) - \cos(x + na + a/2) \right] \nonumber \\ &=& \cos(x - a/2) - \cos(x + Na + a/2) = 2 \sin [(N+1) a/2] \sin(x + Na/2) \nonumber \end{eqnarray}
\begin{equation} f(x) = \frac{\sin (N+1) a/2}{\sin (a/2)} \sin (x + N a/2) \nonumber \end{equation}
かりに bk という wave を ah という wave をコピー(duplicate)して作ったとします。 この後、ah を変更しても bk が変更されることはありません。
実際コマンドウィンドウに次のように入力すれば (「variable fac = 2」は変数 fac を定義して 2 を代入するということ)
variable fac = 2↵ bk = fac*ah↵
bk は ah を 2 倍したものになりますが、 この後 fac = 1.9 としても bk は変わりません。 変えるにはもう一度 bk = fac*ah とする必要があります。こうした場合
bk := fac*ah
としておくと(「=」の代わりに「:=」を使う)、bk は fac と ah に連動して変化するようになり、 fac あるいは ah を変化させると連動して bk が変わるようになります。
先の級数の公式 \eqref{eq:qq} が成り立っているかどうかを確認するには、 次のようにすればよいでしょう (\(N\) = 5 のケースを考えます。 証明すべき式が実際に成り立つかどうか確認するのはよい習慣です。特にYYが出題している場合には・・・):
Variable a = Pi/6 //Piは円周率を与える関数(IgorではExcel同様Piは関数として扱う) Make/N=1024/D ah,bk // ahとbkという1024行のwaveを作成 SetScale/I x -18.85,18.85,"", ah,bk // ahとbkのスケールを -6π から6πで設定 ah := sin(x) + sin(x + a) + sin(x + 2*a) + sin(x + 3*a) + sin(x + 4*a) + sin(x + 5*a) bk := sin(3*a)/sin(a/2)*sin(x+5*a/2)
ここで ah と bk の定義式に「:=」が用いられていることに注意してください。 こうしておくと、ah と bk の wave の値には a の値が紐付けされた形になり、 a の変動がすぐに ah、bk に反映されるようになります。 こうしておいて ah と bk のグラフを書き、両者が a を変えても一致することを確認すればよいわけです。
さて ah の計算でずらずら式を並べるのが煩わしく感じる人も多いでしょう。 特に \(N\) を大きくして検証してみたいときには厄介です。 そうした向きは新しく関数を定義することが考えられます。 具体的にはマクロを作成したのと同様の手順で、 今度は「Macro」ではなく「Function」で始まる次のような記述をすればよいのです (気体の粘度の実験で新しい当てはめ関数を定義したと思いますが、その際にも Procedure window を開いてもらっていたら (ショートカット Ctrl+M)そこに関数が定義されているのが見えたはず):
Function mnk(N, x, a) // 関数の引数を定義。ここでの x, a はこの関数の内部でのみ有効な変数になる Variable N, x, a // 計算に必要な変数を定義 Variable i, y // yを初期化し、sin の値を足しこんでいく。 y = 0; // Function では for - endfor の構文が利用できる(Macro では不可) for(i=0; i <= N; i +=1) y += sin(x + i*a) endfor // 足しこんだ y の値を関数の値として返す return y End
こうした関数を準備し Variable N = 5, a = π/6 であれば
ah := mnk(N, x, a)

|
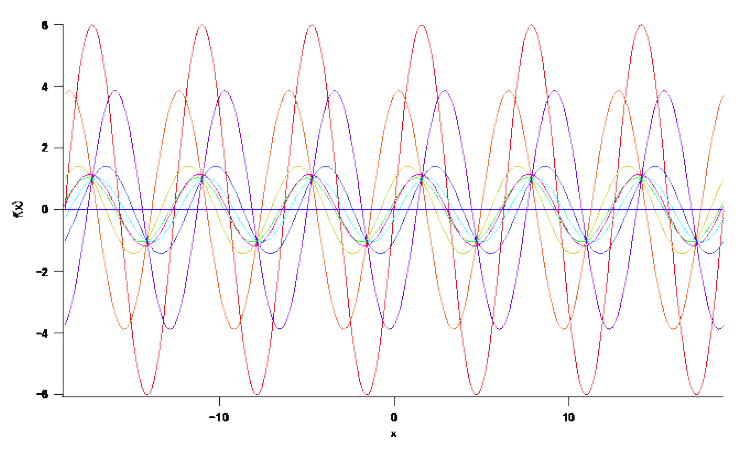
| 図 1. 種々の \(a\) に対する \(f(x)\) |
とすれば N = 5、a = π/6 の場合の wave を得ることができます。 こうして N や a の値を変えてた場合についても簡単に対応できます。 たとえば f(x) の図としては典型的には図1のようなものになるでしょう (a を π/6 刻みで変化させたもの)。
このように他の変数や wave に「紐付け」するのは便利ですが、 多用すると依存関係が複雑になって事態の収拾が困難になるので “見渡せる範囲”で使用するのがよいでしょう (例えば x := y, y:= z, z := x のような形で循環参照が生じる)。
なおこうした計算には Igor よりは他の数値計算専用ソフト SciLab(無料)、MatLab(有料) あるいはいわゆる数式処理ソフト Maxima(無料)、Mathematica(有料) などの方が向いているであろうことを付記しておきます。