確率と統計のはなし

あるランダム変数（確率変数）\(x\) が \(x\) の近傍 \(\rmd x\) の値をとる確率を \(f(x) \rmd x\) で表し、 \(f(x)\) を（確率）分布関数 (probability) ditribution function あるいは確率密度関数 probability density function と呼ぶ。分布関数 \(f(x)\) は 0 か正で、\(x\) を全領域について積分したものは 1 になる：

\begin{equation} f(x) \ge 0 ~~\mbox{かつ} ~~ \int_{-\infty}^{\infty} f(x) \rmd x = 1 \label{eq:rand1} \end{equation}

ここで分布関数 \(f(x)\) は密度であり、一般に単位があるということに注意する。ランダム変数が \(x\) 以下の値を取る確率

\begin{equation} F(x) = \int_{-\infty}^{x} f(x) \rmd x \label{eq:rand2} \end{equation}

を積算分布関数（累積分布関数とも） cumulative ditribution function と呼ぶ。 \(F(-\infty) = 0\)、\(F(\infty) = 1\) である。

ランダム変数（確率変数 stochastic variable）というのは、ある重み（確率）を背負った変数と考えられ、分布関数はその重みを表します。この分布関数という言葉は、結構便利づかいされるので、少し具体的な例に照らして、概念を整理しておきましょう。

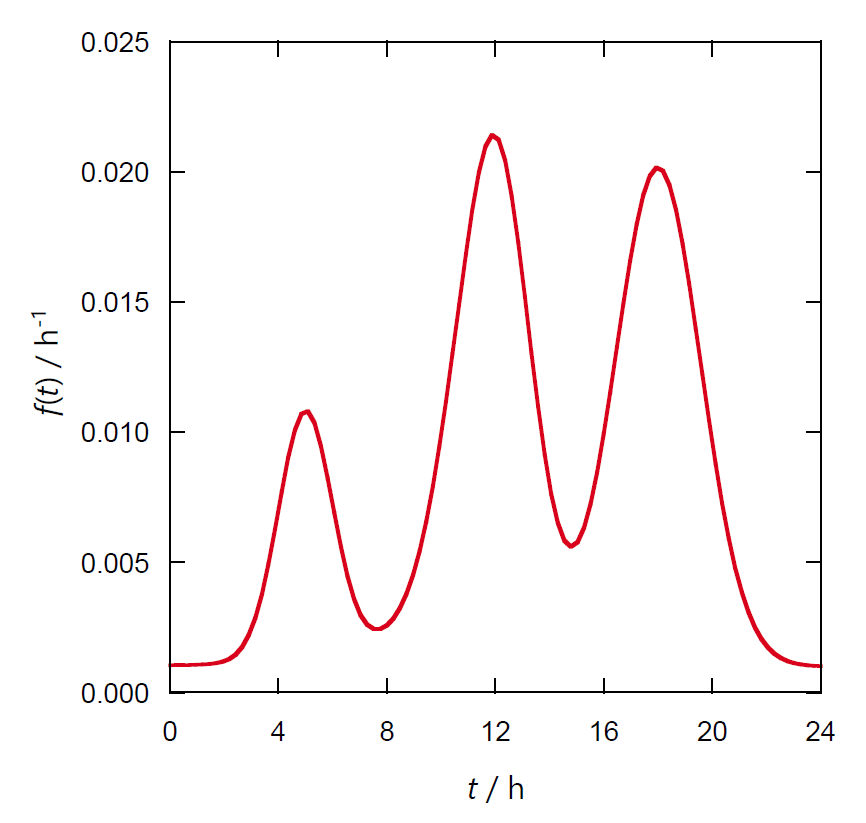
ある 24 時間営業の仮想的なコンビニ店で、1 日の来客数を調べて、来客の分布関数・積算分布関数を調べた結果、図 1-1 のようになったとしましょう。


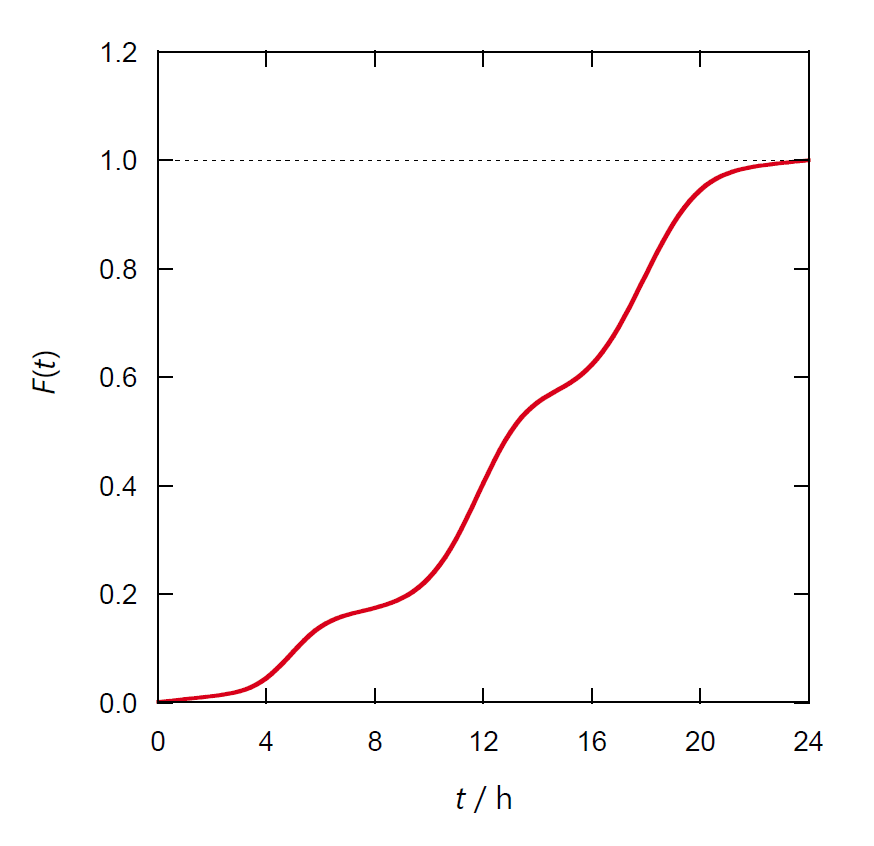
図 1a. 時刻ごとの来客の分布関数 \(f(t)\)。	図 1b. 1 日の来客の積算分布関数 \(F(t)\)。

ここでランダム変数として考えられているのは、来客時刻です。客の来る時刻はさまざまに変動し、それを捉えようとしたのが、図 1 に示す分布関数と積算分布関数になっています。分布関数からは 1 日の店の稼働状況、特徴が明瞭につかめます。朝が早い街らしく午前 5 時頃にピークがあり、12 時頃と退け時の午後 6 時頃にも来客のピークがあります。一方、店の売り上げに関心があれば、（客単価が変わらなければ）積算分布関数からは、早朝から店を開けなくても、 10 時開店で売り上げは 8 割弱程度は確保できそうだということが明瞭です。化学や物理の分野では、それぞれの現象の詳細な特徴に興味が向きがちで、積算分布関数よりは、その微分形である分布関数が前面に出てきます。

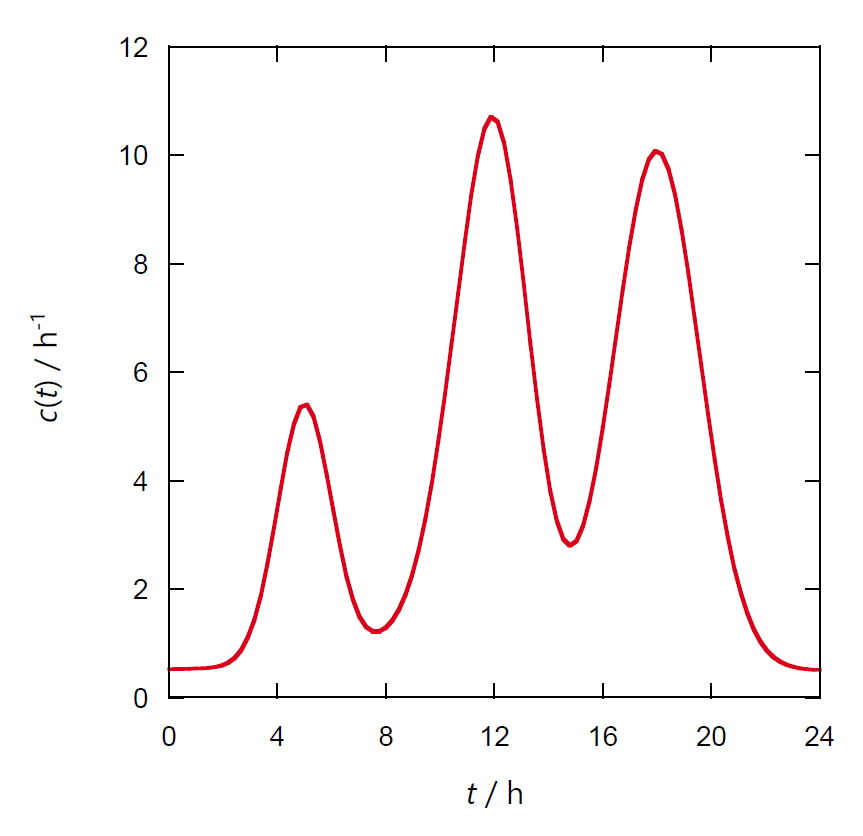
ところで実際上は、図 1 のような分布関数・積算分布関数よりは、次の図 2 のように来客頻度、来客数で見た方がしっくりくるでしょう。


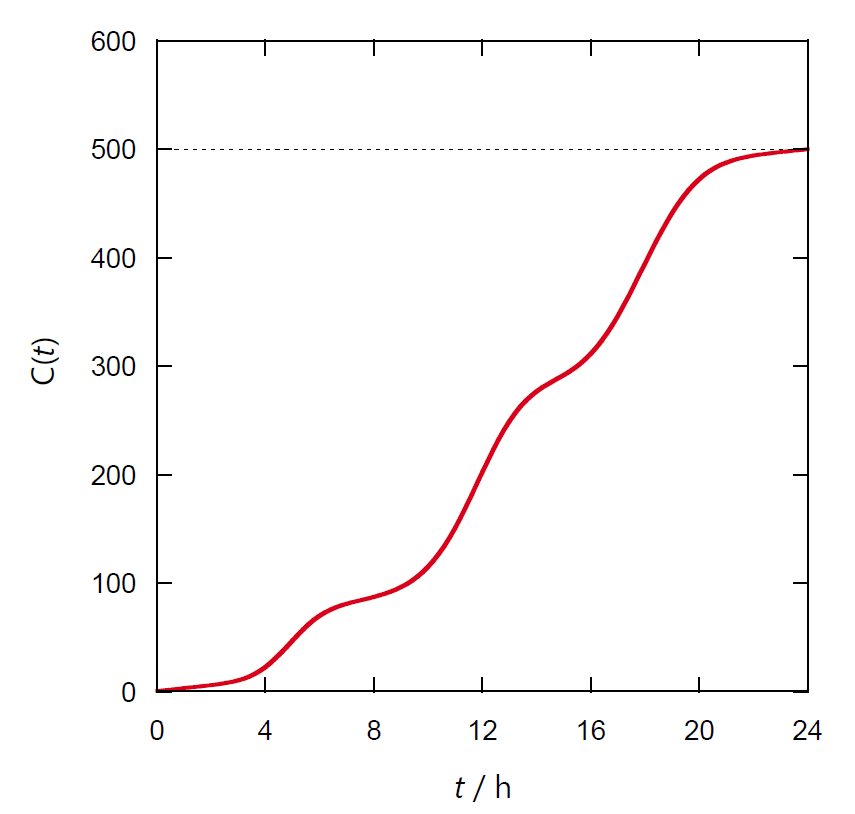
図 2a. 時刻ごとの来客頻度。	図 2b. 1 日の積算来客数。

図 1 と図 2 のグラフはただ縦軸の目盛りが変わっただけですが、図 2 のような表示の方が来客数と直接対応でき、時間帯ごとに必要な店員数や今後の経営計画（1 日の来客数 500 人ではちょっと苦しいか・・・）を考える上では便利です。実際、化学や物理の世界では図 2a の来客頻度のようなものを、「分布関数」と呼ぶことがしばしば（たいてい？）です。たとえば液体の構造に関わって登場する動径分布関数は、式 \eqref{eq:rand1} を満たさず、ここでいう分布関数ではありません。図 1 で縦軸はあくまで「確率」という、抽象化された「数」の世界のものですが、図 2 では「来客頻度」「来客数」という ”実体” をもったものです。このあたりは、数値と物理量の関係にも似ているかもしれません。

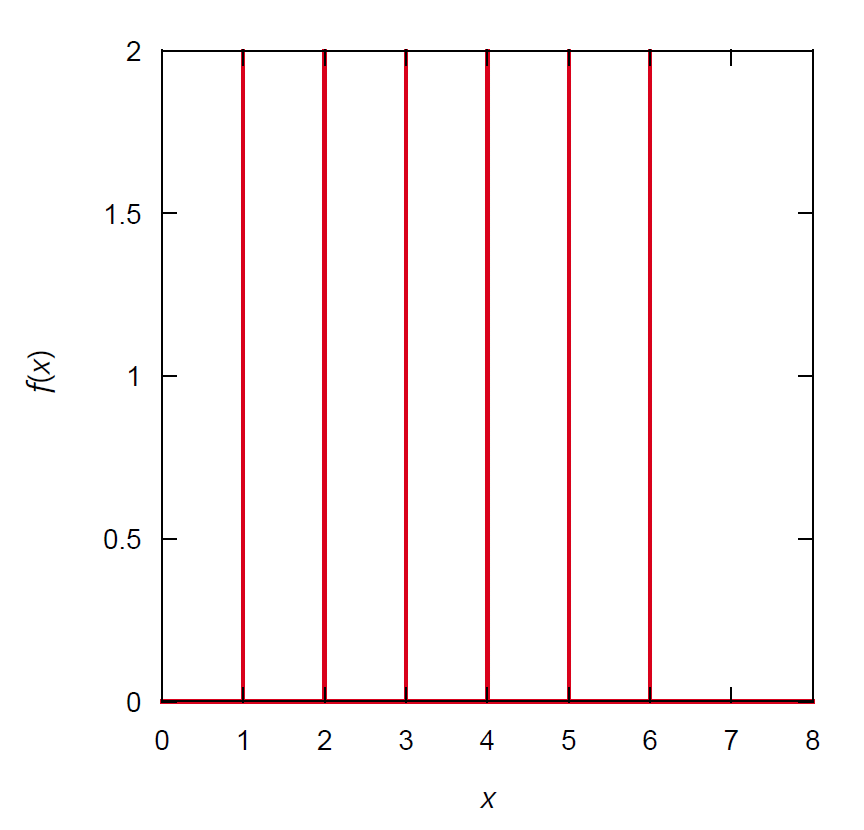
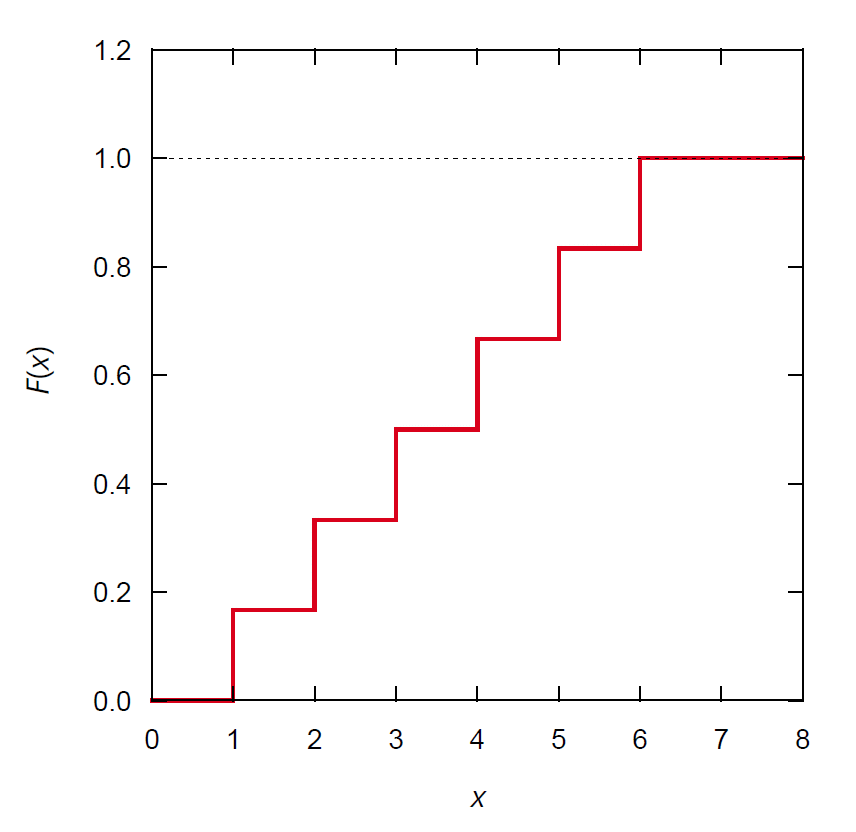
このおはなしでは、話を簡単にするためにランダム変数が離散的な場合は扱いません。離散的なランダム変数を扱う場合には、量子力学でお馴染みのデルタ関数が登場し、たとえばサイコロを振って出る目の場合、分布関数は \[ f(x) = (1/6) \sum_{i=1}^6 \delta (x - i) \] 積算分布関数は \[ F(x) = (1/6) \sum_{i=1}^6 U(x - i) \] となります（\(U(x)\) は単位関数）。


図 3a. サイコロの目の出る分布関数。	図 3b. サイコロの目の出る積算確率分布。

こういう場合、図 3a に見るように分布関数は多数のスパイクになって、もはや「絵」になりません。むしろ図 3b の方が状況の把握には適しているでしょう。また実際に事象を観測する際、多くの場合、ある閾（しきい）値を課して分布を知ることになります。

こういった事情もあって、分野によっては（特に数学では）積算分布関数を単に分布関数と呼び、分布関数を確率密度と呼びます。分野により、文脈により、「分布関数」という言葉で、単に事象の頻度を表す場合、また確率密度を指す場合や積算分布を指す場合があるので、注意する必要があります。

多変数の場合についても分布関数、積算分布関数が同様に定義され、 2 変数 \(x\)、\(y\) に対する分布関数 \(f_{x,y} (x, y)\) は次の性質を満たす：

\begin{equation} f(x, y) \ge 0 ~~\mbox{かつ} ~~ \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) \rmd x \rmd y = 1 \label{eq:rand3} \end{equation}

2 変数の積算分布関数 \(F_{x,y}(x, y)\) は、式 \eqref{eq:rand2} と同様に定義される。また一方の変数について全区間積分したものは１変数の分布関数になる：

\begin{equation} \int_{-\infty}^{\infty} f_{x,y} (x, y) \rmd y = f_x (x) ~~\mbox{あるいは} ~~ F_{x,y}(x, \infty) = F_x (x) \label{eq:rand4} \end{equation}

多変数の分布関数が１変数の分布関数の積で表されるとき、それぞれのランダム変数は統計的に独立であると呼ぶ。たとえば２変数 \(x\)、\(y\) が統計的に独立なら、次の関係が成立する：

\begin{equation} f_{x,y} (x, y) = f_x (x) f_y (y) ~~\mbox{あるいは} ~~ F_{x,y}(x, y) = F_x (x) F_y (y) \label{eq:rand5} \end{equation}

多変数の分布関数について、それぞれのランダム変数が統計的に独立でかつ同じ分布関数に従う場合は、特に重要でしばしば iid（IID、i.i.d. とされることもあります。independent and identically distributed）と略されます。

\[ f_{x_1,\ldots,x_n} (x_1,\ldots,x_n) = \prod_{i=1}^n f(x_i) \]

繰り返し実験で得られるデータは、この iid に従うことが期待され、実験データの取り扱いの基礎となります。

また理論的な取り扱いでもしばしば登場し、たとえばマクスウェルは速度分布則を導出する際に、等方的な分布を要請することで

\[ f_{x,y} (x,y) = \phi(x^2 + y^2) = f(x^2) f(y^2) \]

という関係式から（ここでは 2 次元にしておきます）、

\[ f(x^2) = \frac{1}{\alpha \sqrt{\pi}} \exp(- x^2/\alpha^2) \]

という分布関数を導いています（定数 \(\alpha\) は理想気体の状態方程式との対応から、温度、分子質量と関係づけられます。なお歴史的には、こうした取り扱いはガウスの誤差論の中で最初に登場したようです）。

１．ランダム変数と確率分布