3.アントラセンの二量化反応
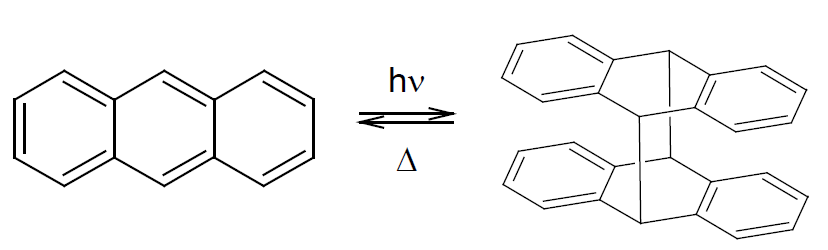
図8. アントラセンの光二量化
アントラセンの光二量化反応は古くからよく知られた光化学反応である。 ここではアントラセンの光二量化反応の生成物、およびその熱分解生成物を合成し、 それぞれの吸収スペクトルを測定し、アントラセンの光二量化反応について検討する。
- サンプル管にアントラセン0.05 g程度を取り、トルエン5 mLを加えて溶かす (ヒートガンで加温あるいは超音波洗浄機を用いてもよい)。
- ジェルネイル用紫外線照射装置に入れる。
- 30分~1時間程度紫外線照射を行うとジアントラセンの結晶が得られるので分取する。
- ジアントラセンをサンプル管に入れ、少量のトルエンにヒートガンで加熱しながら溶かした後冷却、 再結晶して精製する(量が少ないときは再結晶操作を省略してもよい)。
- 得られたジアントラセンの約半量を、 外径16.5 mmのサンプル管に入れ、370 nmの励起光に対する蛍光の挙動を調べる。
- ホットプレート上で、加熱用のアルミブロックにサンプル管を入れ、 400 nm程度の波長のブラックライトを当てながら、 温度を300 °C程度まで上げて様子を観察し、 分解が終わったら電源を切り放冷する。
- ジアントラセン、および(6)でサンプル管に付着したジアントラセンの加熱生成物の 0.02 mg/mL程度のトルエン溶液を調製し、 ガラス製の光学セルを用いて紫外吸収スペクトルを測定する (300 nm以下の領域はガラスセルの吸収があるので測れない) 。
トルエンへの溶解度が低いので、ジアントラセン等の0.02 mg/mL溶液は、1 mg/5 mL程度の溶液を調製し、その0.5 mL(0.5 g)程度を希釈して5 mL(5 g)程度にすればよい。 ジアントラセンについては、300 nm~400 nmの紫外部に吸収が現れないことが、アントラセン2量体であることの証拠となることに注意する。 なお光二量化反応には少し純度の低い1級アントラセンを用いる。
【検討】
- ヒュッケル法による電子状態計算の結果から、 光二量化反応の生成物についてどのような説明が可能か考えてみよ。
注意
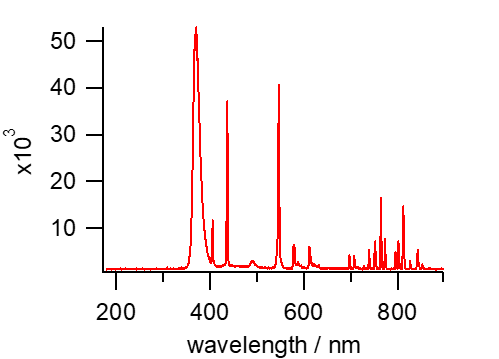
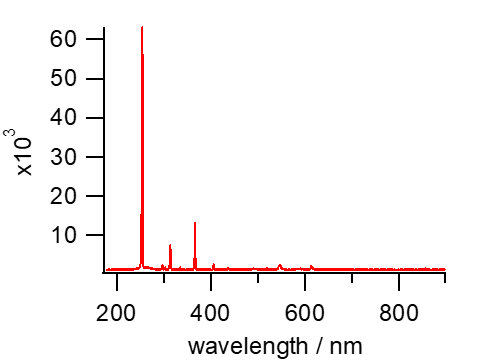
ジェルネイル用の紫外光源は、TLCのモニター用のブラックライトとちがって、 人体に有害とされる315 nm以下のUVB、UVC領域の光はほとんど出さない。 しかし図9に示すように400 nm以下の紫外線を、可視部よりはるかに強い強度で放射している。 一見光が弱いように見えても、直視したりしないように注意する。
|
|
| 図9. ジェルネイル用紫外線照射装置(右)とTLCのモニター用のブラックライト(左)の発光スペクトル。 | |
[付録] 単純ヒュッケル(Huckel)分子軌道法によるアントラセンの取り扱い
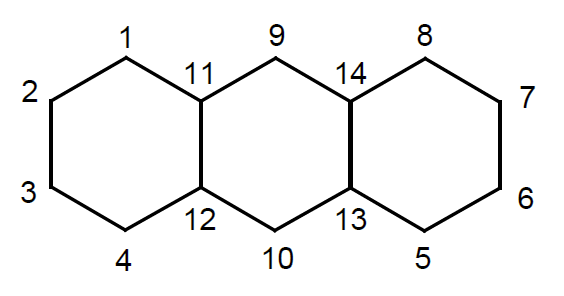
アントラセン分子のπ電子の状態が、 関連する14個の炭素原子の2p軌道の線形結合で与えられる分子軌道\(\Psi_i \)で表されるとする。
\begin{equation} \Psi_i = \sum_i {c_i | i \rangle} \label{eq:mo} \end{equation}
分子軌道\(\Psi_i \)はπ電子に対する有効ハミルトニアンを\(H\)とすると、
\begin{equation} H \phi_i = E_i \phi_i \label{eq:eigen} \end{equation}
で与えられるエネルギー固有値\(E_i\)に属する固有ベクトル (これを以下単に分子軌道と呼ぶ)\(\phi_i\)の線形結合で表され、 14個のπ電子はエネルギー固有値の小さい順に、分子軌道に入っていくものと考えられる。 ヒュッケル法(重なり積分を無視し、隣接する炭素原子以外の共鳴積分を無視) で与えられるアントラセンの分子軌道は表A-1のようになる。
| \(E_i^*\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| -2.414 | 0.21 | -0.15 | 0.15 | -0.21 | -0.21 | 0.15 | -0.15 | 0.21 | 0.30 | -0.30 | -0.37 | 0.37 | 0.37 | -0.37 |
| -2.000 | 0.29 | -0.29 | 0.29 | -0.29 | 0.29 | -0.29 | 0.29 | -0.29 | 0.00 | 0.00 | -0.29 | 0.29 | -0.29 | 0.29 |
| -1.414 | 0.28 | -0.12 | -0.12 | 0.28 | 0.28 | -0.12 | -0.12 | 0.28 | 0.40 | 0.40 | -0.28 | -0.28 | -0.28 | -0.28 |
| -1.414 | 0.17 | -0.41 | 0.41 | -0.17 | -0.17 | 0.41 | -0.41 | 0.17 | -0.24 | 0.24 | 0.17 | -0.17 | -0.17 | 0.17 |
| -1.000 | 0.41 | -0.20 | -0.20 | 0.41 | -0.41 | 0.20 | 0.20 | -0.41 | 0.00 | 0.00 | -0.20 | -0.20 | 0.20 | 0.20 |
| -1.000 | 0.00 | -0.35 | 0.35 | 0.00 | 0.00 | -0.35 | 0.35 | 0.00 | 0.00 | 0.00 | 0.35 | -0.35 | 0.35 | -0.35 |
| -0.414 | 0.31 | -0.22 | -0.22 | 0.31 | 0.31 | -0.22 | -0.22 | 0.31 | -0.44 | -0.44 | 0.09 | 0.09 | 0.09 | 0.09 |
| 0.414 | 0.31 | 0.22 | -0.22 | -0.31 | -0.31 | -0.22 | 0.22 | 0.31 | -0.44 | 0.44 | -0.09 | 0.09 | 0.09 | -0.09 |
| 1.000 | 0.00 | 0.35 | 0.35 | 0.00 | 0.00 | -0.35 | -0.35 | 0.00 | 0.00 | 0.00 | -0.35 | -0.35 | 0.35 | 0.35 |
| 1.000 | 0.41 | 0.20 | -0.20 | -0.41 | 0.41 | 0.20 | -0.20 | -0.41 | 0.00 | 0.00 | 0.20 | -0.20 | 0.20 | -0.20 |
| 1.414 | 0.17 | 0.41 | 0.41 | 0.17 | 0.17 | 0.41 | 0.41 | 0.17 | -0.24 | -0.24 | -0.17 | -0.17 | -0.17 | -0.17 |
| 1.414 | 0.28 | 0.12 | -0.12 | -0.28 | -0.28 | -0.12 | 0.12 | 0.28 | 0.40 | -0.40 | 0.28 | -0.28 | -0.28 | 0.28 |
| 2.000 | 0.29 | 0.29 | 0.29 | 0.29 | -0.29 | -0.29 | -0.29 | -0.29 | 0.00 | 0.00 | 0.29 | 0.29 | -0.29 | -0.29 |
| 2.414 | 0.21 | 0.15 | 0.15 | 0.21 | 0.21 | 0.15 | 0.15 | 0.21 | 0.30 | 0.30 | 0.37 | 0.37 | 0.37 | 0.37 |
問1.アントラセンの各炭素原子を(1, 4, 5, 8), (2, 3, 6, 7), (9, 10), (11, 12, 13, 14)とグループ分けすると、 計算される分子軌道の係数の大きさ\(|c_i|\)が等しいことを確認せよ。
問2.アントラセンの属する点群をD2とした時、 各原子軌道は規約表現で分類すると 3A1 + 4B1 + 3B2 + 4B3と表され、 指標表を用いて対称化軌道として次のような分子軌道を構成することができる。
| A1 | B1 | B2 | B3 | |
| σ1 | ([1] - [4] + [5] - [8])/2 | ([1] + [4] + [5] + [8])/2 | ([1] + [4] - [5] - [8])/2 | ([1] - [4] - [5] + [8])/2 |
| σ2 | ([2] - [3] + [6] - [7])/2 | ([2] + [3] + [6] + [7])/2 | ([2] + [3] - [6] - [7])/2 | ([2] - [3] - [6] + [7])/2 |
| σ3 | ([11] - [12] + [13] - [14])/2 | ([9] + [10])/21/2 | ([11] + [12] - [13] - [14])/2 | ([9] - [10])/21/2 |
| σ4 | ([11] + [12] + [13] + [14])/2 | ([11] - [12] - [13] + [14])/2 |
異なる規約表現に属する分子軌道\(\Psi_a\)と\(\Psi_b\)について\(\langle \Psi_a | \Psi_b \rangle\)、 \(\langle \Psi_a | H | \Psi_b \rangle\)が0になることを確認せよ。 またA1の対称性に属する対称化分子軌道を用いて永年方程式を構成し、 エネルギー固有値を計算せよ。 余裕があれば、他の対称性に属する対称化分子軌道についてもエネルギー固有値を計算してみよ。