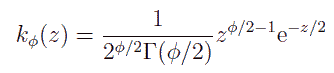
標準正規分布 N(0, 1) に従う確率変数 {xi} において、そのφ個について2乗をとって足し合わせた変数 z を考えます。
この変数 z の従う確率分布をカイ2乗(χ2)分布と呼びます。 カイ2乗分布の確率密度関数 kφ(z) をあからさまに書くと次のようになります。
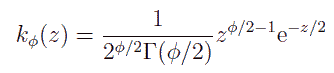
ここで Γ はガンマ関数です。 カイ2乗分布はまた、次のような漸化式で与えることもできます。
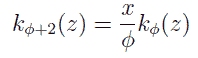
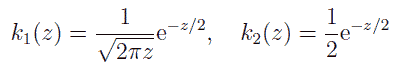
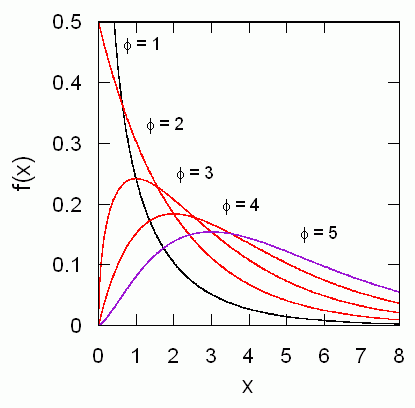
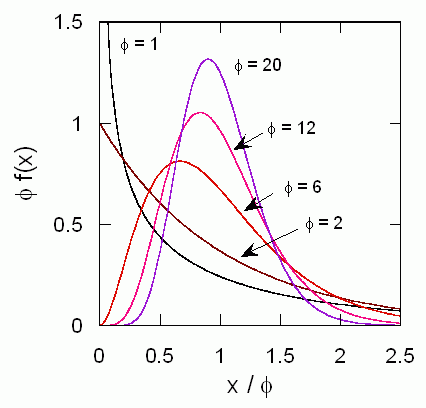
カイ2乗分布は、自由度の増加とともに図4に示すように変化します。 自由度 φ のカイ2乗分布に従う変数 z の平均は φ、分散は 2φ になります。
すでにお気づきのことかもしれませんが、自由度3のカイ2乗分布に相当するものは、マクスウェルの速度分布としてすでにおなじみのものです (よりなじみの形にするには z = v2 という変数変換が必要ですが)。 一般の M 粒子系の運動エネルギーのカノニカル分布は、自由度 3M のカイ2乗分布を用いて表されます。
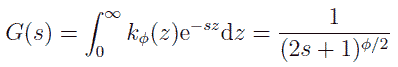
偏差が正規分布に従うなら、偏差2乗和を分散 σ2 で割ったものは自由度 N - 1 のカイ2乗分布に従います。 このことは線形代数で学んだであろう手法を用いて、以下のようにして示すことができます。
確率変数 {xi} は互いに独立で、平均 0 分散 1 の標準正規分布に従う (=元のデータが正規分布に従うものとして、2章で見た標準化を行った)ものとします。 また内積 (u, v) を次のように uv の平均で定義します。
内積 (xi, xj) は i = j の時 1 で、i ≠ j だと 0 です(={xi} は正規直交基底になっている)。 さて偏差2乗和は xi の2乗の和から、標本平均の2乗の N 倍を引いたものです。
ベクトル {xi} に線形変換を施して、この式を正規直交ベクトルで書き直してみます。 ここではあまり抽象的にならないように、具体的にシュミットの直交化法を適用した計算を示しましょう。
まず m を規格化したベクトル z1 は下記のようになります。
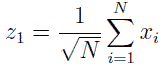
この z1 に直交する成分を x1 から切り出します。
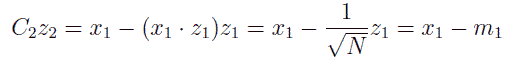
ここで C2 は規格化のための定数で、mj は次式で定義される量です。
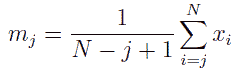
mj は N - j + 1 個のデータに対する標本平均と見てもらえればよいでしょう。 また C2 は下式で与えられます。
もう少し計算を示しましょう。 z1 と z2 に直交するベクトル z3 をx2 から作ると次のようになります。
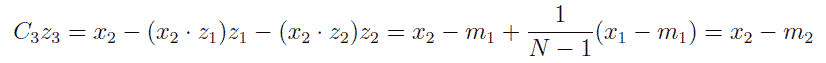
C3 は下式で与えられます。
こうした操作を続けていくと、次のような規格直交化されたベクトルの組が得られます。
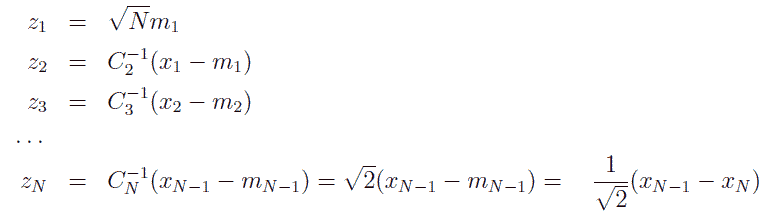
規格化の因子 Cj は下式で与えられます。
こうして決めた正規直交基底 {zi} を用いて、偏差2乗和 S は次のように書き下せます
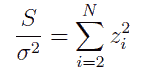
ここで zi という変数はいずれも独立で平均が 0、内積が 1 の標準正規分布に従います(正規分布に従う変数の和も正規分布に従う)。 ですから偏差2乗和は自由度 N - 1 のカイ2乗分布に従うことになります。
標本分散の確率分布という立場からは、偏差2乗和を N - 1 で割ったものを考えることになります。 図5にこうした観点からカイ2乗分布を書き直した、標本分散の確率分布を示します。 すでに5章でも触れましたが、データ数が10個ぐらいであれば標本分散には5割近い不確定さを、 20個でも3割ぐらいの不確定さを覚悟しておかないといけません。 標本標準偏差であれば、推定の精度はこの2倍程度よい(10個ぐらいで2割強の不確定さ)わけですが、そんなに大きく違うわけではありません。 数個のデータから標本分散を算出しても、そこにはきわめて大きな不確定さをともなうことをよくよくご理解ください。
なお上式から明らかに、偏差2乗和(そして標本標準偏差 s)は標本平均 m と統計的に独立です。 標本平均 m の誤差を標準偏差で評価すれば σ/N1/2 です。 この標準偏差 σ を標本標準偏差 s で置き換えて議論しても、そんなに的外れではないのですが、 ここまでで見たように標本標準偏差には大きな不確かさがともないます。 そこで次のような確率変数 y を考えてやることで、より精度の高い標本平均の不確かさの推定が可能となります。
この確率変数 y は、標準正規分布に従う確率変数 (m - μ)/[σ/N1/2] を、 それと独立な(平均が 1 になるように標準化した)自由度 N - 1 のカイ2乗分布に従う変数 s2/σ2 の平方根で割った形になっています。 これ以上の立ち入った話はやめておきますが、 この確率変数 y の従う分布を t-分布(Student 分布。Student は統計学者 W. Gosset のペンネーム)と呼び、関連の数表なども整備されているところです。