このおはなしは、3回生の物理化学・物性化学実験 B3 に関わって用意した解説プリントを、 HTML 化したものです。
データから種々のノイズを除く手法は、オーディオや画像処理では、イコライザーやローパスフィルターのような形で日常的にもよく出会うところです。 ここでは今回の実験で出会う(出会った)いくつかの手法について、簡単に触れておきます。 なおデータとして等間隔のデータ \(\{x[i]\}, i = 1, 2, \ldots\) を想定します。
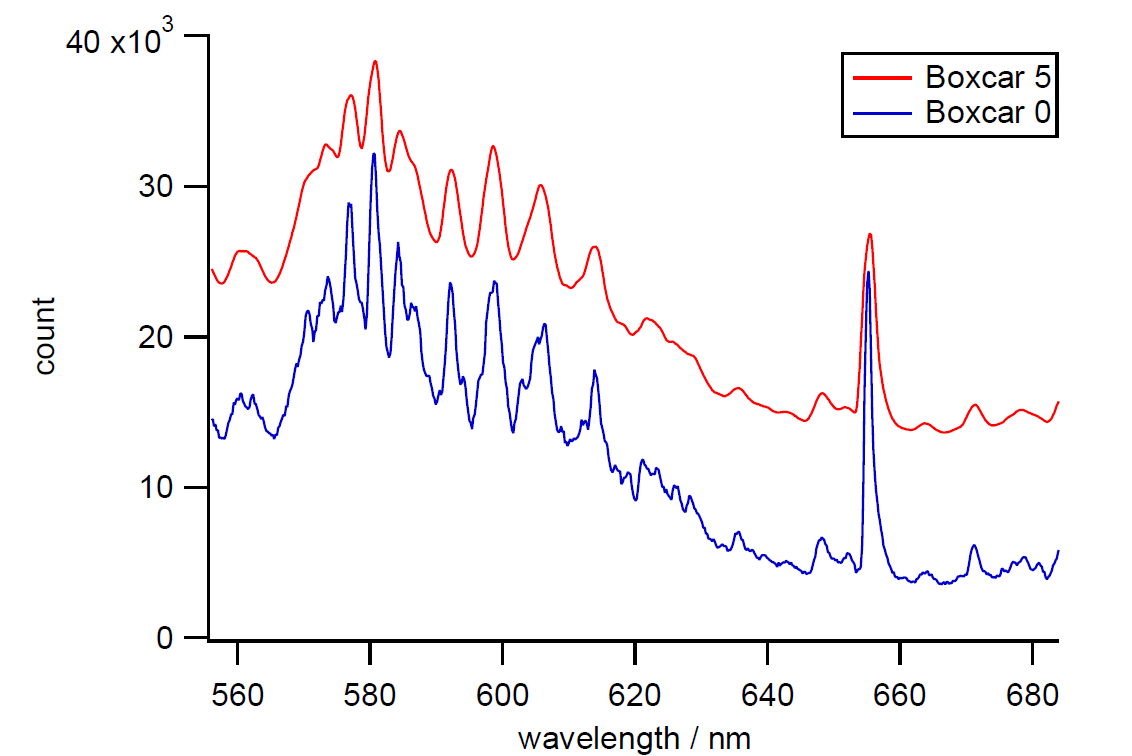
中には何も考えずに設定していた人がいるかもしれませんが、CHEMUSB4 の分光光度計を使う時、 Spectra Suite で Boxcar の設定を 5 にするように指示されていました。 この設定をすることでスペクトルが滑らかなものになったと思います。 CHEMUSB4 では受光素子がおよそ 0.2 nm 間隔で光の強度を検知するように配置されおり、 Boxcarの設定を 5 にすると、対象の受光素子の周辺の 5 個分の素子の平均を出力することになります。

|
| 図 1. Spectra Suiteで得られた光源の強度スペクトル。 赤はBoxcarを5に設定した場合で、重ならないよう少し上方にシフトしてある。 |
この手法はノイズを除くたぶんもっとも簡単な手法で、 奇数個 \(2N+1\) 個の平均を取る設定にしておくと、元のデータ \(\{x[i]\}\) から作られる平滑化したデータ \(\{y[i]\}\) は次のような式で表されます (両端末のデータの処理についてはここでは無視):
\begin{equation} y[i] = \frac{1}{2N+1} \sum_{n=-N}^N {x[i+n]} \label{eq:filt1} \end{equation}
実際に計算する上からは、順次、次のような計算をすることで \(\{y[i]\}\) は求められ、 通常「移動平均 moving average」と呼ばれます。
\begin{equation} y[i+1] = y[i] + \frac{x[i + N + 1] - x[i-N]}{2N+1} \label{eq:filt2} \end{equation}
こうして処理した結果を見ると、図 1 に見るように元のデータのギザギザが減って、滑らかなスペクトルになっていることが分かります。 しかし同時に例えば 656 nm 付近の輝線に注目すると、 元の鋭いピークが、幅の広い鈍いものになっています。 というところで、ギザギザ(ノイズ)を減らしつつ、大事な情報はできるだけ残したいというので、 いろんな手法が開発されてきました。 化学でよく出会うのは、ある重み \(\{w[n]\}\)をかけた平均を取る手法です。
\begin{equation} y[i] = \frac{\sum_{n=-N}^N {w[n] x[i+n]}}{\sum_{n=-N}^N {w[n]}} \label{eq:filt3} \end{equation}
化学で伝統的によく行われてきたのは、元のデータ \(\{x[i]\}\) を \(i\) の近傍で多項式
\begin{equation} f[i+n] = a_0 + a_1 n + a_2 n^2 + \cdots \label{eq:polyfilt1} \end{equation}
に最小2乗法で当てはめる手法です(\(n = -N, \ldots, N\)。米国などでは Savitzky-Golay 法と呼ばれる)。 かりに 3 次式に当てはめるとすると、次のような正規方程式を解くことになります:
\begin{equation} \left( \begin{array}{ccc} S(1) & S(n) & S(n^2) & S(n^3) \\ S(n) & S(n^2) & S(n^3) & S(n^4) \\ S(n^2) & S(n^3) & S(n^4) & S(n^5) \\ S(n^3) & S(n^4) & S(n^5) & S(n^6) \end{array} \right) \left( \begin{array}{c} a_0\\ a_1\\ a_2\\ a_3 \end{array} \right) = \left( \begin{array}{ccc} S(1) & 0 & S(n^2) & 0 \\ 0 & S(n^2) & 0 & S(n^4) \\ S(n^2) & 0 & S(n^4) & 0 \\ 0 & S(n^4) & 0 & S(n^6) \end{array} \right) \left( \begin{array}{c} a_0\\ a_1\\ a_2\\ a_3 \end{array} \right) = \left( \begin{array}{c} S(x[i+n])\\ S(n x[i+n])\\ S(n^2 x[i+n])\\ S(n^3 x[i+n]) \end{array} \right) \label{eq:polyfilt2} \end{equation}
ここで \(S(Q(n))\) は \(Q(n)\) の \(n\) についての和
\begin{equation} S(Q(n)) = \sum_{n=-N}^N {Q(n)} \label{eq:polyfilt3} \end{equation}
を表します。式 \eqref{eq:polyfilt3} を解いて得た係数 \(a_0\) が平滑化された値 \(y[i]\) というわけで、 結果的には式 \eqref{eq:filt3} のような \(x[i-N], x[i-N+1], \ldots , x[i+N]\) にある重みをかけて足しこんだものになります (\(a_0\) だけに注目するなら、当てはめに使用する多項式が2次式でも3次式でも同じ結果になることに注意)。 また \(a_1\)、\(a_2\) 等から微係数の値も得られ、esr 等のシグナルの解析などに有用です。 種々の多項式の次数、当てはめ範囲 \(N\) について得られた重みの表も与えられています (Savitzky and Golay)。 たいていの科学技術用のソフトにはこうした平滑化の処理は組み込まれており、無論 Igor にも入っています。
平滑化の手法としてより一般的なのは、高周波数成分を取り除くなど、 フーリエ変換などの際に用いられる種々の技法です。 皆さんが目にしている Cary 630 の赤外スペクトルは、得られた干渉パターンのフーリエ変換で得られているわけですが、 フーリエ変換にともなうノイズを減らすため同様に平滑化を行っています (この道ではアポダイゼーション Apodization と呼ぶ。今回の実験では Happ-Genzel 関数を使用)。 こうした世界での手法と深くかかわって、最近では2項フィルター binomial filter を使うのが一般的になってきているようです。 2項フィルターでは重み関数として2項係数を用います:
\begin{equation} y[i] = 4^{-N} \sum_{n=-N}^N {{}_{2N} \mrm{C}_{N+n} x[i+n]} \label{eq:binom} \end{equation}
無論この処理も Igor に入っていて、Igor で平滑化処理を選択するとまず Binomial が出てきます (メニューの「Analysis」から「Smooth…」をやってみてください)。 2項フィルターは \(N\) が大きくなるとガウス型のフィルターになります。
|
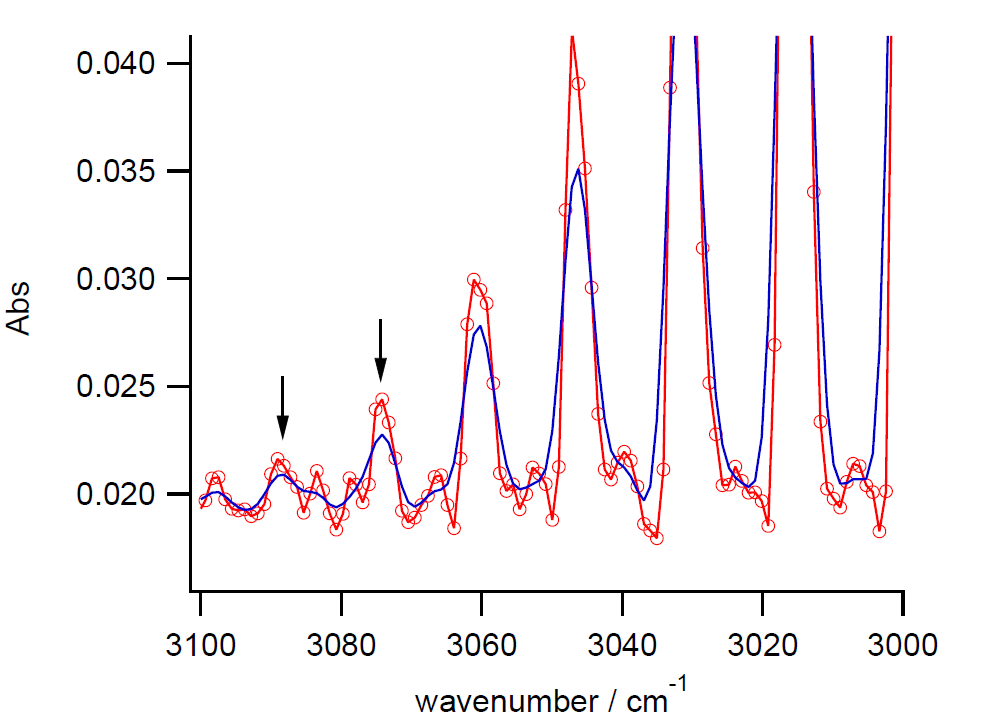
| 図 2. HClの振動回転スペクトルに平滑化を施した例 (Binomial smoothingを5に設定。青線) |
実際にこの平滑化処理を施した赤外スペクトルの例を図2に示します。 先の図1でも見たように、ピークの幅が広がり、判別しにくくなっている面もありますが、矢印で示したピークのように、 生のデータではノイズと区別するのが難しそうなピークもそれなりにピークとして表れてきているように見えます (分光のプロはこんなことをしなくても ”心眼” でピークが見えるらしい・・・)。
このようにノイズの中からシグナルを取り出す上で、こうしたデータ処理は大変有用です。 ただしまず何より重要なのは、ノイズの少ない、質の高い生のデータを取ることであることは、 心しておいていただきたいところです。