2値データ (x,y) を拡張して、測定値 y が m-1 個の変数 x(1), x(2), ・・・, x(m-1) に依存する場合に、
y = a0 + a1 x(1) + a2 x(2) + ・・・ + am-1 x(m-1) (16)
なる線形の式を、測定して得られる N 個のデータに、もっとも、もっともらしく当てがう事を考えましょう(x(0) = 1 と考えます)。これは、たとえば m-1 個の変数として、2値データ (x, y) について、(x, x2, x3, ・・・, xm-1)をとれば、実験結果の多項式への当てはめの問題ということになります。
以下、表記を簡単にするために、Tx = (1, x(1), x(2), ・・・, x(m-1)) を用い、(16)式を
y = Tx a (17)
と書き、またそれぞれの測定値の分散は同じで s02 とします。ここで Tz は z を転置したものです。
さて1章と同じような考察から、
![]() (18)
(18)
を最小にするような a をとれば、もっとも、もっともらしいパラメーター a が決まります。ここから得られる正規方程式は次のようになります。
![]()
![]()
・・・・・・・・・
![]() (19)
(19)
これはコンパクトに次のように表記できます。
TX X a = TX y (20)
ここで X は、N 行 m 列の行列で、Xij は xi(j-1) に相当し、 y は観測値 yi を成分とするベクトルです。この(20)式から、最適のパラメーターは次式によって得られます。
a = (TX X)-1 TX y (21)
☆クロメル-アルメル(CA)熱電対の起電力は0~100 ℃の範囲でかなりよい直線性を示すが、わずかに非直線性がある。下に示すデータを用いて、0~100 ℃でのCA熱電対の熱起電力を温度 t の2次関数で表現してみよ。
| t /℃ | V / mV | t /℃ | V / mV | t /℃ | V / mV |
|---|---|---|---|---|---|
| 0 | 0.000 | 40 | 1.611 | 80 | 3.266 |
| 10 | 0.397 | 50 | 2.022 | 90 | 3.681 |
| 20 | 0.798 | 60 | 2.436 | 100 | 4.095 |
| 30 | 1.203 | 70 | 2.850 |
3章では、a を変動させたときの偏差の変動を考えたわけですが、ここではもっと直接的に、a 自身が測定データの誤差とどう関わっているかを考えることにしましょう。(21)式から、測定値 y に dy だけの変動がある時、決めた、もっとも、もっともらしいパラメーター a(0) の変動 da は
da = (TX X)-1 TX dy (22)
で評価されます。したがって、推定パラメーター a の共分散行列の期待値は
E [da dTa] = E[(TX X)-1 TX dy dTy X (TX X)-1]
= (TX X)-1 TX E[dy dTy] X (TX X)-1
= s02 (TX X)-1 (23)
で与えられる(E[dyidyj] が、i≠jの時 0、i = j の時 s02となることに注意)。つまりそれぞれのパラメーターの分散は次のように評価できるわけです。
E [(daij)2] = s02 (TX X)-1ij (24)
次に問題になるのは s02の評価ですが、(15)式のように
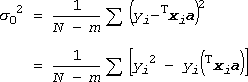 (25)
(25)
で評価する事ができます(付録A)。
☆m = 2 のとき、(13)、(14) 式が導出できることを確かめよ。
☆CA 熱電対の起電力を与える式のパラメーターの誤差の評価を行え。
ここまでもっぱら、すべてのデータの分散が等しい( s12 = ・・・ = sN2)として標式を導いてきました。しかし取り扱うデータによっては、それぞれのデータの信頼性が異なる場合があります。たとえば、かりに相対誤差が x に反比例するようなデータを扱うならば、 s12 x12 = ・・・ = sN2 xN2、という関係を導入する必要があります。
こうしたデータごとに信頼性がちがうデータを扱う場合には、それぞれのデータにwi ( = s02/si2) だけの重みをつけて
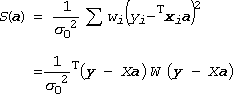 (26)
(26)
を最小にするという形で問題を設定すればよい。ここでWは対角成分Wii = wi の対角行列。また s02 は標準的な測定(=重みが1)に関わる分散です。これから得られる正規方程式は次の形に書けます。
TX W X a = TX W y (27)
だからもっとももっともらしいパラメータは
a = (TX W X)-1 TX W y (28)
で与えられます。またその分散の期待値は、次式で評価されます(W = E[dy dTy] に注意する)。
E [(dai)2] = s02 (TX W X)-1ij (29)
そして標準的な測定の分散 s02 は、次式で評価されます。
![]() (30)
(30)