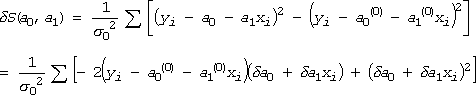もっとも、もっともらしい直線関係の式をえたわけですが、ではそれは、どれぐらいもっともらしいのでしょうか？いくつか考え方があるでしょうが、たぶん一番考えやすいのは、引いた直線を少しずらしてみた時、どれくらい偏差が大きくなるかということでしょう。そういった立場から、少し考えてみることにします。

a₀ = a₀⁽⁰⁾ + da₀, a₁ = a₁(0) + da₁ というパラメーターの微小な変動を考えます。ここで a₀⁽⁰⁾、a₁⁽⁰⁾ は前章で決めた最適値を表わすものとします。この時、先の S(a₀, a₁) の変動は次の式で与えられます。

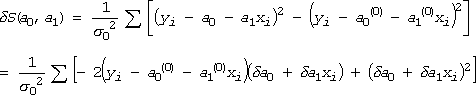　　(10)

ここでs₁² = ･･･ = s_N² = s₀²とおきました。 (10)式 ２段目の式において、[ ] 内の第１項は正規方程式から 0 になり、結局次 式となります。

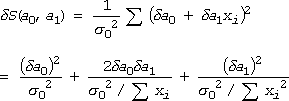　　(11)

つまり、最小２乗の条件が満たされる時、決定したパラメーターの“もっともらしさ”に対する分布は、２次元の正規分布に従うわけです。もう少しあからさまに書けば

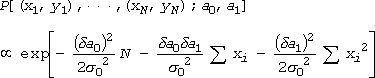　　(12)

と表現できることになるわけです。(12)式から、a₀、a₁ の分散を求めると次のようになります。

　　(13)

　　(14)

なお da₀ と da₁ は独立ではないので、分散の取扱いには注意が必要です（付録Ｂ参照）。ここで問題は y の分散 s₀² になるわけですが、これは最適化した直線からのはずれぐあいから、

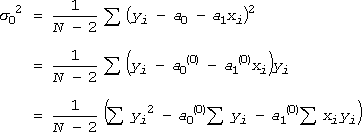　　(15)

で評価できます。（付録Ａ参照）

☆前章で取り上げた例について、上の手法でパラメーターの誤差を評価してみよ。