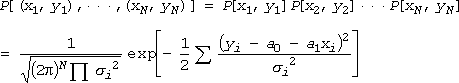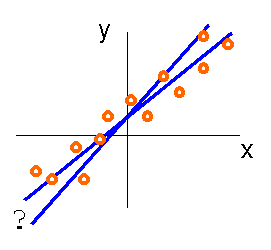
２値データ (x, y) を考え、x を変化させて y の値を測ったとします。この時、次の仮定が満たされているものとしましょう。

(i) 測定は独立に行なわれ、測定値 y のばらつきは正規分布に従う。

(ii) 本来、測定値は
　　　y = a₀ + a₁x　　(1)
　　なる法則に従う。

こうした時、得られた一連のデータ、 (x₁, y₁), (x₂, y₂), ・・・, (x_N, y_N) をグラフにプロットして、それらの点から得られる、もっとも、もっともらしい直線関係は、どういうものでしょう？またそれは、どれぐらいもっともらしいのでしょう？

一連のN個の観測値 (x₁, y₁), (x₂, y₂), ・・・, (x_N, y_N) に注目します。互いに独立で正規分布に従うのですから、このN個のデータが出現する確率 P[(x₁, y₁), ・・・, (x_N, y_N)] は次式で表現できます（以下、S は i = 1 から N までの総和を表わすものとします）。

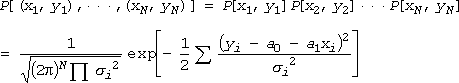　　(2)

だから、N 個のデータからもっとも、もっともらしいパラメーター、a₀、a₁ を決めるには、

　　(3)

を最小にするように、a₀、a₁ を取ればよいのです。つまり偏差の２乗を最小にすればよいわけで、この偏差の２乗の和を最小にするようにパラメーターを選んで、もっともらしい直線を引く方法を、最小２乗法(method of least squares)と呼びます。