窒素を加えるとアンモニアが分解する？

窒素と水素からアンモニアが生成する、化学平衡を考えます：

N₂ + 3H₂ ⇌ 2NH₃

この反応はルシャトリエの原理の適用例として、高校の教科書にもよく登場します。

先生： 圧力をかけると、この反応の平衡はどちらに移動しますか？

生徒： ハイ！圧力をかけると体積が小さくなる方向に平衡が移動しますから、分子数が少なくなって体積が小さくなる方向。つまりアンモニアが生成する方向に平衡が移動します。

先生： そのとおり！よくできました。さてここに、アンモニアを加えました。平衡はどちらに移動しますか？

生徒： ハイ！アンモニアを減らす方向、つまり加えたアンモニアが分解する方向に平衡が移動します。

先生： そのとおり！よくできました。・・・・・

といった具合です。でも、この反応について、こんなこと考えてみた事ありますか？
(以下ではお話を簡単にするために、気体の非理想性、つまり理想気体の状態方程式からのはずれは無視できるものとして議論することにします。)

何もまちがった式を立てているわけではありませんよね？
ルシャトリエの原理には、こうした例外があるんですよ・・・。？？？

　この問題、みなさんはどう考えますか？
　ぼくの考えを紹介する前に、同じようで、ちょっとちがう問題の展開をしてみましょう。分圧で考えてみるのです。

さっきと今と、どこがどうちがうのでしょう？

もうお気づきでしょうか？あからさまには書いていませんが、モル分率表示で考えた時は、反応は全圧力一定で考えていました。 分圧表示で考えた時は、体積一定で考えていました。ここの所に、２つの問題の設定のちがいがあります。

モル分率表示で書いた時、体積一定の条件であったなら、窒素を加えたら全圧が変化し、平衡定数 K_x の値が変わったはずです。 また分圧表示で書いた時、全圧一定の条件であったなら、窒素分圧が上がった分だけ、水素とアンモニアの分圧が下がったはずです。 この効果をどう取り扱うかで、議論は変わってしまうのです。

不活性ガスがあったなら・・・

ここまでの話では窒素、水素、アンモニアだけしかないので、話がいささかやっかいでした。 ここに不活性ガスのアルゴンが n_i mol 入っていたと考えてみてください。さっきの式は

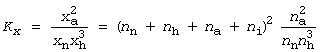
となり、アルゴンが十分たくさんあれば（n_i » n_n, n_h, n_a）、

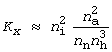
となります。

この状態で窒素を加えれば、平衡はアンモニアが生成する方向に移動します（ルシャトリエの原理が成立！）。 また、アルゴンをさらに加えれば、平衡はアンモニアが分解する方向に移動します。 アルゴンを加えるのは、反応混合物を希釈することですから、平衡は分子数を増す方向に移動する。これもルシャトリエの原理の教えるところです。

モル分率表示の複雑な内実

モル分率表示で考えるということは、全圧が一定ということを、言外に意味していました。そして、全圧が一定の下で窒素を加えるということは

ことでもあったわけです。

モル分率表示の平衡定数を持ち出してルシャトリエの原理を適用する時、この①にアクセントを置けば、平衡はアンモニア生成の方向に、②にアクセントを置けば、平衡はアンモニア分解の方向に移動する。 ルシャトリエの原理だけからは、明確な答えは得られないのです。 ですから、この一方だけを声高に主張して、ルシャトリエの原理の当否を問題にするのは、お門違いの感があります。

さらに言うと、モル分率で表した平衡定数は、分圧や容量濃度で表した平衡定数と違って次元を持たないので、 より透明な内実を持っているような印象を与えるのですが、その見かけに惑わされてはいけません。 モル分率で表した平衡定数は、容量濃度で表した平衡定数よりも、より複雑な内実を持っているのです。このあたりのお話は、また別の機会に考えてみることにしましょう。

「ルシャトリエの原理の暗い部分」へ返る