|
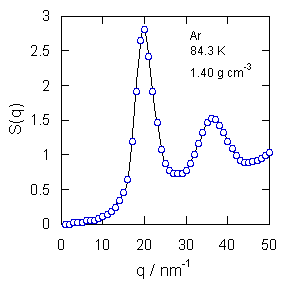
| 回折実験の模式図(右)と、X線回折実験による構造因子の例(左)。 なおX線回折実験では構造因子を求める際、入射強度と回折強度の比 I(θ)/I0 から、各原子内での回折による寄与(原子散乱因子)を取り除く。 |
液体中で分子はでたらめな配置を取っていると考えてよいのですが、反発力が働いてある距離以上には近づけないなど、近傍の分子の配置との間には何らかの秩序が存在するはずです。 このことは実験的にはX線や中性子線の回折実験から分かっています。 入射した中性子線の、ある角度 θ への散乱強度を調べると、図のようなパターンが得られます(構造因子と呼びます。 ここで Q = (4π/λ) sin(θ/2)で、λは中性子線の波長、θは散乱角)。


|
| 回折実験の模式図(右)と、X線回折実験による構造因子の例(左)。 なおX線回折実験では構造因子を求める際、入射強度と回折強度の比 I(θ)/I0 から、各原子内での回折による寄与(原子散乱因子)を取り除く。 |
これは液体中に何らかの構造があることを示していて、ここからある分子の周りの分子の分布の様子を推定することができます。
原理的には分子間の相互作用がわかっておれば、温度・密度を与えたときにどのような液体構造が現れるかは予測できるはずなのですが、 パチンコ玉のような剛体球からなる流体についてでさえ、これはたいへん難しい問題です。 そのためモデル物質を用い、ゼラチン球の懸濁液を作り、ゼラチン球間の距離の出現確率を調べるといった研究もかっておこなわれました 。
現在では計算機実験(シミュレーション)を用いた研究によって、液体の構造と分子間相互作用の関係についていろんな知見がえられるようになってきました。 中でも単原子液体については、液体中の分子の分布が、剛体球分子のからなる流体の分布でうまく表現できるということは重要な発見でした。 このことは液体の構造の骨格が分子間斥力で作られていることを示すもので、液体の示すさまざまな現象に対する今日的な解釈の基礎になっています。