a mol の A と b mol の B から c mol の C ができる化学反応を考えましょう。 この反応の反応進行度を z とすると、それぞれの物質量は nA(t) = nA(0) - az, nB(t) = nB(0) - bz, nC(t) = nC(0) + cz と表すことができます。 この反応の反応速度は反応進行度の時間変化率 dz/dt で定義され、平衡状態では反応速度は 0 になります。 平衡定数は、平衡状態における各成分の濃度の間に成り立つ関係を表わします。 溶液中の反応にはさまざまな類型があり、たとえば食塩の結晶の溶解も見方によっては、結晶中の Na-Cl のイオン結合が切れて新たに水分子との相互作用が形成されるという化学反応です。 ここではいくつかの典型的な液相中の化学平衡と反応速度の問題を取り上げます。
温度を上げた時、酸解離定数は大きくなることもあるし、小さくなることもあります。 十分温度が低い時、温度を上げるにしたがって酸解離定数は大きくなり、温度を上げるにつれ減少に転じます。 低温で吸熱反応であったものが、高温で発熱反応に転じると見ることもできます。
この挙動は結合エネルギーと溶媒の誘電率の温度依存性から説明することができます。 酸が解離する時に必要なエネルギーを、溶媒の性質に鈍感な共有結合のエネルギーと、溶媒の性質に強く依存する静電的な相互作用からなるとしましょう。 静電的な相互作用は誘電率に反比例すると考えることができますから、温度を上げていくと誘電率が減少し、あるところで解離がエネルギー的に不利になると考えるわけです。
溶液中のイオン会合では共有結合の要素が小さいので、もっぱら静電的な効果が現れ、温度を上げると、イオンはより会合しやすくなります。 たとえば食塩は 1740 K で沸騰しますが、その蒸気中で食塩はおもにNaClという分子として存在しており電離はほとんど起きていません。 さらに温度を上げていくと、熱エネルギーが優勢になる領域に達し、再びイオンへの解離が起きるようになりますが、それにはさらに数千 K 以上の温度が必要になります。
温度依存性で見た変化は、圧力の効果、体積変化の観点から見るとより明瞭に見えてきます。 塩酸と水酸化ナトリウム溶液を混ぜて中和した時、およそ 20 cm3 mol-1 体積が増加する (水 1 molの体積は 18 cm3 mol-1 です)ことが知られています。 これは圧力をかけると誘電率が大きくなり、イオンがより安定化されるためです。 あるいはイオンの周りに強く水和していた水分子が解放されるためだと考えることもできます。 ですから同じ中和反応でも、アンモニア水で塩酸を中和する時には、逆に体積の減少が起きます。
一般にイオンを含む溶液に電解質を加えると、イオンが安定化されます。 大まかに言って、この安定化の度合いは注目するイオンの電荷の2乗 z2 に比例し、溶液のイオン強度 I の平方根に比例することが知られています。 イオン強度というのは、溶液中に存在するすべてのイオン種について、電荷の2乗と濃度の積をの和を取ったものです:
![]()
酢酸など中性の酸の電離について考えると、イオン強度が大きくなるほど、電離するのが有利になり、酸解離定数は大きくなります。 一方、アンモニウムイオンが解離する
NH4+ ⇔ NH3 + H+
という平衡では、塩を添加しても平衡はほとんど変化しません。
液相が水相と油相に分離している場合、溶け込んだ溶質は水相・油相にある比率で分配されます。 この水相と油相への分配比はほぼ一定(分配則、あるいはネルンストの法則と呼ばれることもある)で分配係数と呼ばれます。 ガスクロマトグラフィーや高速液体クロマトグラフィーでは、しばしばこの相間の溶質の分配が利用されます。
ところが酢酸や安息香酸などカルボン酸の分配平衡については、水相の濃度の2乗と油相の濃度の比がほぼ一定であることが知られています。 これは酢酸や安息香酸などが油相では主に二量体として溶存しているためとして解釈できます。 たとえば酢酸の蒸気中では酢酸分子は大部分二量体として存在していることが知られています。 同様の現象は水相・油相の分配に止まらず気相・液相でも見られ、おそらく塩酸はもっともよく知られた例です。 会合が次々と進行し、いわゆる会合性コロイド、ミセルなどが形成される場合もあります。
先に6.2節で、対流や分散の効果がなければ、コップの中で砂糖が拡散して均一になるのに半年かかることを見ました。 同様に溶液中での化学反応速度を考えるうえでも、拡散の問題は避けて通れません。
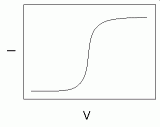
拡散の問題がもっとも顕著に現れるのは、おそらく電気分解においてでしょう。 直径が 10 μm 以下程度の微小な電極を負極にして溶液の電気分解を行うと、電圧を徐々に変化させていった時、図のような電流の変動が現れます。 電流値が急速に増大するのは、溶液中に溶けている酸化剤の還元が起きはじめる電圧です。 そしてある電流値に達すると、電圧を大きくしても電流値の増加は認められなくなります。 この電流が頭打ちになる現象は電極付近の酸化剤濃度がほぼ 0 になり、溶液中からの拡散による酸化剤の供給が全体の速度を決めていること、律速段階になっていることを意味しています。 この電流値を限界電流と呼び溶液中の酸化剤濃度に比例することが知られています*。
* このことを利用した分析法をボルタンメトリーvoltammetry(volt + ampere)、特に水銀を滴下して電極とするものをポーラログラフィーpolarographyと呼びよく研究されています。なお電極の形状や大きさ、あるいは溶液の撹拌などによって電極近傍の溶質の拡散のようすは大きく変化し、それに応じてさまざまな限界電流の表式が与えられています。
系がほぼ均一になってしまったとすると、拡散の問題はもはやあまり大きな問題にはなりません。 先に考えたように、拡散に要する時間は、注目する距離の2乗に比例するとみることができます。 ですからほぼ数 nm スケールまで均一になった溶液中では、数 cm オーダーの不均一さをならすのに要する時間の 10 の 14 乗分の 1、百兆分の 1 で拡散の過程は終わってしまいます。
ですから通常、人間にとって意味のある時間スケール(数秒~数時間)でおきる均一相の化学反応の律速段階はたいていの場合、反応に関与する分子の複合体が周りの分子からエネルギーを受け取って化学変化を起こす過程です。
A + B → AB* → C
化学反応の遷移状態理論といわれるものは、反応の中間のもっとも不安定な状態AB*(遷移状態)の分解する速度を kBT/h で評価しようとするもの(ここで h はプランク定数と呼ばれる定数で 6.63×10-34 J s)で、反応速度定数は
![]()
で与えられます。ここで K は反応物 A、B と遷移状態 AB* の間の平衡定数に相当し、反応速度の問題を化学平衡の問題に帰着させることができます。 この取扱いは多くの反応で成功を収めてきました。 塩効果についての研究はその典型的な例です。
仮に電荷が z1 と z2 の分子種 X と Y が反応したとしましょう。 このとき遷移状態の電荷は z1 + z2 になりますから、イオン強度 I による効果は
![]()
より、z1z2に比例することが期待されます。 実験的にもこのことは多くの系について検証されています*。
*溶液中に2価のイオンがある場合などはイオン対などが生成し、この単純な関係から外れることが知られています。