|
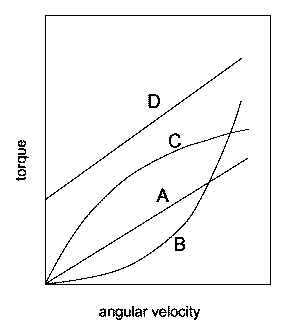
回転速度と偶力の関係。 A: ニュートン液体 B: ダイラタンシー C: 擬塑性流体 D: ビンガム塑性流体 |
液体の粘さがものによってさまざまであることは皆さんよくご存知でしょう。 けれどもいざ粘さを表現しようとすると厄介です。
粘さは液体を流動させた時に現れる抵抗力といえるでしょう。 けれども抵抗力の内実は液体の流れの様子によって変化します。 たとえば抵抗力の中には、摩擦力でない部分があります。 風呂の湯の中で手をさっと動かしてみてください。 手には抵抗力が働きます。 ところでその手を急に止めたらどうでしょう。 手を最初に動かしていた方向に動かすように力が働くのが感じられるでしょう。 「摩擦力」であれば、常に運動と反対方向に働くはずです。 これは手とともに周りの水が動く効果、実質的に質量が増加したようにふるまう効果を反映しています。 また流れが安定でなく時々刻々渦が生まれ消えていくような場合には、液体を構成する物質よりは、むしろ流れの性質が本質的に重要になってきます(乱流)。 このような効果を取り除くには、等速運動で乱れのない定常的な運動を扱って考えてみればよいでしょう。 これは外部から加えたエネルギーが運動のようすを変えることなく熱に変わっていく過程を見ることに相当します。
液体の中に棒を差し込んで、棒を一定速度で回転させた場合に働く力で粘さを測ることにしましょう。 では回転速度とその時に受ける抵抗力(偶力)の間には、どんな関係が成り立つでしょうか? 液体の種類によって、そのパターンはいささか異なります。

|
回転速度と偶力の関係。 A: ニュートン液体 B: ダイラタンシー C: 擬塑性流体 D: ビンガム塑性流体 |
水やトルエンなどの場合は回転速度に比例して抵抗力が変化します(ニュートン流体と呼びます)。 けれども歯磨きのペーストやクリームなどでは回転速度が 0 でも抵抗力が現れ、ある程度の偶力を与えて始めて棒が回り始めます(ビンガム Bingham 塑性流体)。 またよく似た挙動ですがペイント液などでは回転速度を上げると抵抗力の増加量が減っていきます(擬塑性流体)。 これとは逆に、水に溶いた片栗粉のように、強く回転を加えるとかえって抵抗を増す場合もあります(ダイラタンシー dilatancy)。 あるいはもっと動的な現象ですが、泥んこ遊びの時の泥のように、振り混ぜると抵抗力が減る場合もあります(チキソトロピー thixotropy)。
粘さといってもこのように単純ではありませんが、水やトルエンなど同種の粒子、あるいはあまり大きさの違わない分子の混合物からなる液体の場合には、おおむねニュートン流体としてふるまい、図の直線Aの勾配で粘さを評価できます。 液体の内部に注目すると、棒の回転速度 vθ を大きくすることは、液体の運動速度の距離による変動を大きくすることに相当します。 働く力は棒の表面積 S に比例しますから、液体の性質としての粘さは
![]()
という関係式(ニュートンの粘性法則)の比例係数 η で表現できることになります。 この比例係数 η を粘度(粘性率あるいは粘性係数)と呼びます。 またここでは流速の勾配に注目しましたが、物質輸送においては質量の流れが重要で、粘度を密度で割った動粘度(動粘性率あるいは動粘性係数)がよく用いられます。 動粘度の観点からは空気は水より粘い流体として振る舞います。
| 粘度(mPa s) | 動粘度(mm2 s-1) | |
| 水 | 0.891 | 0.891 |
| メタノール | 0.555 | 0.705 |
| エタノール | 1.078 | 1.373 |
| ヘキサン | 0.299 | 0.456 |
| シクロヘキサン | 0.898 | 1.160 |
| ベンゼン | 0.603 | 0.690 |
| 水銀 | 1.490 | 0.110 |
| グリセリン | 945 | 748 |
| 空気(300 K) | 0.0186 | 16.0 |
| 空気(400 K) | 0.0233 | 26.7 |
| 水蒸気(400 K) | 0.0133 | 24.3 |
水の粘度は 20 °Cで 1 mPa s、ガソリンなどはこの半分ぐらいの粘度になります。 またヘキサンとシクロヘキサンを比べると、粘度は3倍程度違います。 このような物質による粘度の違いを分子間力や分子構造から予測することは今日なお、非常に難しい問題です。
同様に一定圧力のもとで温度を上げると一般に液体の粘度は減少します。 この挙動は、日常生活の常識からは当然に見えますが、分子論的に見ると単純な現象ではありません。 空気、あるいは気体一般の粘度は温度を上げると大きくなるのです*。 このことは温度が上がり、分子運動が激しくなると速度の不均一さを均(なら)そうとする効果が大きくなるものとして理解できます。 分子運動の立場からは、むしろ温度を上げて粘度が減少することを説明するほうが難しいのです。 また一定体積の下で粘度の温度依存性を調べると、水やアルコールを除き、たいていの液体の粘度はほとんど温度依存性を示しません。 つまり温度を上げて粘度が小さくなるのは、ほとんど体積の熱膨張のためなのです。
| *気体の粘度が圧力に依存せず、また温度の上昇とともに増加することは、初期の分子運動論の重要な成果でした。 |
液体にさまざまな溶質が溶け込む過程は、濃度の不均一さが失われ均一になっていく過程、(広い意味での)拡散過程と見ることができます。 通常の溶液中の拡散過程は、たとえば棒でかき混ぜるような液体の巨視的な流れによる拡散(対流・分散)と、分子の運動による微視的なレベルでの拡散(狭い意味での拡散)とに大まかに分けることができます。
対流と(狭い意味での)拡散の違いは、ある地点からの溶質の拡散の速さを調べてみればはっきりします。 対流では時間に比例して遠方まで溶質が運ばれていくのに対し、(狭い意味での)拡散では、次の節で述べるように時間の平方根に比例して溶質が移動していくのです。 もし拡散速度を移動距離を移動時間で割ったもので定義したとすると、(狭い意味での)拡散では観測時間を長くするほど拡散速度は遅くなり、十分長く取ると0になってしまいます。 対流による拡散は重要ですが、溶質の個性とほぼ無関係に決まるので、化学では後者の拡散現象(分子拡散ということもあります)を主に扱います。
液体の中で分子は周りの分子と衝突してを繰り返しながら移動していきます。 仮に衝突の時間間隔をtCで一定とし、i番目の衝突との間に進む距離をqi (ベクトル)とすると、n回の衝突の間に進む距離xは、各回の衝突の間に進む距離の和をとればよいわけですから次の式のようになります:
![]()
この平均を取ってみると、衝突後進む向きはでたらめでしょうから 0 です。 つまり単純に平均すれば最初の位置にいるように見えるわけです。 けれどもこの2乗を取ってみると話は違ってきます(<W>というのはWの平均を意味します):
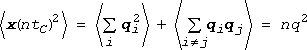
ここで衝突間に進む平均距離(平均自由行程といいます)を q としました。 つまり中心はもとの場所にあるのですが、その周りおよそ n1/2 q ぐらいの距離の範囲に分子がでたらめにばらついて存在しているということです。 この分子がもっぱら存在する領域の半径を r とすると、
![]()
という関係を得ます。 ここで平均自由行程 q に平均速度 v をかけたものを、定数 D の 6 倍とおきました(6 倍したのは3方向の成分を考慮したためです)。 この定数 D を拡散係数と呼びます。 拡散の速さ vD はこの半径 r の時間変化と考えられ、次の式のように時間の平方根に反比例して小さくなっていきます*。
![]()
* この式を信じれば観測時間を短くしていくと拡散速度が無限に速くなることになります。 実際には観測時間が分子間の衝突の時間程度になると、そもそもの拡散法則が成り立たなくなります。
| D / 10-9 m2 s-1 | |
| 窒素 | 1.88 |
| 酸素 | 2.10 |
| 二酸化炭素 | 1.92 |
| ベンゼン | 1.02 |
| ショ糖 | 0.523 |
| ヘモグロビン | 0.069 |
通常の溶質の場合、液体中の拡散係数はおよそ10-9 m2 s-1程度の値をとります。 さきに評価したように、分子の平均速度を 100 m/sとし約 0.01 nm程度進んではでたらめに向きを変えると考えると、ちょうどこの程度の拡散係数がえられます。
この拡散係数の値から大まかに 1 cmの距離を拡散する時間を見積もると 105 s、1日仕事になります。 深さが 10 cm ぐらいのマグカップに角砂糖をいれ、上から静かに水を注いだとすると、砂糖が溶けてコップの上の方まで拡散していくのに 100日以上かかるわけで、スプーンで混ぜるといった対流による(広い意味での)拡散が現実には非常に重要であることが分かるでしょう。
ここまではある地点に置かれた分子がどのように散らばっていくかを考えました。 同じような考えを、濃度の違う2つの容器AとBを細い管でつないだような場合にも適用することができます。
容器Aの濃度が c mol/m3、B の濃度を 0 とし、管の断面積をS m2、管の長さを L mとし、濃度が直線的に減るものとしましょう。すると A と B を結ぶ管の中で、ある分子が管の方向に沿ってqx mだけ進んでは、また方向を変えて運動するものとすれば、管のある断面をとると
AからB方向:(1/2) v S × [c + (1/2) qx (c /L)]
BからA方向:(1/2) v S × [c - (1/2) qx (c /L)]
だけの個数の分子の移動が起きるはずです。ですから正味の分子の流れは次の式で与えられることになります。
AからB方向に:(1/2) v S qx (c /L) = (1/2) qx v S (c /L) = D S (c /L)
つまり単位面積あたりの流速は、濃度の勾配 c/L に拡散係数をかけたもので与えられるというわけです(フィックの法則)。 ところでこの関係から海水(食塩 0.6 mol/L)の容器を真水の容器とを断面積 1 cm2、長さ 1 mのチューブでつないだとすると 1 時間かかって3×10-7 mol程度、 1 滴の海水のそのまた百分の1の食塩が拡散していくにすぎません(食塩の拡散係数はおよそ1.6×10-9 m2 s-1です)☆。
ある地点からだんだん拡がっていく場合、管を伝って濃度の低い方に流れていく場合、いずれの場合でも(狭い意味での)拡散はあまりに遅く、現実の拡散過程を考える上で無意味なもののように見えるかもしれません。 しかし微視的な環境では拡散は急速に進む過程です(たとえば 1 nm 程度の距離であれば、拡散は 1 ns のオーダーで起きる一方、速度の不均一さが距離 1 cmあたり10 m s-1 程度として対流では 1 ms オーダーかかります)。 またコップの中で角砂糖を溶かすような巨視的な場合、対流による液体の混合が速いので、角砂糖の表面付近での(狭い意味での)拡散は、それがもっとも遅い過程であるがために、全体の混合の速さを決める要因になってきます。
なお拡散係数はおおむね溶媒の粘度に逆比例することが知られています。 これは分子の移動に対する摩擦力が、溶媒の粘度に比例するものとして解釈できます。 けれども溶質分子の周りの環境が溶媒分子によって変化する効果なども働き、単純に溶媒の粘度だけでは説明できず、考慮すべき問題がたくさんあります。
煙突から出た煙が空気中に拡散していく現象は、一見狭い意味での拡散のように見えます。 けれどもこれは煙と空気の流れが複雑にない混ぜられた過程(分散 dispersion)です。 煙突から出た煙の分散は煙の成分の化学的性質にあまり依存しませんし、狭い意味での拡散から予想されるより千倍以上もの速さで拡散していきます。
分散でも(狭い意味での)拡散同様に、分子はある距離移動しては、またでたらめな方向に向かって運動していきます。 けれどもこれは個々の分子の運動ではなく、分子の集団としての運動、流体の乱れた流れ(乱流)によるものです。 分散でも拡散係数に相当する分散係数を考えることができますが、その評価の際には先の平均自由行程は大まかに言って流れの中にできる無数の渦の平均的なサイズ、速度は流速に対応することになります。 コーヒーカップの中の水をかき回すことを考えると、渦のサイズが数mm、流速は数十 cm/s でしょうか。 すると分散係数はおよそ 10-4 m2 s-1 になりますが、これは砂糖などの拡散係数の10万倍です。
よく水にインクを1滴垂らして、それが拡がっていくさまを(狭い意味での)拡散の例に出されることがあります。 けれどもこれはもっぱら分散によるもので、適切な例とは言えません。 拡散は溶液を作る際の最も基本的な過程といえるでしょうが、それを分子の成り立ちや分子間相互作用、分子運動と結び付けて議論するには、多くの物理的な問題を整理しておく必要があるのです。
☆ ここでの記述で拡散する食塩の量が2ケタ間違っていたので訂正しました。 誤りの指摘に感謝します。 2017.3.11