純粋な物質については、温度が決まると共存状態にある気体と液体の圧力・密度も決まります。 液体が気体になる時、分子間の引力的相互作用を断ち切るのにエネルギーが必要になります(蒸発熱。さらに詳細に見ると、これには膨張するのに必要なエネルギーも含まれていて「蒸発エンタルピー」という呼び方がされます)。 したがって温度を上げると、ルシャトリエの原理に従って、平衡は気体の側に移動し、蒸気圧は温度とともに指数関数的に大きくなっていきます。 たとえば 20 °C の水の場合、気体と液体の共存状態での圧力は 2.34 kPa(0.0231 atm)なので水温が 20 °C の場合水流ポンプで 2.34 kPa 以下の真空度は実現できません。 けれども水を 4 °C まで冷却すると蒸気圧は 0.81 kPa まで下がり、水流ポンプでも 1 kPa 以下の真空度が実現できるようになります。
液体というのは固体に比べて乱れた状態であり、気体は液体よりさらに乱れた状態であると考えることができます。 この乱れ具合を定量的に表すものさしとして、エントロピーという量があります。
ある粒子を1個体積 V の容器の中に導入することを考える時、エントロピー S の変化はその粒子の占める事のできる空間の体積を Va とすると、
![]()
で定義されます。 ここで <Va>0 は挿入する前に占めることができていた空間の体積の平均値を示し、理想気体であれば系の体積と等しいと置くことができます。 一般に対象とする系が乱れておれば挿入する粒子の占めることのできる体積は大きくなり、乱れが少なければ小さくなります。
|
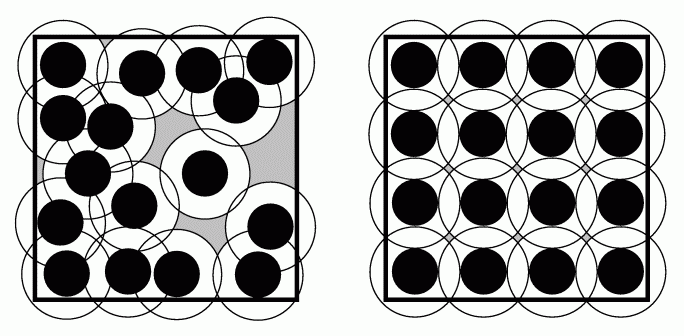
| 乱れた構造(左)と秩序だった構造(右)で、新たに導入される1個の粒子が占めることのできる領域(灰色の部分)は、乱れた構造の方が大きい。 |
ここでは体積について考えましたが、同じようなことを分子運動について考えることもできます。 温度を指定すれば、分子の速度分布は決まります。 全体として持つ運動エネルギーが大きいと、新たに挿入する分子1個が持ちうる運動エネルギーの範囲は大きくなります。 また分子の運動エネルギーが大きいほど、エネルギー的に不利な配置が実現できるようになり、より多くの状態が実現できるようになります。 このような考えからは、温度をエントロピーの増加量 ΔS に対するエネルギーの増分 ΔE の比として定義することもできます*。
![]()
*可逆過程ならばエネルギー変化は流入した熱量に等しいとおけ、物理化学の教科書にあるようにエントロピー変化は流入した熱量を温度で割ったものになります。あるいは圧力一定の条件下ならば、表式はエネルギーをエンタルピー E + PV で置き換えたものになります。
液体の蒸気圧が大気圧に等しくなる温度を標準沸点といいます。 水の標準沸点は 100 °Cです*。 標準沸点での蒸発にともなうエントロピーの変化 ΔSb は、蒸発熱 ΔEb を沸点の温度 Tb で割ったもので評価できます。
![]()
この標準沸点のエントロピー変化は、物質によらずおおよそ一定で約 90 J K-1 mol-1 程度の値をとることが知られていて、トルートン Trouton の通則と呼ばれます。 分子間の相互作用が大きく、蒸発に多くのエネルギーが必要な液体ほど沸点が高くなるのは、このトルートンの通則で説明されます。
*今日の温度目盛(ITS-90)で水の標準沸点は99.97 °Cです。
さて水中に水蒸気のみからなる気泡を発生させたとしましょう。水の蒸気圧が1気圧以下であれば大気圧に押しつぶされて気泡はつぶれてしまいます*。 一方、水の蒸気圧が1気圧以上になると気泡は大気圧に打ち勝って大きくなり、周りの液体の水から蒸発する水蒸気を取り込んでどんどん大きくなっていきます。 こうした現象が沸騰です。高い山に登ると大気圧が低下し、沸騰はより低温で起きるようになります。
*液温が沸点より低い時、容器の表面付近で沸点以上に加熱されてできた気泡は、液体の内部で冷却されつぶれてしまいます。これは表面沸騰(サブクールsubcooled沸騰)と呼ばれる現象で、古い鉄釜などで湯を沸かす時の音(茶の湯で「松風の音」(しょうふうのね)と言われるもの)は、この気泡の発生・消滅にともなうものです。
現実の沸騰は、気泡の生成や熱伝導などの要素が絡み合う複雑な現象です。 たとえば熱い鉄の板に水滴を落としても水滴が飛び跳ねるだけで、沸騰がただちに起きるわけではありません。 沸騰現象の複雑な仕掛けについては、抜山による有名な研究があります。 水を入れた容器の温度を上げていくと、最初核沸騰といわれる領域に達し次々と気泡が発生し、激しく沸騰がおきます。 けれどもさらに温度を上げると器壁が水蒸気で包まれ熱伝導が悪くなり(水蒸気の熱伝導度は水の 30 分の 1 程度)、水蒸気の膜を介した熱伝導が支配的な膜沸騰と呼ばれる沸騰に転じ、温度を上げると蒸発が逆に抑制されるようになります。 このような状況の下で、核沸騰の場合と同じように蒸気を発生させようと加熱を続けると、容器の融解・破損すらおきかねない事態になります。
|
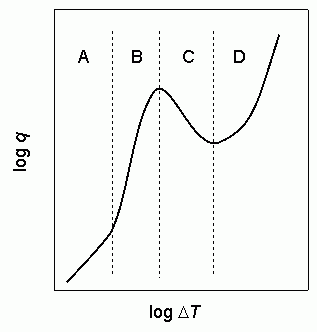
器壁の温度と液体の沸点の差ΔT を変えたときの、熱の流れ q の変化(沸騰曲線)。 最初は自然対流によって温度上昇とともに熱流が徐々に増加し(領域 A)、沸騰が始まって急速に熱流が増加する(核沸騰。領域 B)。 さらに器壁の温度を上げると蒸気膜ができ、かえって熱流は減少するようになり、温度を一定に保つのが困難な状況になる(遷移領域。領域 C)。 その後再び、温度の増加とともに熱流が増加する安定な領域に達する(膜沸騰。領域 D)。 両軸ともに対数スケールであることに注意。 典型的には水の場合、器壁の温度は領域 B と C の境界では 120 °C程度、C と D の境界は 200 °C程度以上になる。 |
気泡の発生も単純な過程ではありません。ガラス容器でアルカリ性の溶液を加熱するなど、器壁と液体が非常によく濡れている場合には気泡の発生が押さえられ、一端沸騰がおきると急激に気泡の拡大が起きて爆発的な沸騰(突沸)がおきます。 沸石を入れるのはこのような現象を防ぐためです。 通常の沸騰の場合でも、器壁の温度が液温より 10 °C 近く高いのは普通で、器壁付近の水は過熱状態(大気圧下で水は 300 °C 程度まで過熱可能であるとされます)にあります。
|
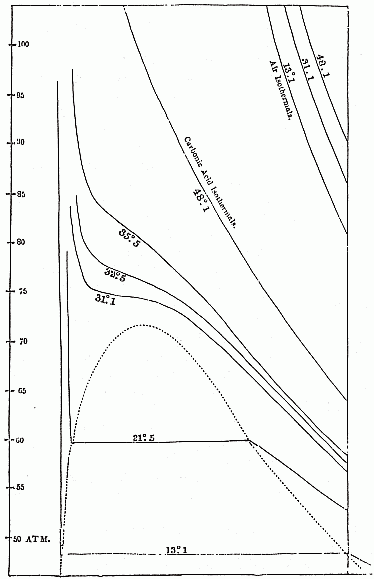
温度一定で二酸化炭素を圧縮・膨張させた際の圧力変化の様子(等温線)。 下方の6本が二酸化炭素の等温線で、上方の3本の等温線は空気の等温線。 点線は気液の共存線。 アンドリュースの実験結果(1872)をマックスウェルが書き直したもの(元の論文では横軸が圧力になっている)。 |
蒸気圧曲線を、温度-圧力ではなく、体積-圧力という観点から整理してみましょう。 温度が上がり蒸気圧が高くなるにしたがって、共存状態にある気相の比容(密度の逆数)は減り、液相の比容は増え、共存する気体と液体の比容の差は減少していきます。 そしてある温度、圧力に達すると両相の比容は等しくなり、それ以上温度・圧力を上げると気相と液相の共存状態は現れなくなります。 この気体と液体の区別が失われる気液の共存の限界の点を(気液の)臨界点と呼び、そこでの温度・圧力・密度をそれぞれ臨界温度・臨界圧力・臨界密度と呼びます。 図に示すのは二酸化炭素についての歴史的に著名な実験結果 を整理したもので、最下部の 13.1 °C の等温線では 47 atm 付近ではっきり見えている気液の共存状態が、 下から3番目の 31.1 °C の等温線では見られなくなってしまいます(今日的な測定によると二酸化炭素の臨界温度、臨界圧力は31.1 °C、73.0 atmで、よく一致しています)。
気体と液体が、臨界点以上の条件を介して連続的に移行できるということは、ある状況下の均一な流体を気体であるか液体であるかを見分けることが、たやすいことではないことをもの語っています。
2相が共存している状態では、気体と液体は容易に密度の大小で区別することができます。 しかし共存状態にない流体を、気体・液体に区別することは、別途「圧力一定で温度を上下する」(その時新たに出現した相の密度が元の相より高ければ、元の相は気体)といった「操作」を定義して初めて意味を持ちます。 下図に見る気体・液体の定義はボルツマンによるものですが、ボルツマンは「温度一定で圧力を上下する」という操作を基に、流体を「液体」(=圧力を下げると密度の低い相が出現)、「蒸気」(=圧力を上げると密度の高い相が出現)、「気体」(=圧力を上下しても一相のまま)の3つの領域に分類しました。 しかしボルツマン自身も指摘しているように、この分類は用いる操作に依存しています。 このことはまた「気体」「液体」の区別をする必要性の有無を問い掛けるものでもあります。
|
|
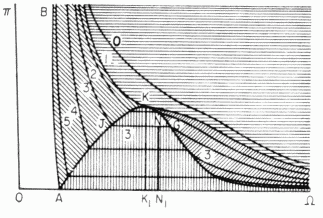
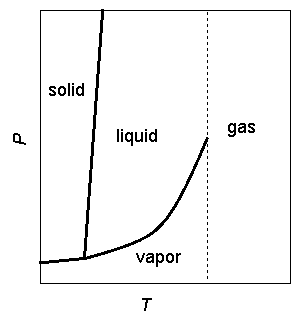
ボルツマンによる、流体の気体・蒸気・液体への分類。
左図はボルツマンが圧力(Π)-体積(Ω)図に示した流体の区分。
等温線 1 は臨界温度のもので、この等温線を境に上方が「気体」(横線でハッチがかかっている)、左下方が「液体」(左上から右下にハッチがかかっている)、
右下方が「蒸気」(右上から左下にハッチがかかっている)。
上下にハッチのかかっている領域は、気液の共存領域。 右図は左の圧力-体積図を温度-圧力図で示したもの。 臨界温度以上の領域が「気体」、臨界温度以下で圧力が蒸気圧以下の領域は「蒸気」、蒸気圧以上の領域が「液体」。 |